Bagaimana Jika Responden Survey di Kota Tertentu Sangat Sedikit Dibandingkan dengan Kota Lain?
Sebagai market researcher yang melakukan survey di berbagai kota atau bahkan negara dalam suatu region, beberapa kali saya kesulitan untuk merekrut responden sesuai dengan jumlah minimum target responden yang awalnya sudah didefinisikan.
Sebagai ilustrasi, misalkan saya sedang melakukan survey brand awareness di beberapa kota berikut ini:
| No | Kota | Minimum target responden |
|---|---|---|
| 1 | Jakarta | 300 |
| 2 | Bogor | 150 |
| 3 | Tangerang | 150 |
| 4 | Bekasi | 150 |
Sepanjang fieldwork hingga selesai, saya berhasil mendapatkan responden di Jakarta, Bogor, dan Tangerang dengan jumlah yang cukup dan mendekati target. Namun khusus di Kota Bekasi, saya hanya mendapatkan 14 orang responden saja.
Misalkan berikut adalah perhitungan berapa banyak responden yang aware terhadap brand:
| No | Kota | Minimum Target Responden | Responden Didapatkan | Responden yang Aware | Persentase Awareness |
|---|---|---|---|---|---|
| 1 | Jakarta | 300 | 300 | 57 | 19% |
| 2 | Bogor | 150 | 140 | 20 | 14.3% |
| 3 | Tangerang | 150 | 137 | 16 | 11.7% |
| 4 | Bekasi | 150 | 14 | 0 | 0 |
| TOTAL | 650 | 591 | 93 | 15.7% |
Kemudian setelah dicek, ternyata dari 14 responden di Kota Bekasi tersebut tidak ada satupun yang aware brand yang sedang disurvey. Jika saya pakai perhitungan biasa, kesimpulannya:
Ada indikasi bahwa brand awareness di Kota Bekasi adalah 0%.
Apakah ini masuk akal? Belum tentu.
Bisa jadi sebenarnya ada warga Bekasi yang aware tapi saya cuma apes saja mengambil sampel 14 orang yang tidak aware. Menyimpulkan 0% (atau sebaliknya 100%) dari data yang sangat sedikit itu berbahaya.
Nah, kali ini saya akan menggunakan Hierarchical Bayesian Model (HBM) untuk memberikan alternatif analisa pada kejadian seperti ini.
Konsep: Meminjam Kekuatan (Borrowing Strength)
Secara intuitif, HBM bekerja dengan prinsip kompromi. Perhatikan beberapa alternatif berikut ini:
- Pendekatan Naif (No Pooling): Kita percaya penuh pada data tiap kota. Kalau data Kota Bekasi mengatakan bahwa awareness 0%, maka benar-benar 0%. (Risiko: Overfitting pada sampel kecil).
- Pendekatan Global (Complete Pooling): Kita tidak peduli kota, kita pukul rata pakai angka Nasional (total). Kalau total 15.7%, maka Kota Bekasi dianggap 15.7% juga. (Risiko: Mengabaikan karakteristik lokal).
- Hierarchical Bayes (Partial Pooling): Jalan tengahnya dengan
cara:
- Jika data kota tersebut banyak (seperti Jakarta), model akan percaya pada data kota itu.
- Jika data kota tersebut sedikit (seperti Kota Bekasi), model akan “ragu” dan menarik angkanya mendekati rata-rata total.
Inilah yang disebut shrinkage. Data yang tidak pasti “ditarik” ke arah group mean (total) untuk mendapatkan estimasi yang lebih robust. Kita “meminjam kekuatan” statistik dari data total untuk memperbaiki estimasi di level kota yang datanya sedikit.
Sekarang saya akan hitung dan simulasikan HBM menggunakan R untuk melihat brand awareness di Kota Bekasi berapa nilainya.
Simulasi dengan R
Saya akan gunakan library rstanarm yang memudahkan dalam membuat
model Bayesian.
1. Siapkan Data
# Setting seed biar reproducible
set.seed(10104074)
# Kita buat data agregat dulu
data_simulasi <- tibble(
kota = c("Jakarta", "Bogor","Tangerang", "Bekasi"),
n_responden = c(300,140,137,14),
n_aware = c(57,20,16,0)
) %>%
mutate(
raw_awareness = n_aware / n_responden
)
print(data_simulasi)
# A tibble: 4 × 4
kota n_responden n_aware raw_awareness
<chr> <dbl> <dbl> <dbl>
1 Jakarta 300 57 0.19
2 Bogor 140 20 0.143
3 Tangerang 137 16 0.117
4 Bekasi 14 0 0
2. Membentuk Data untuk Model
Model stan_glmer (Generalized Linear Mixed Model versi Bayesian)
membutuhkan data per baris responden (0 atau 1) untuk awareness. Kita
expand data di atas.
# Expand data menjadi per responden (row-level data)
data_long <- data_simulasi %>%
uncount(n_responden, .id = "id") %>%
group_by(kota) %>%
mutate(
is_aware = ifelse(row_number() <= n_aware[1], 1, 0)
) %>%
ungroup()
# Cek struktur data
glimpse(data_long)
Rows: 591
Columns: 5
$ kota <chr> "Jakarta", "Jakarta", "Jakarta", "Jakarta", "Jakarta", "…
$ n_aware <dbl> 57, 57, 57, 57, 57, 57, 57, 57, 57, 57, 57, 57, 57, 57, …
$ raw_awareness <dbl> 0.19, 0.19, 0.19, 0.19, 0.19, 0.19, 0.19, 0.19, 0.19, 0.…
$ id <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 1…
$ is_aware <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
3. Modelling dengan Hierarchical Bayes
Di sini kita menggunakan formula (1 | kota). Artinya: Setiap kota
punya intercept (tingkat awareness) sendiri-sendiri, tapi mereka
berasal dari distribusi populasi yang sama (Normal Distribution).
# Fitting model Bayesian
# family = binomial karena outcome-nya 0 atau 1 (Bernoulli)
model_hbm <- stan_glmer(
is_aware ~ (1 | kota),
data = data_long,
family = binomial(link = "logit"),
prior = normal(0, 2.5), # Prior standar yang weakly informative
prior_intercept = normal(0, 2.5),
chains = 4, iter = 2000, seed = 10104074,
refresh = 0
)
# Melihat ringkasan hasil
summary(model_hbm)
Model Info:
function: stan_glmer
family: binomial [logit]
formula: is_aware ~ (1 | kota)
algorithm: sampling
sample: 4000 (posterior sample size)
priors: see help('prior_summary')
observations: 591
groups: kota (4)
Estimates:
mean sd 10% 50% 90%
(Intercept) -1.9 0.4 -2.4 -1.8 -1.5
b[(Intercept) kota:Bekasi] -0.4 0.7 -1.3 -0.2 0.1
b[(Intercept) kota:Bogor] 0.1 0.5 -0.3 0.0 0.6
b[(Intercept) kota:Jakarta] 0.4 0.5 0.0 0.3 0.9
b[(Intercept) kota:Tangerang] -0.1 0.5 -0.5 -0.1 0.4
Sigma[kota:(Intercept),(Intercept)] 0.6 1.1 0.0 0.2 1.5
Fit Diagnostics:
mean sd 10% 50% 90%
mean_PPD 0.2 0.0 0.1 0.2 0.2
The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).
MCMC diagnostics
mcse Rhat n_eff
(Intercept) 0.0 1.0 225
b[(Intercept) kota:Bekasi] 0.0 1.0 1068
b[(Intercept) kota:Bogor] 0.0 1.0 271
b[(Intercept) kota:Jakarta] 0.0 1.0 218
b[(Intercept) kota:Tangerang] 0.0 1.0 291
Sigma[kota:(Intercept),(Intercept)] 0.1 1.0 350
mean_PPD 0.0 1.0 4013
log-posterior 0.1 1.0 938
For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).
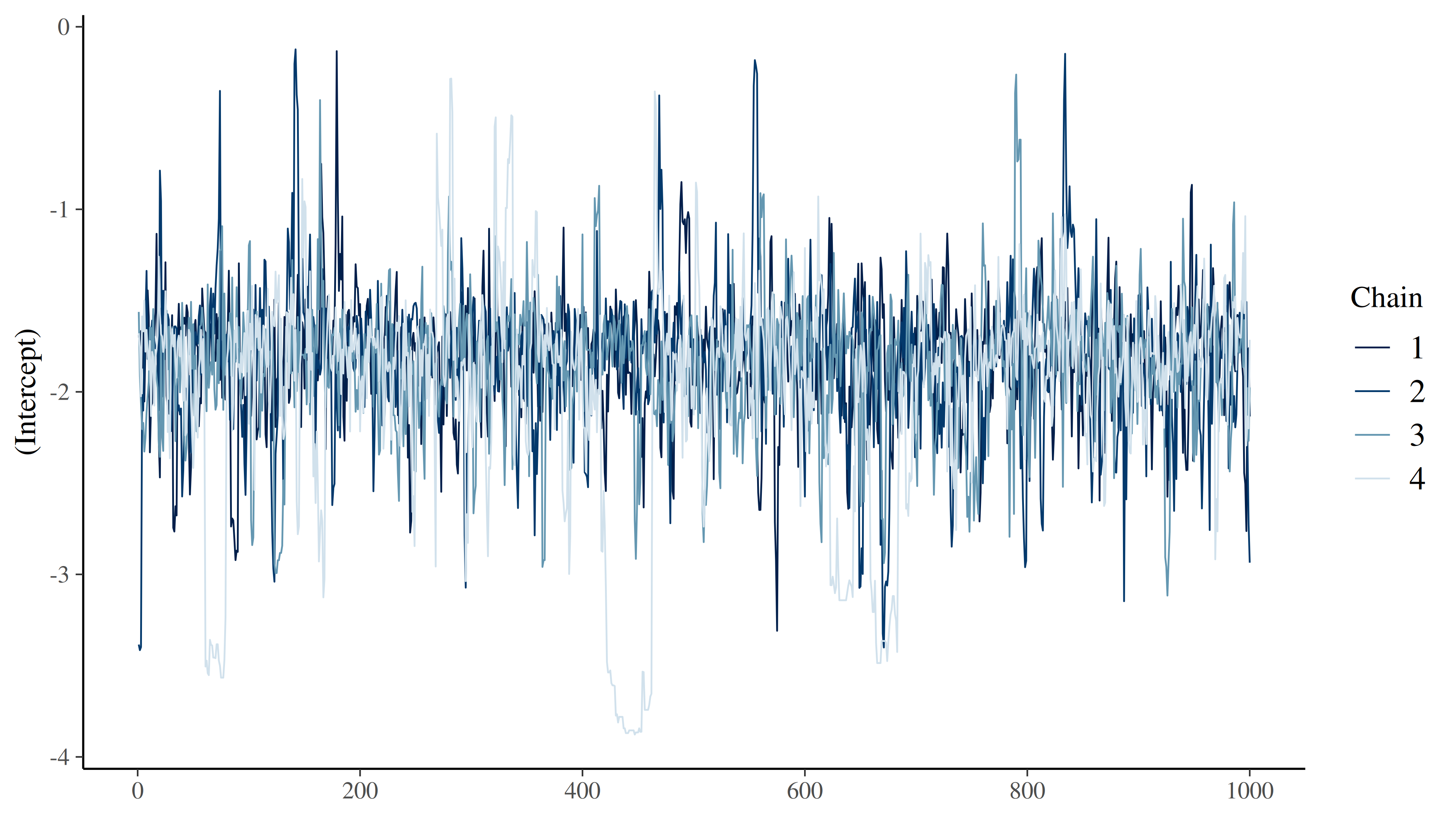
Model yang dihasilkan sudah baik. Bisa dilihat dari:
- Nilai kolom Rhat yang berkisar antara 1.0 - 1.05.
- Rhat merupakan indikator apakah rantai simulasi (chains) sudah “sepakat” atau konvergen.
- Cek Traceplot: Kita perlu melihat visualisasi pergerakan sampling-nya. Kita ingin melihat grafik yang acak dan tercampur sempurna, bukan grafik yang punya pola naik-turun lambat.
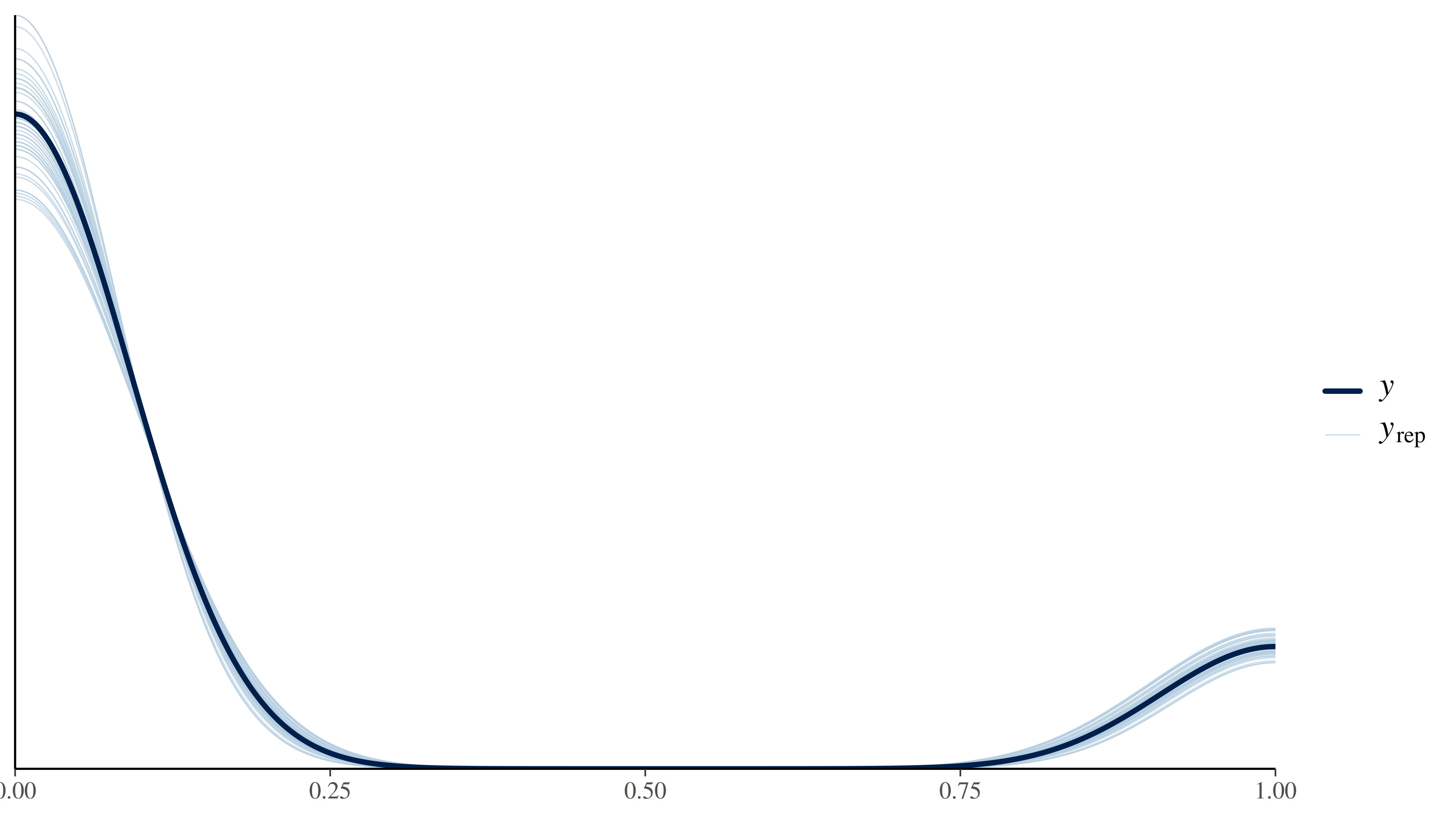
- Posterior Predictive Check (PPC): Kalau model ini baik maka model bisa membuat data simulasi yang mirip dengan data asli.”
[1] "Traceplot"
[1] "Posterior Predictive Check"
4. Membandingkan Hasil: Raw vs Bayesian
Sekarang, mari kita ambil hasil estimasi dari model Bayesian (Posterior Mean) dan bandingkan dengan hitungan manual biasa.
# Ambil fitted values (probabilitas)
# Kita ambil rata-rata posterior untuk tiap kota
hasil_bayes <- data_long %>%
mutate(pred_bayes = fitted(model_hbm)) %>%
group_by(kota) %>%
summarise(
bayes_awareness = mean(pred_bayes)
)
# Gabungkan dengan hitungan manual
final_comparison <- data_simulasi %>%
left_join(hasil_bayes, by = "kota") %>%
select(kota, n_responden, raw_awareness, bayes_awareness) %>%
mutate(
raw_perc = scales::percent(raw_awareness, accuracy = 0.1),
bayes_perc = scales::percent(bayes_awareness, accuracy = 0.1),
diff = bayes_awareness - raw_awareness
)
| kota | persen_real | persen_bayes | perbedaan |
|---|---|---|---|
| Jakarta | 19.0% | 17.7% | -1.25% |
| Bogor | 14.3% | 14.3% | -0.02% |
| Tangerang | 11.7% | 13.2% | 1.47% |
| Bekasi | 0.0% | 11.6% | 11.58% |
Apa yang Terjadi?
Kita bisa melihat bahwa di Jakarta, Bogor, dan Tangerang angka persentase brand awareness versi Bayesian sudah mendekati nilai persentase real-nya. Sedangkan angka persentase brand awareness di Kota Bekasi naik menjadi sekitar 11%.
Inilah yang disebut dengan shrinkage.
Model “berpikir”:
“Oke, di Kota Bekasi datanya mengatakan 0% yang hanya berasal dari 14 orang. Sedangkan rata-rata total (Jakarta, Bogor, dan Tangerang) itu sekitar 15.7%. Tak mungkin *awareness di Kota Bekasi benar-benar 0%. Sepertinya surveyor belum ketemu responden orang yang aware saja. Maka dari itu model akan menggeser angkanya mendekati rata-rata total tapi tak sampai 15.7% juga.”*
Estimasi 11% ini jauh lebih aman dan masuk akal secara statistik daripada kita menelan mentah-mentah angka 0%.
Kapan Harus Menggunakan HBM?
Metode Hierarchical Bayes ini sangat powerful digunakan saat:
- Market Research Multi-Area: Terutama jika budget survey tidak merata di semua kota.
- Analisa Performa Salesman: Jangan buru-buru memecat sales baru yang konversinya 0% padahal dia baru prospek ke 3 orang.
- AB Testing: Ketika trafik di varian B masih sangat sedikit.
Analisa Bayesian bukan cuma soal rumus yang rumit, tapi soal bagaimana kita memasukkan “common sense” (bahwa area-area ini punya kemiripan) ke dalam model matematika.
if you find this article helpful, support this blog by clicking the ads.
