Materi Training: Belajar Regresi Linear yang Proper dengan R

Sudah beberapa kali saya menuliskan mengenai penggunaan analisa regresi linear dalam pekerjaan sehari-hari. Tapi ternyata saya baru sadar ternyata saya belum pernah menuliskan mengenai pengujian asumsi secara proper.

Menggunakan data yang pernah saya tulis mengenai kebahagiaan dan GDP suatu negara, saya akan menguji asumsi dari model regresi linear yang ada tersebut.

Membuat Model Regresi

Pertama-tama, saya akan buat model regresi dari variabel gdp dan life.satisfaction sebagai berikut:

## 
## Call:
## lm(formula = life.satisfaction ~ gdp.per.capita, data = data)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.06541 -0.50551  0.00623  0.55957  1.90277 
## 
## Coefficients:
##                 Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    4.649e+00  9.235e-02   50.34   <2e-16 ***
## gdp.per.capita 4.338e-05  3.430e-06   12.65   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.7673 on 140 degrees of freedom
## Multiple R-squared:  0.5333, Adjusted R-squared:   0.53 
## F-statistic:   160 on 1 and 140 DF,  p-value: < 2.2e-16

Formula regresinya:

Goodness of fit dari model

Sebelum lebih jauh, saya akan cek dulu parameter goodness of fit dari model berupa:

1. R-Squared
2. p-value
3. Mean Squared Error (MSE)

R-Squared

Dari nilai tersebut, model regresinya dinilai so-so.

p-value

Nilai p-value sebesar .

Model menunjukkan pengaruh signifikan dari variabel prediktor terhadap variabel target.

Mean Squared Error

MSE(model$fitted.values,data$life.satisfaction)

## [1] 0.5805273

---

Uji Asumsi

Sekarang saya akan melakukan uji asumsi dari model regresi linear yang telah dibuat. Jika semuanya terpenuhi, maka model tersebut sudah bagus.

Normality of Residual

Pertama-tama, saya akan mengecek apakah error-nya berdistribusi normal atau tidak.

Uji hipotesis:

• : residual berdistribusi normal.
• : residual tidak berdistribusi normal.
• Jika , tolak .

Saya lihat dulu histogramnya sebagai berikut:

hist(model$residuals)

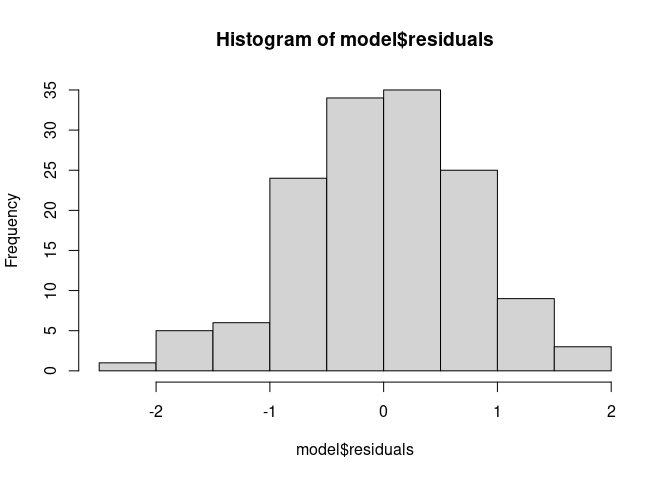
Sekarang saya lakukan uji kenormalan dengan uji shapiro.test():

shapiro.test(model$residuals)

## 
##  Shapiro-Wilk normality test
## 
## data:  model$residuals
## W = 0.99168, p-value = 0.5714

Kesimpulan :

Residual dari model regresi linear berdistribusi normal.

Linearity Check

Saya bisa cek linearity dengan plot berikut:

# melihat plot residual dan fitted values dari model
plot(model,1)

Uji hipotesis:

• : tidak linear.
• : linear.
• Jika , tolak .

Saya akan lakukan uji korelasi menggunakan cor.test() untuk variabel prediktor:

cor.test(data$gdp.per.capita,data$life.satisfaction)

## 
##  Pearson's product-moment correlation
## 
## data:  data$gdp.per.capita and data$life.satisfaction
## t = 12.648, df = 140, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.6428813 0.7988961
## sample estimates:
##       cor 
## 0.7302727

Kesimpulan:

Lolos uji linearity!

Uji Homoscedascity

Apa maksud dari homoscedasticity? Artinya error tidak memiliki pola. Sedangkan jika heteroscedasticity artinya error-nya berpola. Kalau terdapat heteroscedasticity, kemungkinan ada outlier yang harus dibuang.

Uji hipotesis:

• : model homoscedasticity.
• : model heteroscedasticity.
• Jika , tolak .

Plot error dan nilai aktualnya:

plot(model$residuals,data$life.satisfaction)

Uji statistiknya dengan function bptest() dari library(lmtest).

bptest(model)

## 
##  studentized Breusch-Pagan test
## 
## data:  model
## BP = 2.5056, df = 1, p-value = 0.1134

Kesimpulan:

Lolos uji homoscedasticity!

Uji Multicollinearity

Nah, uji yang ini baru bisa akan kita lakukan jika kita melakukan multiple linear regression, yakni saat variabel prediktornya lebih dari satu. Kita tidak mau kalau variabel prediktor di model kita itu saling berpengaruh (dependen).

Untuk melakukannya, kita perlu mengujinya menggunakan nilai vif.

Cek dengan fungsi vif() dari library(car) untuk mengetahui variabel-variabel mana yang tidak bisa ditoleransi menjadi sebuah prediktor.

# vif(model)

Nilai vif yang baik harus . Ketika , maka harus ada variabel yang dieliminasi atau dilakukan feature engineering (membuat variabel baru dari variabel-variabel yang ada).

---

Kesimpulan

Model yang saya buat ternyata lolos semua uji asumsi. Artinya model ini sudah cukup bagus. Kita tinggal menimbang angka-angka parameter goodness of fit dari model untuk menentukan apakah model ini sudah cukup baik dalam membuat prediksi gdp terhadap life satisfaction dari suatu negara.