Bunch of Ideas, a little bit of Maths.

I am mathematician doing market research and data science

12 minute read

Prolog

Sudah beberapa bulan ini, saya dan beberapa teman-teman alumni Matematika sedang membentuk komunitas bersama dengan para mahasiswa Matematika ITB tingkat 2 dan 3. Tujuan kami alumni adalah untuk grooming para mahasiswa agar siap pakai setelah lulus dalam bidang data science.

Dari kami alumni sendiri, bidang pekerjaannya cukup beragam. Ada yang dari FMCG, retail, telco, banking, sampai start up market place.

Salah satu keuntungan bagi saya dalam sharing dan mengajar di komunitas ini adalah saya gak harus menjelaskan secara detail kepada mereka. Kenapa?

Mereka kan mahasiswa matematika. Justru secara skill bisa jadi mereka lebih jago daripada saya dan teman-teman alumni lainnya.

Kami tinggal memoles di bagian softskill dan membuka wawasan terhadap algoritma-algoritma dan teknik yang biasa dipakai di berbagai bidang industri.

Competition

Beberapa waktu yang lalu, salah satu senior saya yang sekarang bekerja di salah satu marketplace memberikan satu dataset untuk dikompetisikan.

Kali ini kompetisinya bukan tentang prediction atau classification! Justru harus diselesaikan dengan teknik yang kita sudah pelajari sejak SMA. Apa itu? Linear Programming.

Saya sudah menuliskan tentang aplikasi linear programming di tulisan sebelumnya. Tapi kali ini teknik yang digunakan sedikit berbeda.

Problem Statement

Ceritanya, senior saya memiliki data 7000an produk yang dijual di marketplace-nya. Produk-produk tersebut adalah produk yang memiliki price elasticity yang tinggi.

Jadi, saat ada diskon potongan harga di produk tersebut, sales qty-nya akan meningkat.

Semakin bagus jualan produk tersebut tentunya juga akan menambah profit dari marketplace tersebut!

Diskon potongan harga bisa diberikan oleh si seller atau dari pihak marketplace. Bisa saja dua-duanya (baik seller dan marketplace) memberikan diskon terhadap produk tersebut.

Coba deh diingat saat kita berbelanja di marketplace, apa kita pernah mendapatkan diskon potongan harga double? Potongan dari seller dan kupon yang diberikan marketplace.

Dia diberikan budget sebesar Rp 200.000.000 untuk melakukan promo. Kini dia harus memilih sebanyak-banyaknya produk yang bisa digelontorkan promo diskon. Tujuannya simpel: gain the highest profit dari produk-produk pilihan tersebut.

Kompetisi: Produk apa saja yang harus dipilih?

Dataset

Berikut adalah cuplikan dataset yang digunakan:

## 10 Data Teratas
product_code cost expected_profit
6000227-0001 22950 -8338.50
6000094-0002 240 112.80
6000100-0003 70350 78289.50
6000301-0004 15300 7191.00
6000307-0005 2700 2079.00
6000324-0006 19800 -10494.00
6000348-0007 50460 55036.20
6000370-0008 52110 -1563.30
6000377-0009 24300 -8829.00
6000378-0010 1425 1097.25

Ada tiga variabel yang digunakan, yakni:

  1. product_code, yakni kode product yang listed di marketplace. Sebenarnya nama brand dan deskripsi produk ada. Tapi saya hide saja yah v(n_n).
  2. cost, yakni biaya yang harus dikeluarkan untuk memberikan potongan diskon kepada pelanggan. Ini adalah variabel yang harus diperhatikan, karena apapun produk yang dipilih nanti, \sum(cost_i) \leq Rp200jt.
  3. expected_profit, yakni profit yang diproyeksikan akan didapatkan marketplace saat produk diberikan diskon. Nah, untuk menghitung berapa besar expected_profit per produk ada caranya tersendiri. Kelak, perhitungan ini akan dijadikan kompetisi tahap kedua.

Solusi

Sebagaimana yang telah saya sampaikan di tulisan sebelumnya, kini saya akan selesaikan permasalahan ini dengan dua cara:

  1. Cara probabilistik: Simulasi Monte Carlo, dan
  2. Cara eksak: Binary Linear Programming.

Tapi sebelum saya masuk ke cara penyelesaian, saya akan lakukan pemilahan dataset terlebih dahulu.

Total ada 7617 baris data TAPI tidak semua data akan saya gunakan. Saya hanya akan menggunakan produk-produk yang memiliki expected_profit > 0.

## Framework Pemilahan Data

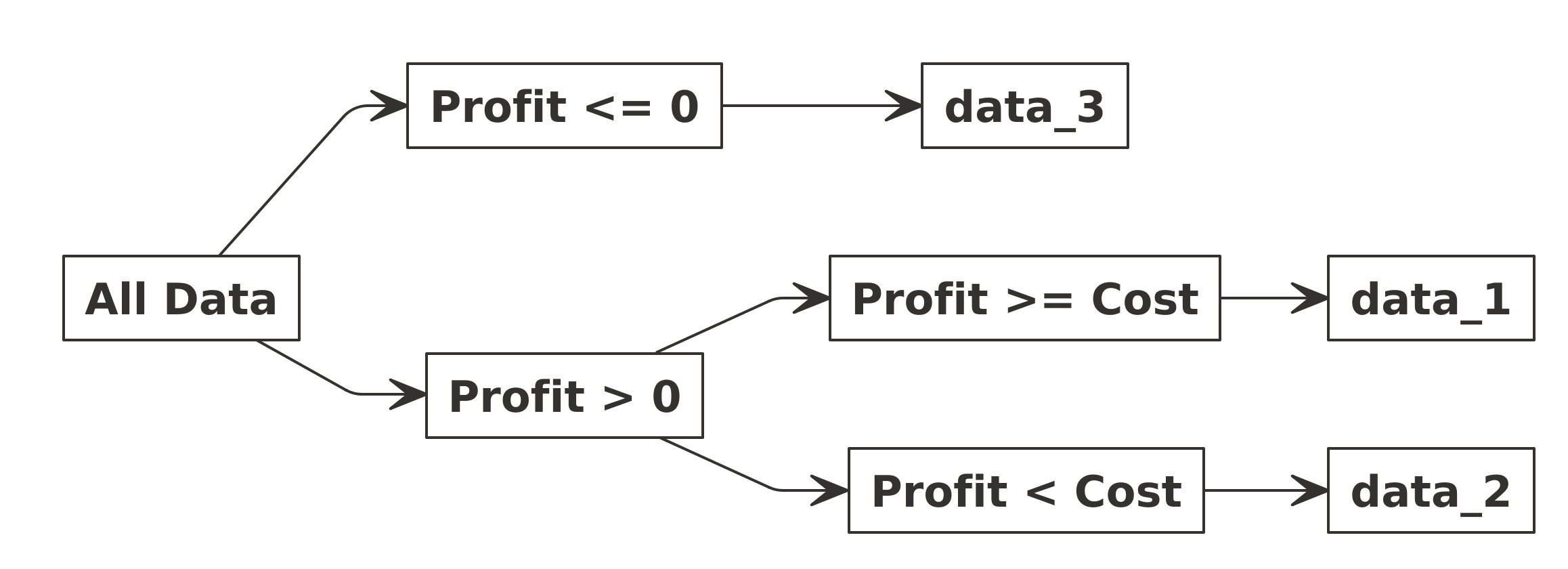
Setelah saya cek, ada tiga data yang saya dapatkan, yakni:

  1. data_1, berisi 626 baris data.
  2. data_2, berisi 1327 baris data.
  3. data_3, berisi 5664 baris data. Saya tidak akan memilih dataset ini karena bukan profit yang didapatkan tapi malah rugi.

data_1

Kalau saya hitung, saya dapatkan expectedprofit dari data_1 sebesar 146862305.4135 dan cost sebesar 90442848.93.

Karena saya dapatkan total cost masih di bawah Rp 200 jt, maka saya akan gunakan semua produk pada data_1 ini.

data_2

Sekarang saya tinggal memilih produk-produk apa saja yang harus dimasukkan dari dataset ini.

Formulasi matematika dari kondisi ini adalah:

Constraint Cost

\sum(cost_{data2}) \leq 200.000.000 - \sum(cost_{data1})

\sum(cost_{data2}) \leq 109.557.151

Karena data_2 memiliki 1327 baris produk, maka saya tulis sebagai berikut:

cost_1*x_1 + cost_2*x_2 + ... + cost_n*x_n + ... + cost_{1327}*x_{1327} \leq 109.557.151

Dengan nilai x_1,x_2,...,x_n,x_{1327} berupa bilangan binary {0,1}.

  • 0 berarti produk tidak dipilih.
  • 1 berarti produk dipilih.

Objective Function

Tujuan saya adalah memaksimalkan expected_profit.

MAX (\sum(profit_{data2}))
Karena data_2 memiliki 1327 baris produk, maka saya tulis sebagai berikut:

MAX (profit_1*x_1 + profit_2*x_2 + ... + profit_n*x_n + ... + profit_{1327}*x_{1327})
Dengan nilai x_1,x_2,...,x_n,x_{1327} berupa bilangan binary {0,1}.

  • 0 berarti produk tidak dipilih.
  • 1 berarti produk dipilih.

Solusi

Simulasi Monte Carlo

Ini adalah cara pertama yang terpikir oleh saya saat pertama kali mendapatkan problem seperti ini. Saya tidak akan mencari solusinya secara brute force (mencoba-coba semua kombinasi yang mungkin dari 1327 produk).

Kenapa?

Secara algoritma memang mudah untuk membuat semua kombinasi yang mungkin. Tapi secara komputasi pasti melakukan ini butuh waktu yang lama.

Oleh karena itu, alih-alih mencoba semua kombinasi, saya hanya akan generate a large finite of random numbers untuk melakukan simulasi kombinasi yang mungkin muncul dari data_2 yang memenuhi constraint cost dan objective function.

Biar gak kelamaan, saya akan set di 5000 iterasi saja. Berapa lama prosesnya? Berapa max expected profit yang saya dapatkan?

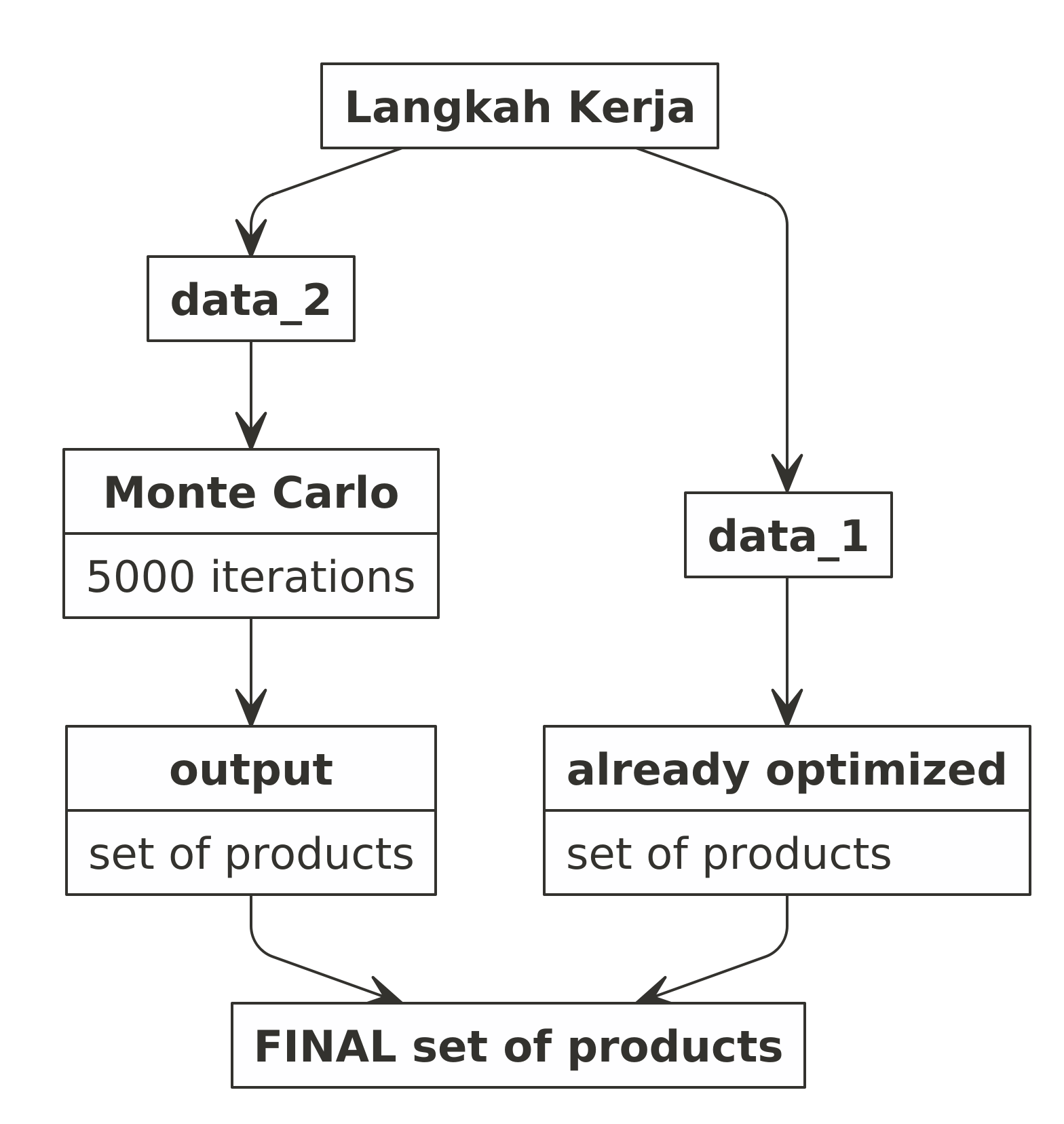
## Proses iterasi memakan waktu selama: : 30.367 sec elapsed

## FINAL FINDINGS: set of products

##   Banyak produk Total cost Total expected profit
## 1          1443  199184676             198446992

Tentunya dengan menambah banyaknya iterasi, saya menduga total expected profit-nya bisa lebih besar karena bisa jadi saya mendapatkan kombinasi produk yang lebih baik.

Binary Linear Programming

Sekarang saya akan mencoba cara kedua, yakni dengan salah satu cabang linear programming. Kalau saya perhatikan kembali, jawaban dari persamaan constraint cost dan objective function, yakni (x_1,x_2,...,x_n,...,x_{1327}) hanya memiliki jawaban biner 0 atau 1.

Maka, saya akan gunakan binary linear programming untuk mencari solusinya menggunakan library(lpSolve) di R.

## Proses solving memakan waktu selama: : 25.361 sec elapsed

## FINAL FINDINGS: set of products

## # A tibble: 1 x 3
##   `Banyak produk` `Total cost` `Total expected profit`
##             <int>        <dbl>                   <dbl>
## 1            1599   199999992.              205709825.

SUMMARY

  • Cara perhitungan eksak memberikan hasil yang lebih baik dan tinggi dibandingkan cara probabilistik pada kasus ini. Tapi jika tidak ada constraint pada waktu komputasi, membuat algoritma Monte Carlo lebih mudah bagi saya.
  • Binary linear programming bisa digunakan untuk berbagai macam masalah real, seperti pemilihan portofolio saham, alokasi karyawan, dan sebagainya.

You May Also Enjoy

Geocoding di R Menggunakan tidygeocoder

7 minute read

Di blog ini saya sudah menuliskan berbagai macam metode dan teknik pengambilan data longlat dari alamat (vice versa). Istilah kerennya itu geocoding.