Menyelesaikan Masalah Bisnis Terkait Peluang Menggunakan Distribusi Binomial

Pendahuluan

Beberapa minggu yang lalu, saya sempat mengikuti diskusi antara tim sales dan tim digital marketing dari suatu perusahaan (bukan perusahaan tempat saya bekerja saat ini yah). Salah satu bahasan dari diskusi tersebut adalah bagaimana tim sales (dengan segala keterbatasannya) bisa membuktikan klaim dari tim digital marketing. Lantas apa klaimnya?

Tim digital marketing mengklaim:

Sebanyak 70% pembeli produk mereka di modern outlet diakibatkan oleh iklan yang mereka buat.

Oleh karena tim sales tidak memiliki sumber daya untuk melakukan market research, mereka hanya mampu mengerahkan sales promotion girl untuk melakukan survey singkat di beberapa modern outlet di suatu time window tertentu.

Menggunakan prinsip rule of five:

The rule of five is a rule of thumb in statistics that estimates the median of a population by choosing a random sample of five from that population. It states that there is a 93.75% chance that the median value of a population is between the smallest and largest values in any random sample of five. This rule can be used to save data collection time in order to make a quicker business decision.

Tim sales melakukan survey singkat dari sepuluh modern outlet. Tim SPG akan mewawancarai lima orang pembeli pertama yang ada untuk kemudian ditanyakan “apakah mereka membeli karena iklan digital?”. Akhirnya didapatkan data sebanyak 50 orang responden yang didapatkan dari sepuluh buah modern outlet (lima responden per modern outlet).

Berikut adalah data yang didapatkan tim sales:

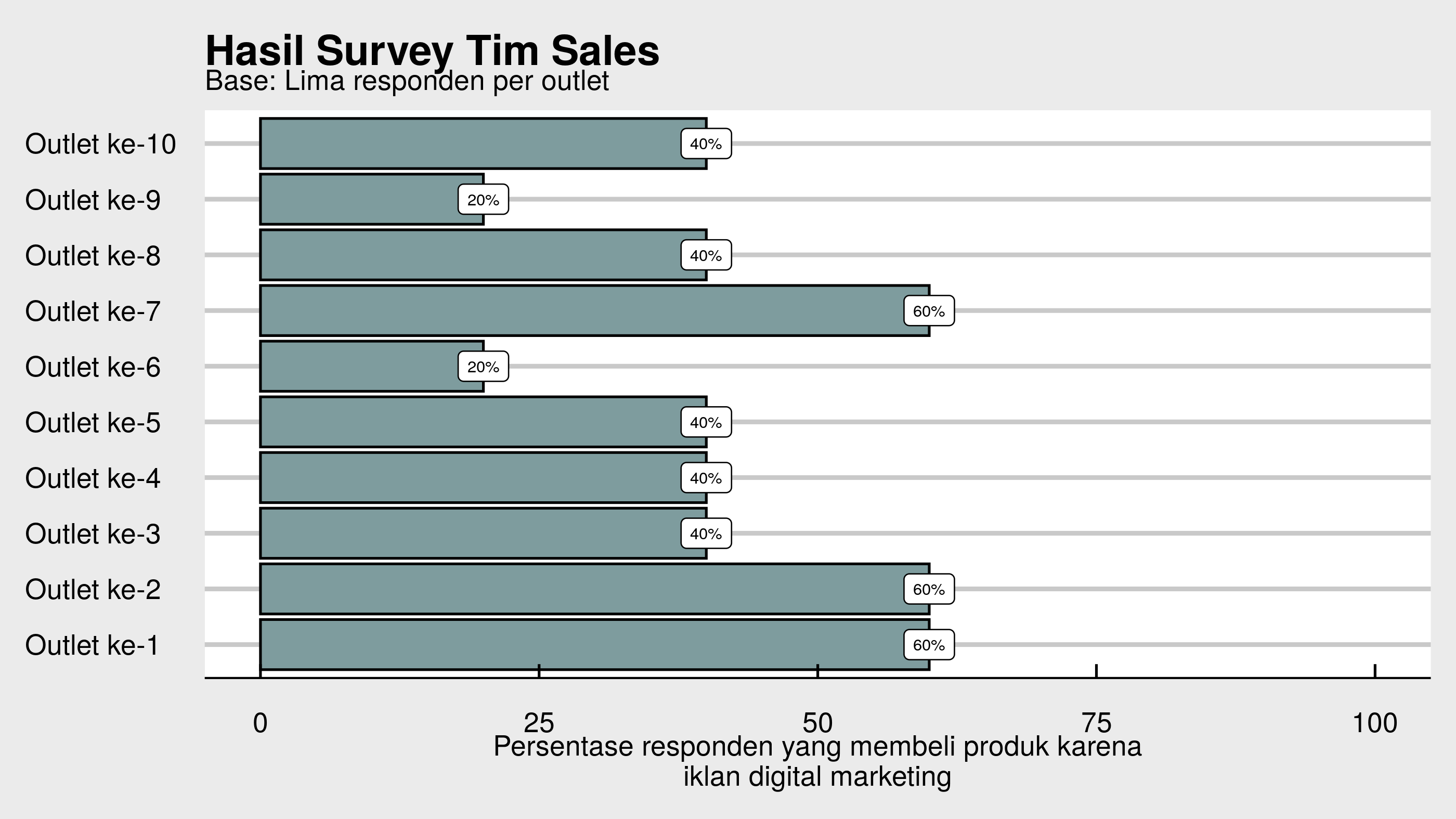
Rata-rata persentasenya adalah 42%. Secara total kita dapatkan 21 orang yang membeli produk karena iklan dari total 50 orang responden.

Pertanyaannya

Bagaimana menentukan benar/tidaknya klaim tim digital marketing dari data seadanya tim sales?

---

Penyelesaian

Mendapatkan business question seperti itu membuat saya berpikir berulang kali bagaimana penyelesaiannya. Sempat saya berpikir untuk menggunakan prinsip simulasi Monte Carlo seperti tulisan saya terkait COVID dulu. Namun kali ini saya akan mencoba menyelesaikannya dengan cara yang lebih eksak.

Distribusi Binomial

Pikiran saya terbang jauh saat saya sedang kuliah analisa data dulu pada materi distribusi binomial. Distribusi binomial adalah distribusi peluang dari variabel diskrit; biasa digunakan untuk menyelesaikan masalah-masalah yang bisa dikategorikan sebagai success atau not success yang saling bebas. Setiap hasil percobaan memiliki probabilitas .

Distribusi ini sering kali digunakan untuk memodelkan jumlah keberhasilan pada jumlah sampel dari jumlah populasi . Secara matematis, peluang bisa dihitung dari formula berikut:

Dimana:

• merupakan kombinasi terjadinya event kali dari total kejadian.
• menandakan proporsi success pada populasi.

Pada kasus yang saya hadapi, bisa saya definisikan dan = 21. Jika saya buat grafik distribusi kumulatif-nya:

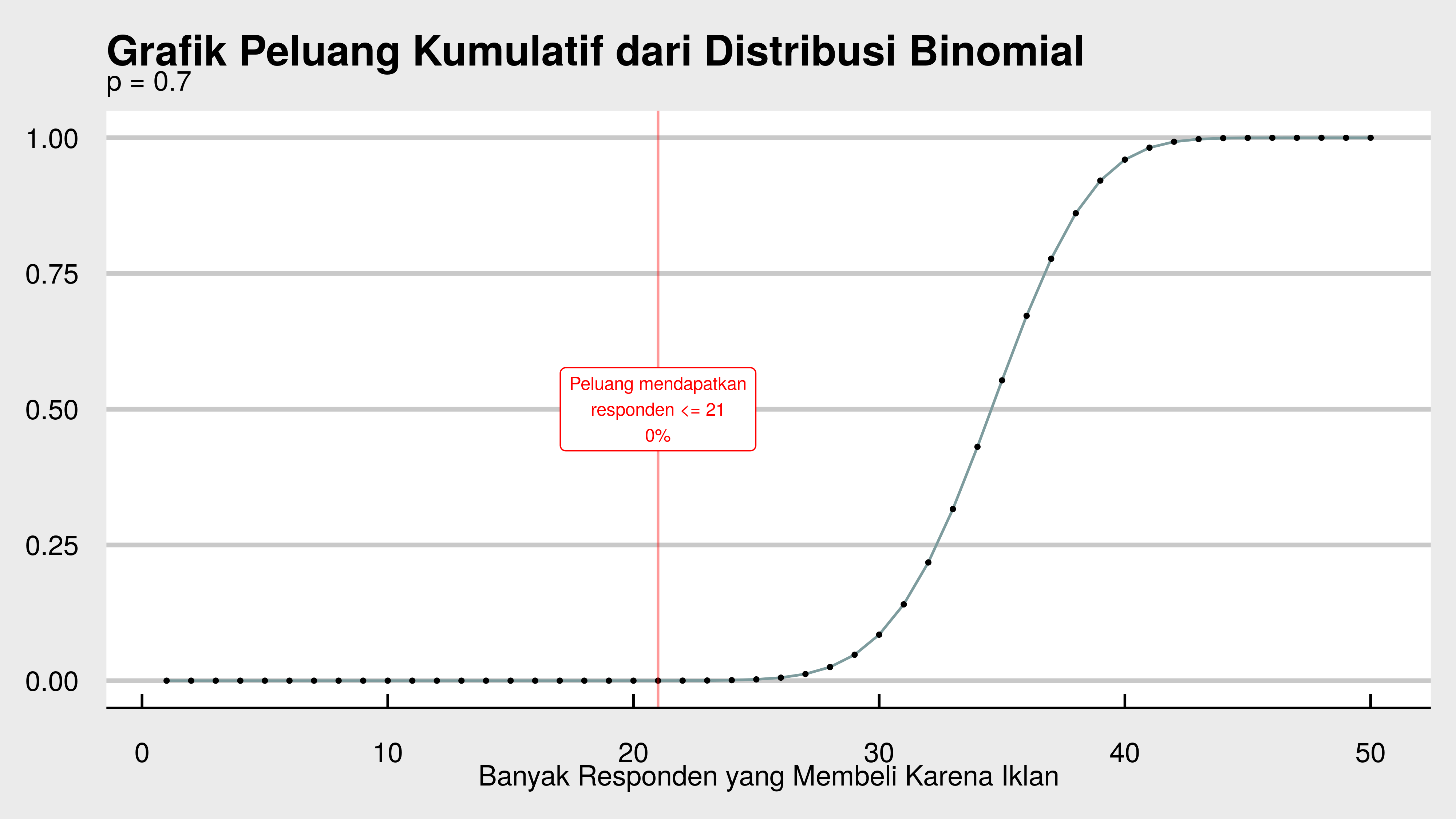
Kita bisa dapatkan bahwa peluang kita mendapatkan 21 orang responden yang membeli karena iklan adalah sebesar 0%. Sebuah angka yang sangat kecil.

Kesimpulan Sementara

Dari dua hal:

1. Besaran persentase rata-rata responden yang membeli produk karena iklan adalah sebesar 42%. Besaran persentase ini masih lebih kecil dari proporsi klaim tim digital marketing (70%).
2. Peluang mendapatkan 21 orang responden (dari total 50 orang) yang membeli karena iklan sangat kecil.

Kita bisa mengindikasikan bahwa terjadi overklaim yang dilakukan tim digital marketing.

Latas berapa angka proporsi sebenarnya?

Menentukan yang Lebih Tepat

Menggunakan formula distribusi binomial, kita bisa melakukan perhitungan sebagai berikut:

dengan = 21 dan , kita akan mencari suatu nilai yang memungkinkan.

Berikut adalah grafiknya:

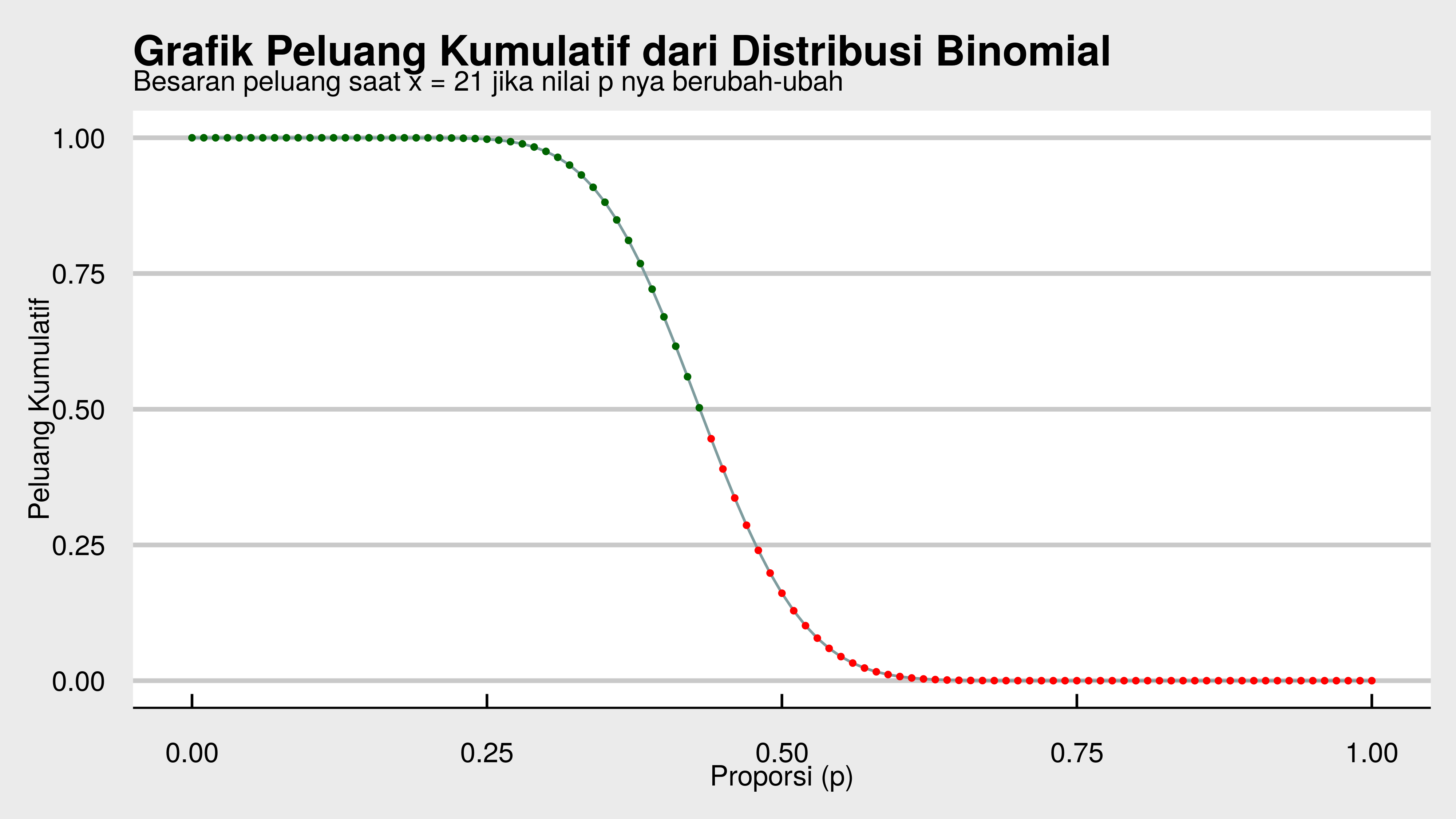
Dari grafik di atas, kita bisa hitung bahwa nilai maksimum agar kita bisa mendapatkan 21 orang responden yang membeli karena iklan digital adalah sebesar: 0.43

Kesimpulan

Dari uraian di atas, tim sales bisa memberikan koreksi terhadap klaim yang dibuat oleh tim digital marketing sehingga iklan digital yang dibuat bisa di-re-fine tuning agar lebih baik lagi.

---

if you find this article helpful, support this blog by clicking the ads.