Price Elasticity
Old but not obsolete…
Begitulah kira-kira ungkapan yang tepat dari analisa regresi linear. Walaupun usianya sudah sangat jadul tapi sampai sekarang analisa ini masih sering dipakai banyak orang karena kemudahan dalam melakukan dan menginterpretasikannya.
Analisa ini digunakan untuk memodelkan hubungan kausalitas antara
variabel independen terhadap dependen. Biasanya, regresi linear
dinotasikan dalam formula: y = a*x + b.
Di mana y dan x merupakan data numerik yang biasanya memiliki
korelasi kuat (baik positif atau negatif). Kenapa demikian? Karena salah
satu goodness of fit dari model regresi linear adalah R-Squared
yang didapatkan dengan cara mengkuadratkan angka korelasi.
Bukan cuma memodelkan x dan y saja. Untuk beberapa kasus, kita bisa
membuat optimization dari model regresi linear ini.
Contoh aplikasi regresi linear
Salah satu contoh yang paling sering saya berikan setiap kali training adalah model price elasticity.
Secara logika, semakin tinggi harga suatu barang, semakin sedikit orang
yang akan membelinya. Secara simpel kita bisa bilang bahwa harga
berkorelasi negatif dengan sales qty. Tapi untuk mengatakan ada
kausalitas antara hargadan sales qty, kita harus cek dulu model
regresinya.
Selain itu, kita ingin menghitung suatu nilai fixed (kita sebut saja
suatu price elasticity index). Dimana jika harga naik sebesar a
% maka sales qty akan turun sebesar index %_.
Sebagai catatan, ada asumsi yang kita gunakan untuk membangun model ini, yakni: tidak ada pengaruh variabel lain dalam sales qty.
Contoh yah, misalkan saya punya data jualan harian suatu barang beserta harganya di suatu minimarket sebagai berikut:
library(dplyr)
data = read.csv('/cloud/project/Materi Training/GIZ/latihan regresi.csv') %>%
mutate(X = NULL)
str(data)
## 'data.frame': 60 obs. of 3 variables:
## $ id : int 1 4 5 6 9 15 19 27 30 32 ...
## $ harga: num 18.4 17.3 21 19 15.8 17.5 17.7 15.3 17.1 21.1 ...
## $ qty : num 9.05 9.5 6.16 8.64 8.91 ...
summary(data)
## id harga qty
## Min. : 1.00 Min. :15.00 Min. : 5.632
## 1st Qu.: 40.50 1st Qu.:16.88 1st Qu.: 7.277
## Median : 74.50 Median :18.85 Median : 8.159
## Mean : 77.12 Mean :18.76 Mean : 8.013
## 3rd Qu.:118.75 3rd Qu.:20.55 3rd Qu.: 8.804
## Max. :148.00 Max. :22.00 Max. :10.626
head(data,10)
## id harga qty
## 1 1 18.4 9.0534
## 2 4 17.3 9.4958
## 3 5 21.0 6.1620
## 4 6 19.0 8.6400
## 5 9 15.8 8.9076
## 6 15 17.5 8.0800
## 7 19 17.7 8.3040
## 8 27 15.3 10.1024
## 9 30 17.1 9.2708
## 10 32 21.1 6.3516
Berapa sih nilai korelasi antara harga dan qty?
korel = cor(data$harga,data$qty)
korel
## [1] -0.8323464
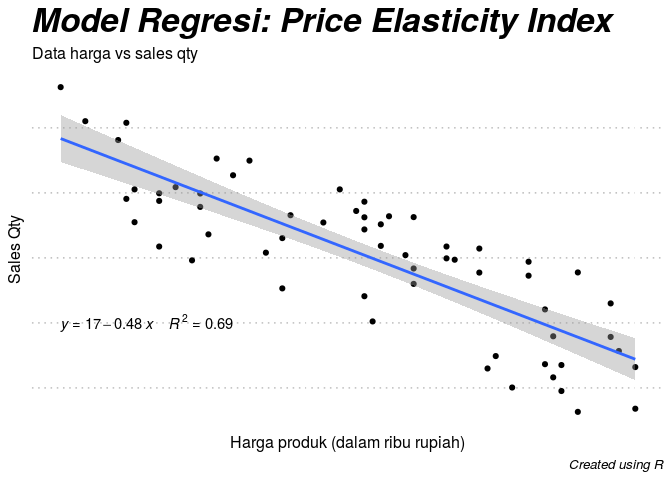
Ternyata angka korelasinya kuat negatif. Artinya, jika kita membuat model regresi linear dari kedua data ini, maka akan didapat R-Squared sebesar kuadrat nilai korelasinya. Nah, sekarang kita coba buat model regresinya yuk.
model_reg = lm(qty~harga,data = data)
summary(model_reg)
##
## Call:
## lm(formula = qty ~ harga, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.1620 -0.5572 0.1328 0.5908 0.9959
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 17.1082 0.7998 21.39 <2e-16 ***
## harga -0.4849 0.0424 -11.44 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.6545 on 58 degrees of freedom
## Multiple R-squared: 0.6928, Adjusted R-squared: 0.6875
## F-statistic: 130.8 on 1 and 58 DF, p-value: < 2.2e-16
Evaluasi model
Sekarang kita lihat goodness of fit dari model regresi di atas. Untuk mengevaluasi apakah suatu model regresi baik, kita bisa lihat dari beberapa hal seperti:
- R-squared
- P-value
- MAE ( mean absolut error )
- Lainnya
R squared
Nilainya bisa diambil dari nilai multiple R-squared pada model atau bisa juga dihitung menggunakan:
r_squared = modelr::rsquare(model_reg,data)
r_squared
## [1] 0.6928005
Mari kita cek apakah nilai R-Squared sama dengan korelasi yang dikuadratkan yah. Ini sengaja saya round biar memudahkan yah.
round(r_squared,5) == round(korel^2,5)
## [1] TRUE
R-squared bisa diartikan sebagai berapa persen variabel X meng- explain variabel Y.
P-value
Nilai P-value didapatkan dari summary(model_reg), yakni mendekati
nol (sangat kecil). Oleh karena p-value < 0.05 bisa diambil kesimpulan
bahwa model harga berpengaruh terhadap sales qty.
MAE
Mean absolut error dapat diartikan sebagai rata-rata nilai mutlak error yang dapat kita terima. Tidak ada angka pasti harus berapa, tapi semakin kecil error, berarti semakin baik model kita.
Menurut pengetahuan saya, MAE digunakan jika kita memiliki lebih dari satu model regresi yang ingin dibandingkan mana yang terbaik.
mean_absolut_error = modelr::mae(model_reg,data)
mean_absolut_error
## [1] 0.563642
Kesimpulan
Berhubung dari P-value dan R-squared menghasilkan nilai yang
baik, dapat disimpulkan bahwa harga mempengaruhi dan mengakibatkan
perubahan pada sales qty secara negatif.
Cara lain
Sebenarnya ada cara lain untuk melakukan analisa regresi linear
menggunakan R, yakni dengan memanfaatkan library ggplot2 dan
ggpubr.
library(ggplot2)
library(ggpubr)
## Loading required package: magrittr
data %>% ggplot(aes(x=harga,y=qty)) +
geom_point() +
geom_smooth(method='lm') +
theme_pubclean() +
stat_regline_equation(label.y = 7,aes(label = paste(..eq.label.., ..rr.label.., sep = "~~~~"))) +
labs(title = 'Model Regresi: Price Elasticity Index',
subtitle = 'Data harga vs sales qty',
caption = 'Created using R',
x = 'Harga produk (dalam ribu rupiah)',
y = 'Sales Qty') +
theme(axis.text = element_blank(),
axis.ticks = element_blank(),
plot.title = element_text(size=25,face='bold.italic'),
plot.caption = element_text(size=10,face='italic'))
Optimization dari model regresi
Kita telah mendapatkan model regresi linear yang baik. Kita juga sudah menghitung price elasticty index. Pertanyaan selanjutnya adalah: Apakah kita bisa menghitung harga terbaik untuk produk tersebut?
Mari kita definisikan terlebih dahulu, apa itu harga terbaik? Harga terbaik adalah harga yang membuat kita mendapatkan omset paling maksimal.
Bagaimana menghitung omset?
Omset didefinisikan sebagai: omset = harga*qty
Coba kita ingat kembali, kita telah memiliki formula regresi:
qty=m*harga + c
Jika kita substitusi persamaan qty ke persamaan omset, maka kita
akan dapatkan:
omset = harga*(m*harga + c)
omset = m*harga^2 + c*harga
Berhubung nilai m adalah negatif, maka saya bisa tuliskan persamaan
finalnya menjadi:
omset = -m*harga^2 + c*harga
Oke, mari kita ingat kuliah kalkulus I dulu. Jika kita punya persamaan kuadrat dengan konstanta depan negatif, apa artinya?
Inget Kalkulus I!
Sebagai reminder, coba yah kalau saya buat grafik dari persamaan y =
x^2 seperti di bawah ini:
x = c(-10:10)
y = x^2
contoh = data.frame(x,y)
contoh %>% ggplot(aes(x,y)) + geom_line()
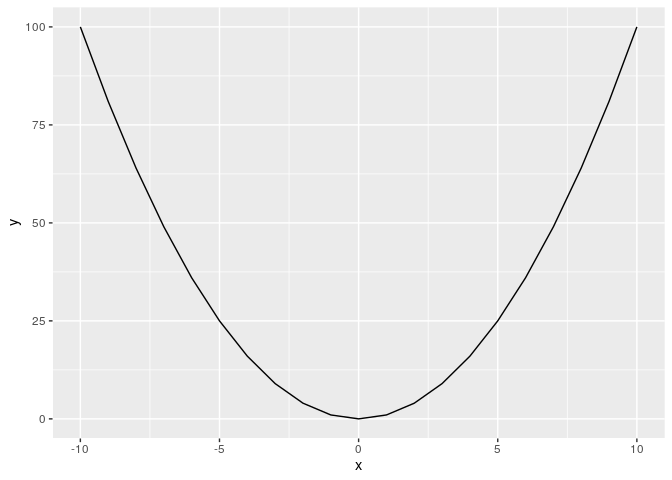
Jika kita punya persamaan kuadrat positif semacam ini, akan selalu ada
nilai x yang memberikan y minimum.
Sekarang jika saya memiliki persamaan kuadrat y = - x^2, bentuk
grafiknya sebagai berikut:
x = c(-10:10)
y = -x^2
contoh = data.frame(x,y)
contoh %>% ggplot(aes(x,y)) + geom_line()
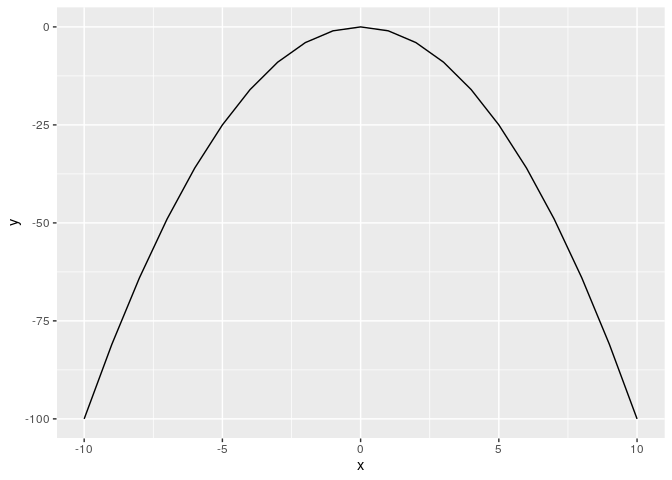
Jadi, jika kita memiliki persamaan kuadrat dengan konstanta negatif,
maka akan selalu ada nilai x yang memberikan y maksimum!
Balik lagi ke regresi kita
Nah, berhubung kita punya formula regresi berupa persamaan kuadrat, maka
dipastikan akan selalu ada harga yang memberikan omset maksimum.
Sekarang mari kita lakukan simulasi untuk mendapatkan harga paling
optimal.
harga_baru = seq(5,50,.5)
data_simulasi = data.frame(harga = harga_baru)
qty_baru = predict(model_reg,
newdata = data_simulasi)
omset = harga_baru * qty_baru
hasil = data.frame(omset,harga_baru,qty_baru)
hasil %>%
ggplot(aes(x=harga_baru,y=omset)) +
geom_line()
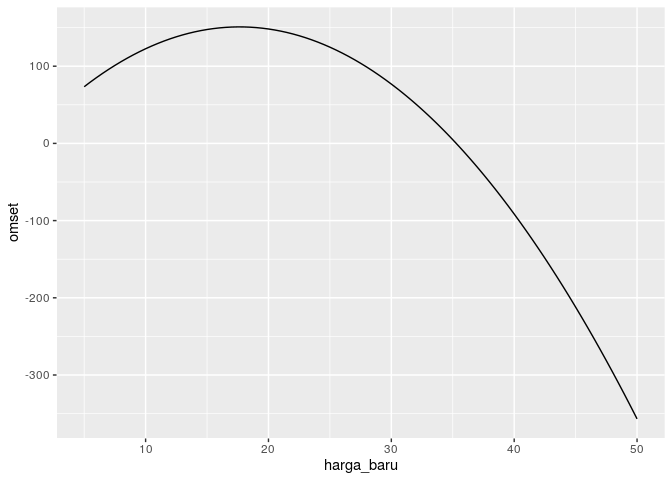
Secara grafis dapat dilihat bahwa sebenarnya ada satu titik harga_baru
yang memberikan omset paling tinggi. Yakni pada harga:
hasil %>%
filter(omset == max(omset)) %>%
select(harga_baru)
## harga_baru
## 1 17.5
So, harga optimal sudah kita dapatkan. Agak lebih rendah dibandingkan rata-rata harga yah.
Any question?