Catatan untuk Thesis: Semua Hal tentang Optimisasi part I

SEJARAH

Optimisasi

Optimisasi adalah proses mencari nilai yang optimal dari suatu masalah tertentu. Dalam matematika, optimisasi merujuk pada pencarian nilai minimal atau maksimal dari suatu fungsi real¹. Notasi matematikanya dapat ditulis sebagai berikut:

Misalkan suatu fungsi yang memetakan dari himpunan ke bilangan real.

Cari suatu nilai sedemikian sehingga:

• untuk proses minimalisasi.
• untuk proses maksimalisasi.

Di dalam kalkulus, kita mengetahui salah satu pendekatan optimisasi di fungsi satu variabel bisa didapatkan dari turunan pertama yang bernilai nol (bisa berupa nilai maksimum atau minimum dari fungsi tersebut).

Nilai disebut minimum atau maksimum di unimodal saat memenuhi:

Pierre De Fermat dan Joseph-Louis Lagrange adalah orang-orang yang pertama kali menemukan formula kalkulus untuk mencari nilai optimal. Sementara Isaac Newton dan Johann C. F.Gauss mengusulkan metode iteratif untuk mencari nilai optimal².

Salah satu bentuk optimisasi yakni linear programming dimulai oleh Leonid Kantorovich pada 1939. Metode Simplex merupakan salah satu metode penyelesaian optimisasi yang terkenal, pertama kali diperkenalkan pada 1947 oleh George Dantzig sementara di tahun yang sama Theory of Duality diperkenalkan oleh John von Neumann.

Riset Operasi

Riset operasi adalah metode antar disiplin ilmu yang digunakan untuk menganalisa masalah nyata dan membuat keputusan untuk kegiatan operasional organisasi atau perusahaan.

Riset operasi dimulai pada era Perang Dunia II. Oleh karena peperangan, diperlukan suatu cara yang efektif untuk mengalokasikan resources yang ada sehingga pihak militer Inggris dan Amerika Serikat mengumpulkan ilmuwan-ilmuwan untuk mencari pendekatan yang saintifik dalam memecahkan masalah.

Pada tahun 1940, sekelompok researchers yang dipimpin oleh PMS Blackett dari the University of Manchester melakukan studi tentang Sistem Radar Baru Anti Pesawat Terbang. Kelompok researchers ini sering dijuluki sebagai Kelompok Sirkus Blackett (Blackett’s circus). Julukan ini terjadi karena keberagaman latar belakang disiplin ilmu para researchers tersebut. Mereka terdiri dari disiplin ilmu fisiologi, matematika, astronomi, tentara, surveyor, dan fisika. Pada 1941, kelompok ini terlibat dalam penelitian radar deteksi kapal selam dan pesawat terbang. Blackett kemudian memimpin Naval Operational Research pada Angkatan Laut Kerajaan Inggris Raya. Prinsip-prinsip ilmiah yang digunakan untuk mengambil keputusan dalam suatu operasi dinamai sebagai Riset Operasi.

Saat Amerika Serikat mulai terlibat pada Perang Dunia II, prinsip riset operasi juga digunakan untuk berbagai operasi militer mereka. Kelompok riset operasi AS bertugas untuk menganalisis serangan udara dan laut tentara NAZI Jerman.

Selepas Perang Dunia II, penerapan riset operasi dinilai bisa diperluas ke dunia ekonomi, bisnis,engineering, dan sosial. Riset operasi banyak berkaitan dengan berbagai disiplin ilmu seperti matematika, statistika, computer science, dan lainnya. Tidak jarang beberapa pihak menganggap riset operasi itu overlapping dengan disiplin-disiplin ilmu tersebut.

Oleh karena tujuan utama dari aplikasi riset operasi adalah tercapainya hasil yang optimal dari semua kemungkinan perencanaan yang dibuat. Maka pemodelan matematika dan optimisasi bisa dikatakan sebagai disiplin utama dari riset operasi.

OPTIMISASI

Bahasan dalam Optimisasi

Bahasan dalam optimisasi dapat dikategorikan menjadi:

• Pemodelan masalah nyata menjadi masalah optimisasi.
• Pembahasan karakteristik dari masalah optimisasi dan keberadaan solusi dari masalah optimisasi tersebut.
• Pengembangan dan penggunaan algoritma serta analisis numerik untuk mencari solusi dari masalah tersebut.

Masalah Optimisasi

Masalah optimisasi adalah masalah matematika yang mewakili masalah nyata (real). Dari ekspresi matematika tersebut, ada beberapa hal yang perlu diketahui³, yakni:

1. Variabel adalah suatu simbol yang memiliki banyak nilai dan nilainya ingin kita ketahui. Setiap nilai yang mungkin dari suatu variabel muncul akibat suatu kondisi tertentu di sistem.
2. Parameter di suatu model matematika adalah suatu konstanta yang menggambarkan suatu karakteristik dari sistem yang sedang diteliti. Parameter bersifat fixed atau given.
3. Constraints (atau kendala) adalah kondisi atau batasan yang harus dipenuhi. Kendala-kendala ini dapat dituliskan menjadi suatu persamaan atau pertaksamaan. Suatu masalah optimisasi dapat memiliki hanya satu kendala atau banyak kendala.
4. Objective function adalah satu fungsi (pemetaan dari variabel-varibel keputusan ke suatu nilai di daerah feasible) yang nilainya akan kita minimumkan atau kita maksimumkan.

Ekspresi matematika dari model optimisasi adalah sebagai berikut:

Cari yang meminimumkan dengan kendala dan .

Dari ekspresi tersebut, kita bisa membagi-bagi masalah optimisasi tergantung dari:

1. Tipe variabel yang terlibat.
2. Jenis fungsi yang ada (baik objective function ataupun constraints).

Jenis-Jenis Masalah Optimisasi

Masalah optimisasi bisa dibagi dua menjadi dua kategori berdasarkan tipe variables yang terlibat⁴, yakni:

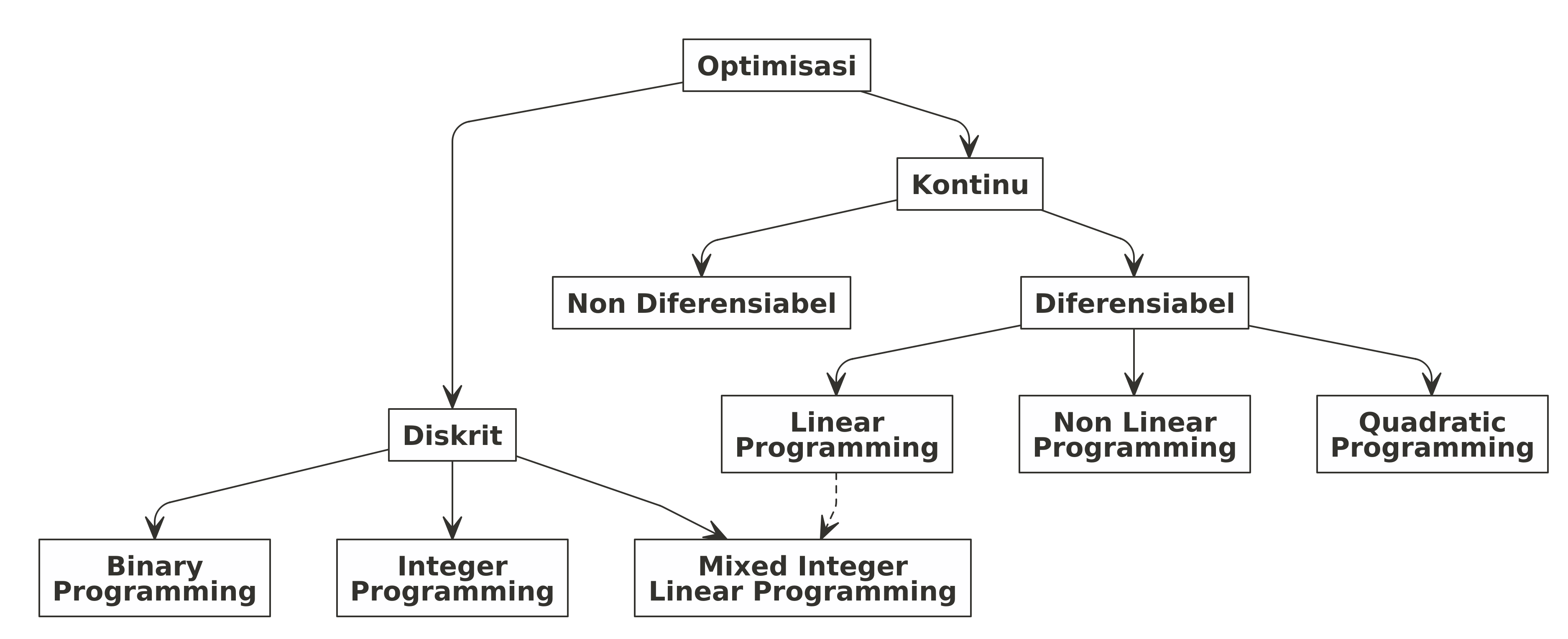
Optimisasi Berdasarkan Jenis Variabel

1. Discrete Optimization: merupakan masalah optimisasi di mana variabel yang terkait merupakan variabel diskrit, seperti binary atau integer (bilangan bulat). Namun pada masalah optimisasi berbentuk mixed integer linear programming, dimungkinkan suatu masalah optimisasi memiliki berbagai jeni variabel yang terlibat (integer dan kontinu sekaligus).
2. Continuous Optimization: merupakan masalah optimisasi di mana variabel yang terkait merupakan variabel kontinu (bilangan real). Pada masalah optimisasi jenis ini, fungsi-fungsi yang terlibat bisa diferensiabel atau tidak. Konsekuensinya adalah pada metode penyelesaiannya.

Selain itu, kita juga bisa membagi masalah optimisasi berdasarkan kepastian nilai variable dan parameter yang dihadapi sebagai berikut:

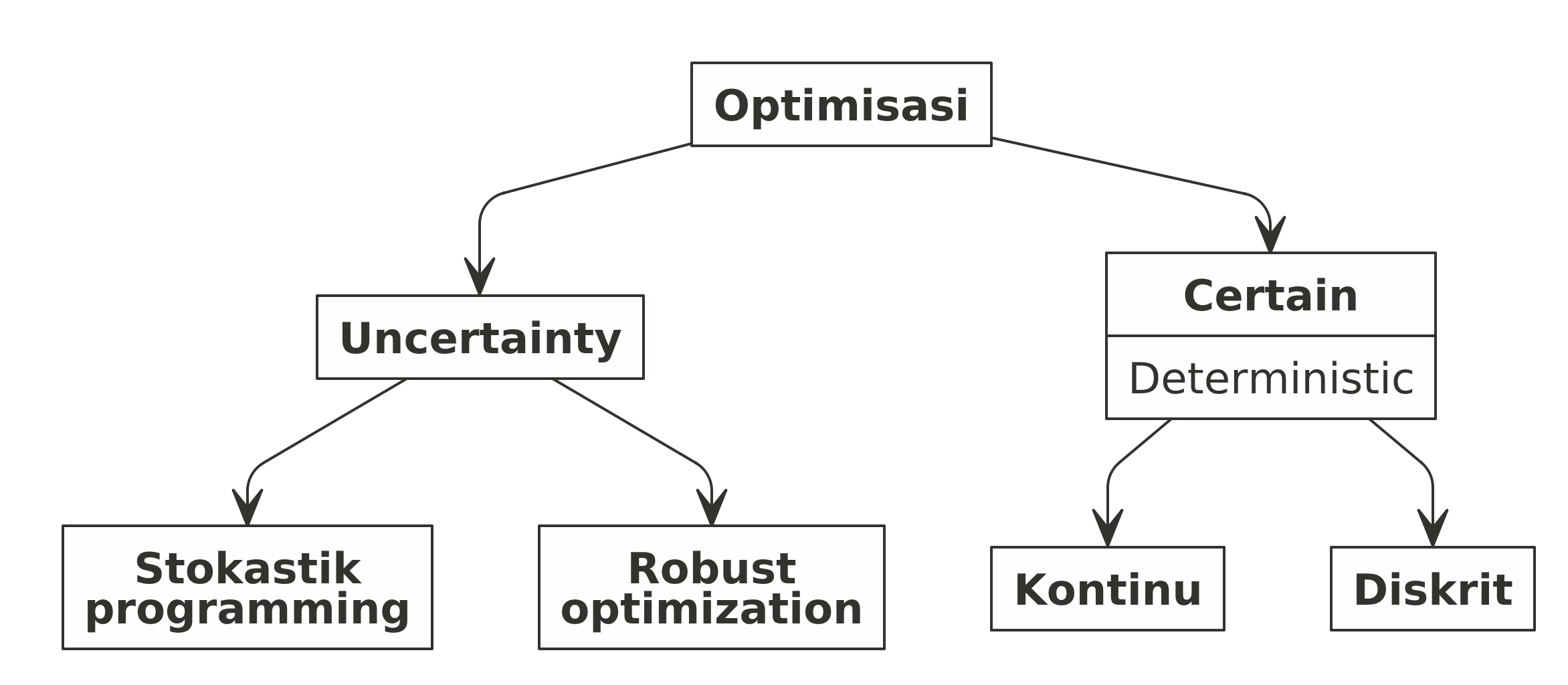
Optimisasi Berdasarkan Kepastian Nilai

1. Optimization under uncertainty⁵; Pada beberapa kasus di dunia real, data dari masalah tidak dapat diketahui secara akurat karena berbagai alasan. Hal ini mungkin terjadi akibat:
   • Kesalahan dalam pengukuran, atau
   • Data melibatkan sesuatu di masa depan yang belum terjadi atau tidak pasti. Contoh: demand produk, harga barang, dan sebagainya.
2. Deterministic optimization;
   • Model deterministik adalah model matematika di mana nilai dari semua parameter dan variabel yang terkandung di dalam model merupakan satu nilai pasti.
   • Pendekatan deterministik memanfaatkan sifat analitik masalah untuk menghasilkan barisan titik yang konvergen ke solusi optimal.
   • Semua algoritma perhitungan mengikuti pendekatan matematis yang ketat.

1. https://id.wikipedia.org/wiki/Optimisasi ↩

2. https://empowerops.com/en/blogs/2018/12/6/brief-history-of-optimization ↩

3. Pengantar Riset Operasi dan Optimisasi, KampusX: PO101 ↩

4. Optimization problem. https://en.wikipedia.org/wiki/Optimization_problem ↩

5. https://neos-guide.org/content/optimization-under-uncertainty ↩