Apakah Penjualan Naik Karena Promosi atau Kebetulan Saja?

Sepanjang tahun ini, sebagai seorang market researcher, pertanyaan yang paling sering ditanyakan kepada saya (dan paling sulit) dijawab adalah:

“Apakah kenaikan sales bulan lalu murni karena campaign marketing kita, atau karena faktor lain (seasonal, tren, atau random event tertentu)?”

Untuk menjawab pertanyaan ini, biasanya kita bisa menggunakan beberapa alternatif seperti:

• Menghitung korelasi dengan adanya gap waktu.
• Menggunakan Granger-Causality untuk menemukan efek antar data time series.
• Membandingkan nilai rata-rata before-after iklan atau promosi lainnya.

---

Pada tulisan ini, saya akan memberikan satu alternatif cara menjawab yang lain.

Semalam saya tak sengaja menemukan satu repository milik Google di Github bernama Causal Impact. Causal Impact merupakan library di R yang bertujuan untuk menyelesaikan permasalahan bisnis di atas dengan pendekatan Bayesian.

Apa itu Causal Impact?

Causal Impact Analysis adalah pendekatan statistik yang memungkinkan kita untuk mengukur efektivitas sebenarnya dari suatu intervensi, seperti marketing campaign, strategi harga, atau peluncuran produk baru. Metode ini dirancang untuk memisahkan dampak nyata dari faktor luar noise yang dapat mengaburkan hasil, seperti tren pasar, efek musiman, dan peristiwa makroekonomi. Intinya, analisis ini mengevaluasi dampak dengan membandingkan hasil aktual yang diobservasi dengan “counterfactual”, yaitu sebuah simulasi atau prediksi tentang apa yang seharusnya terjadi jika intervensi tersebut tidak pernah dilakukan.

Cara kerja analisis ini secara umum melibatkan penggunaan model deret waktu struktural Bayesian (Bayesian structural time-series models) untuk mengonstruksi prediksi counterfactual tersebut. Prosesnya dimulai dengan menetapkan periode waktu sebelum intervensi (sebagai baseline) dan periode setelah intervensi untuk dianalisis. Model kemudian menggunakan data historis dan variabel kontrol (seperti data pasar yang tidak terkena intervensi) untuk membangun kelompok kontrol sintetis yang mencerminkan karakteristik kelompok intervensi.

Dampak kausal ditentukan dengan menghitung selisih antara data aktual yang diamati dan prediksi counterfactual selama periode setelah intervensi, yang kemudian dapat divisualisasikan untuk melihat perkembangan efeknya secara bertahap maupun kumulatif.

Penggunaan metode ini sangat bergantung pada beberapa asumsi kunci agar kesimpulan yang dihasilkan tetap valid. Asumsi yang paling utama adalah bahwa variabel kontrol yang digunakan tidak ikut terpengaruh oleh intervensi tersebut; jika variabel kontrol juga terdampak, maka model akan menghasilkan estimasi dampak yang salah. Selain itu, model mengasumsikan bahwa hubungan antara variabel kontrol dan variabel target tetap stabil sejak periode sebelum hingga periode sesudah intervensi dilakukan. Terakhir, efektivitas analisis ini sangat mensyaratkan adanya data berkualitas tinggi, akurat, dan lengkap, karena data yang hilang atau salah dapat menyebabkan bias pada hasil akhir dan melemahkan kekitalan model.

Sebagai analogi untuk membantu pemahaman, bayangkan kita ingin mengetahui dampak nyata dari sebuah pupuk baru terhadap pertumbuhan satu tanaman tertentu. Causal Impact bekerja seperti membandingkan tinggi tanaman yang diberi pupuk tersebut dengan “saudara kembarnya” yang dibesarkan dalam kondisi cahaya, tanah, dan air yang identik namun tanpa diberi pupuk; perbedaan tinggi di antara keduanya adalah dampak nyata yang disebabkan oleh pupuk tersebut.

Inti dari Causal Impact adalah menemukan Counterfactual. Bayangkan sebuah dunia paralel (multiverse) di mana:

• Dunia Nyata: Kita menjalankan diskon besar-besaran di suatu periode waktu sehingga terlihat sales value naik.
• Dunia Counterfactual: Di waktu yang sama, kita tidak menjalankan diskon.

Selisih antara sales value Dunia Nyata dan sales value Dunia Counterfactual itulah yang disebut Causal Impact.

Oleh karena saya tidak punya mesin transportasi ke dunia paralel, saya harus memprediksinya menggunakan data statistik. Kita akan membuat Synthetic Control (garis basis prediksi) berdasarkan data historis dan variabel kontrol.

Perbedaan dengan A/B Testing

Berdasarkan penjelasan di atas, lantas apa perbedaannya dengan A/B Testing?

Sebagai analogi, A/B testing seperti melakukan uji laboratorium yang terkontrol ketat di mana kita membagi dua tanaman identik sejak awal, sedangkan Causal Impact seperti melihat sebuah tanaman di hutan yang tumbuh pesat setelah diberi pupuk, lalu menggunakan data cuaca dan pertumbuhan tanaman di sekitarnya untuk mensimulasikan seberapa tinggi tanaman itu seharusnya tumbuh jika pupuk tersebut tidak pernah diberikan.

Business Question

Dalam bisnis, seringkali kita memiliki pertanyaan:

Apa hubungan antara budget promosi yang digelontorkan dengan sales yang diraih?

Jika kita sengaja menaikkan budget promosi sebagai bagian dari intervensi untuk meningkatkan sales, validitas analisis Causal Impact dapat terganggu jika budget tersebut digunakan sebagai variabel kontrol (kovariat). Hal ini dikarenakan salah satu asumsi paling krusial dalam metode ini adalah bahwa variabel kontrol (kovariat) tidak boleh terpengaruh oleh intervensi itu sendiri

Oleh karena itu perlu dipilih variabel kontrol lainnya yang tidak terpengaruh oleh promosi yang dilakukan.

Oke, saya akan coba gunakan satu contoh sebagai berikut:

Case Study

Misalkan saya adalah memiliki dua toko retail di salah satu kota tertentu. Saya memiliki data sales selama 100 hari untuk kedua toko tersebut. Pada hari ke-71 hingga 100, saya melakukan intervensi berupa flash sale pada toko A. Sedangkan pada toko B tidak ada flash sale sama sekali. Saya hendak mengetahui berapa uplift murni yang disebabkan oleh flash sale tersebut.

Saya memiliki data tanggal, sales toko A, dan sales toko B.

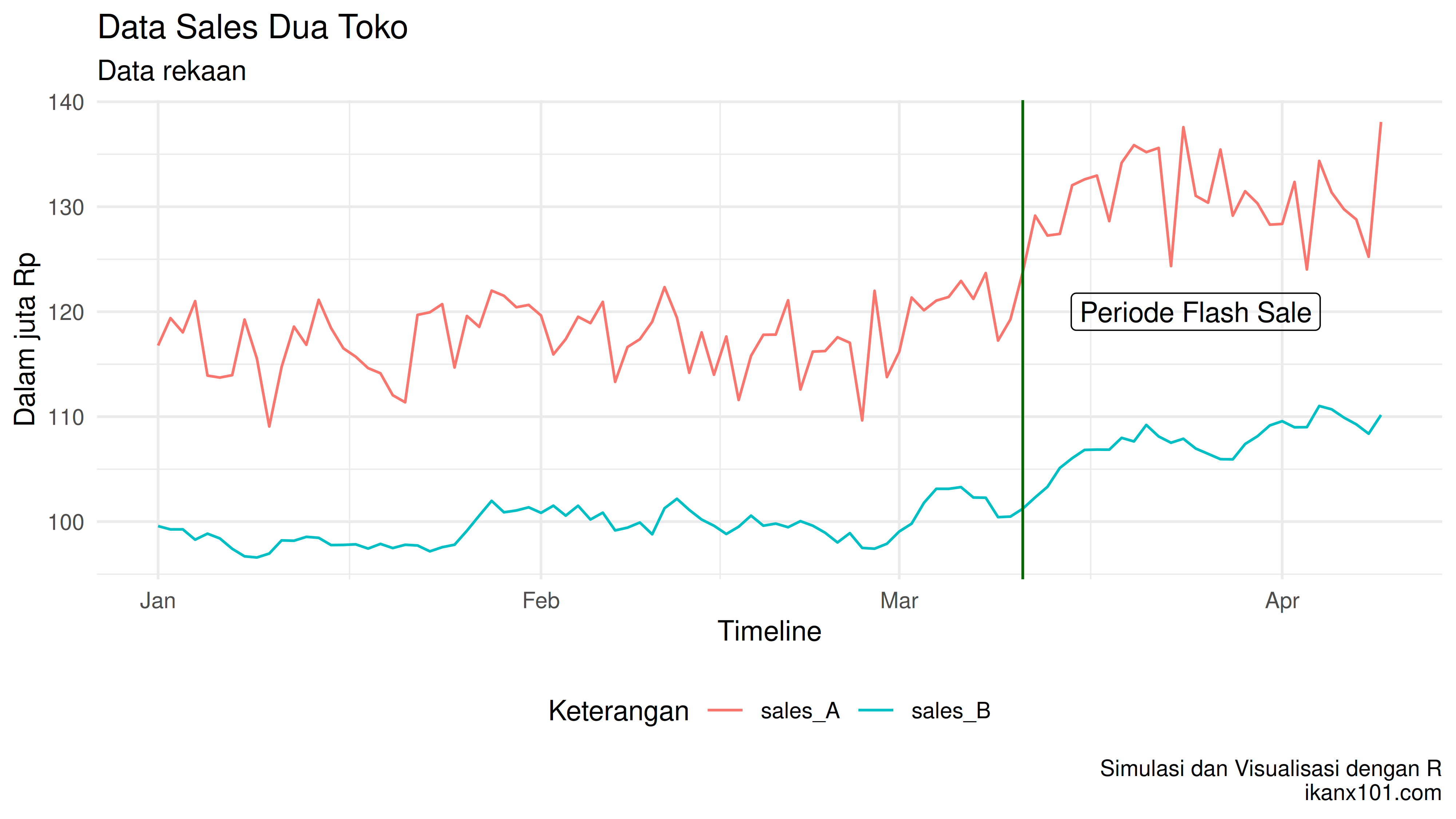
Jika kita lihat, sales pada toko B juga mengalami peningkatan pada periode flash sale di toko A padahal tidak dilakukan promosi sama sekali. Analisa ini bisa membantu untuk melihat apakan flash sale benar-benar ngefek atau tidak.

Causal Impact bekerja dengan memodelkan hubungan antara sales A dan sales B selama periode sebelum flash sale (intervensi) dilakukan. Model ini menggunakan sales B sebagai prediktor untuk membangun counterfactual, yaitu estimasi penjualan yang seharusnya terjadi jika intervensi tersebut tidak ada.

Sebagai perumpamaan, variabel kontrol (budget) bertindak seperti “kompas” yang memberitahu model ke mana arah penjualan seharusnya pergi; jika penjualan tiba-tiba melonjak melampaui petunjuk kompas tersebut tepat saat promosi dimulai, itulah yang kita sebut sebagai dampak kausal.

Di sini saya akan mendefinisikan kapan periode Pre-Intervention (sebelum promo) dan Post-Intervention (saat promo). Model akan belajar pola hubungan antara sales A dan sales B pada masa Pre-Intervention, lalu memproyeksikan apa yang seharusnya terjadi di masa Post-Intervention jika promo tidak ada.

# Tentukan periode sebelum dan sesudah intervensi
pre.period <- as.Date(c("2024-01-01", "2024-03-10")) # Hari 1-70
post.period <- as.Date(c("2024-03-11", "2024-04-09")) # Hari 71-100 (Flash Sale)

# Jalankan model
impact <- CausalImpact(data, pre.period, post.period)

# Mari kita lihat hasilnya
plot(impact)

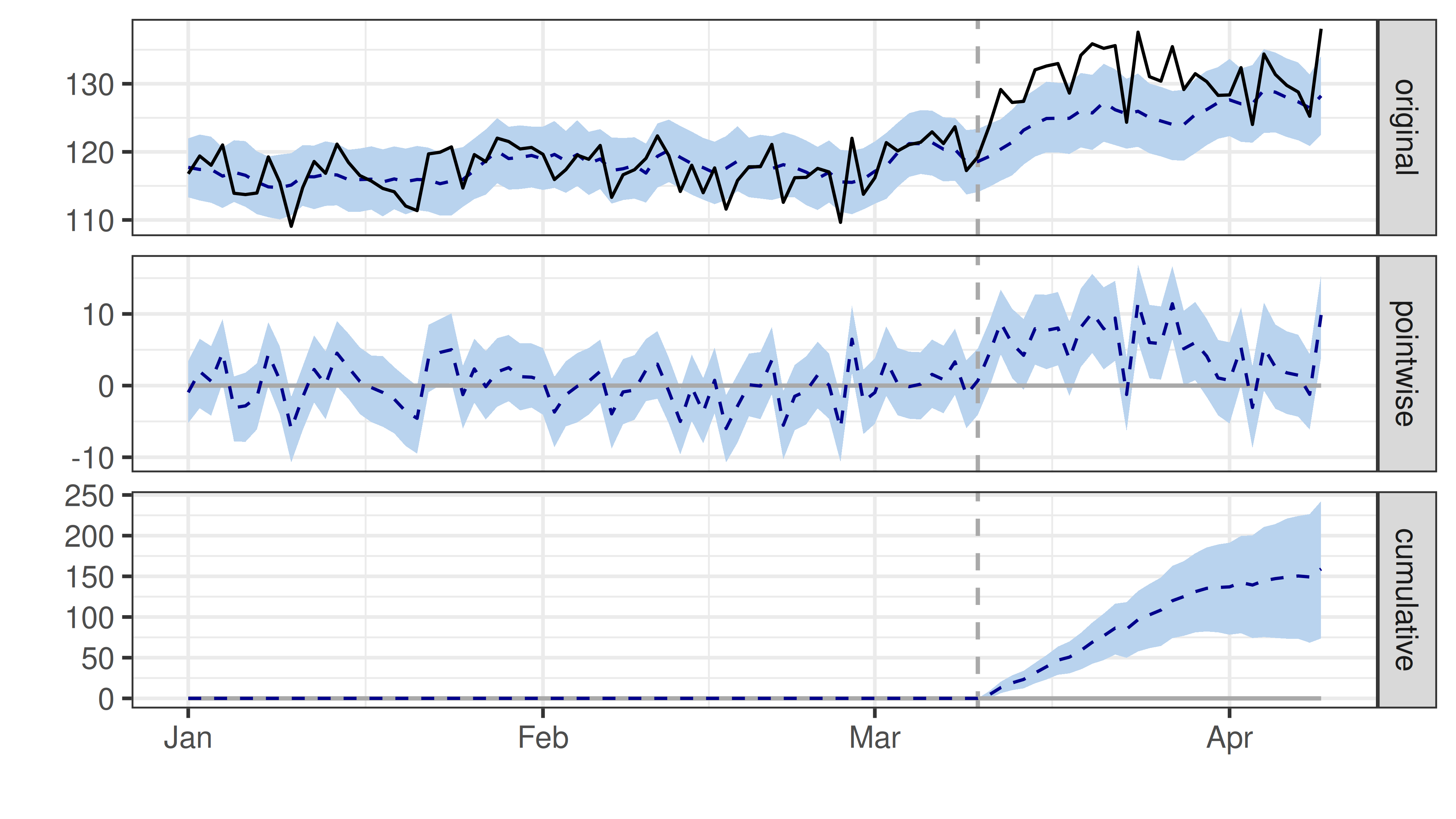
Dari grafik impact di atas, kita mendapatkan tiga panel grafik yang sangat informatif sebagai berikut:

1. Original (panel teratas):
   • Garis Hitam Solid: Data sales asli (yang terjadi).
   • Garis Biru Putus-putus: Prediksi sales jika tidak ada Flash Sale (counterfactual).
   • Insights:
     • Pada periode flash sale kita bisa lihat bahwa hampir semua garis hitam berada di atas garis biru.
     • Walaupun beberapa kali kedua garis tersebut merapat.
2. Pointwise (panel tengah):
   • Grafik ini menunjukkan selisih antara Garis Hitam dan Garis Biru per hari dari grafik panel teratas.
   • Grafik ini menunjukkan seberapa besar uplift harian yang kita dapatkan.
3. Cumulative (panel terbawah):
   • Penjumlahan kumulatif dari uplift harian.
   • Grafik ini menunjukkan secara kumulatif harian berapa sales ekstra yang di-generate akibat flash sale.

Saya akan mengeluarkan summary dari model sebagai berikut:

Posterior inference {CausalImpact}

                         Average        Cumulative   
Actual                   131            3925         
Prediction (s.d.)        126 (1.4)      3766 (43.1)  
95% CI                   [123, 128]     [3683, 3851] 
                                                     
Absolute effect (s.d.)   5.3 (1.4)      159.1 (43.1) 
95% CI                   [2.5, 8.1]     [73.6, 242.4]
                                                     
Relative effect (s.d.)   4.2% (1.2%)    4.2% (1.2%)  
95% CI                   [1.9%, 6.6%]   [1.9%, 6.6%] 

Posterior tail-area probability p:   0.001
Posterior probability of an effect:  99.9%

For more details, type: summary(impact, "report")

Fitur terbaik dari library(CausalImpact) adalah saya bisa meminta library ini memberikan penjelasan dari summary di atas sebagai berikut:

Analysis report {CausalImpact}


During the post-intervention period, the response variable had an average value of approx. 130.84. 
By contrast, in the absence of an intervention, we would have expected an average response of 125.54. 
The 95% interval of this counterfactual prediction is [122.76, 128.38]. 
Subtracting this prediction from the observed response yields an estimate of the causal effect the intervention had on the response variable. 
This effect is 5.30 with a 95% interval of [2.45, 8.08]. For a discussion of the significance of this effect, see below.

Summing up the individual data points during the post-intervention period (which can only sometimes be meaningfully interpreted), the response variable had an overall value of 3.93K. 
By contrast, had the intervention not taken place, we would have expected a sum of 3.77K. 
The 95% interval of this prediction is [3.68K, 3.85K].

The above results are given in terms of absolute numbers. 
In relative terms, the response variable showed an increase of +4%. 
The 95% interval of this percentage is [+2%, +7%].

This means that the positive effect observed during the intervention period is statistically significant and unlikely to be due to random fluctuations. 
It should be noted, however, that the question of whether this increase also bears substantive significance can only be answered by comparing the absolute effect (5.30) to the original goal of the underlying intervention.

The probability of obtaining this effect by chance is very small (Bayesian one-sided tail-area probability p = 0.001). 
This means the effect is statistically significant. 
It can be considered causal if the model assumptions are satisfied. 
For more details, including the model assumptions behind the method, see https://google.github.io/CausalImpact/. 

Kita bisa melihat seberapa besar dampak dari flash sale yang dilakukan dan bisa memutuskan apakah flash sale ini cukup worth untuk dilakukan atau tidak.

Catatan Penting

Analisa ini membutuhkan covariate (variabel kontrol) yang bagus. Tanpa variabel kontrol yang bagus, model ini hanya akan menjadi time-series forecasting biasa.

---

if you find this article helpful, support this blog by clicking the ads.