Belajar Regresi dengan Deep Learning menggunakan TensorFlow di Google Colab
Tulisan ini saya ambil langsung dari materi training yang saya bawakan di kantor dalam rangkaian Workshop Deep Learning with TensorFlow using Google Colab.
Pendahuluan: TensorFlow di Google Colab
TensorFlow adalah salah satu open source tools buatan Google untuk
membuat model deep learning. Basisnya TensorFlow adalah Python.
Keunggulannya:
- Tidak perlu di-install (bisa menjalankan via cloud).
- Modelnya bisa di-transfer dan dipakai di computing environment lainnya. Model bisa disimpan dalam suatu object dan dimasukkan ke dalam mesin Google Cloud.
- Tersedia dalam bahasa R atau Python.
Kelemahan:
- Instalasi di Windows mungkin akan lebih rumit.
- Saat ada version update, beberapa skrip mungkin akan berubah.
Untuk bisa menggunakan TensorFlow, kita harus meng-install
library(keras) pada Google Colab. Selain itu, jika diperlukan kita
juga meng-install library(caret) yang berguna untuk melakukan
beberapa pre-processing ala machine learning di R.
Dalam beberapa kasus, kita perlu melakukan “sedikit” pre-processing sebelum kita melatih modelnya.
Pada kasus regresi ini, saya tidak akan menggunakan library(caret).
Secara garis besar, alur kerjanya meliputi:
- Input,
- Berupa matriks untuk predictors dan matriks untuk target.
- Process,
- Berapa banyak layer, nodes, dan activation function.
- Berapa banyak epoch, learning rate, dan validation split.
- Output.
- Berupa tensor object bertipe vector yang berisi:
- Probabilitas untuk klasifikasi, dan
- Value untuk regresi dan forecast time series.
- Berupa tensor object bertipe vector yang berisi:
Mari kita mulai:
Regresi Menggunakan Deep Learning
Apakah kalian ingat saat learning forum terdahulu, saya pernah
menginformasikan bahwa deep learning adalah artificial neural
network di mana setiap nodes-nya berisi operasi regresi linear.
Sehingga semakin besar dan banyak neural network yang terlibat, maka
ANN menjadi sebuah mega mesin regresi linear.
Kali ini kita akan membuat model regresi linear menggunakan deep learning.
Soal
Dari data yang diberikan, buatlah model yang bisa menyerupai
sebagai berikut:
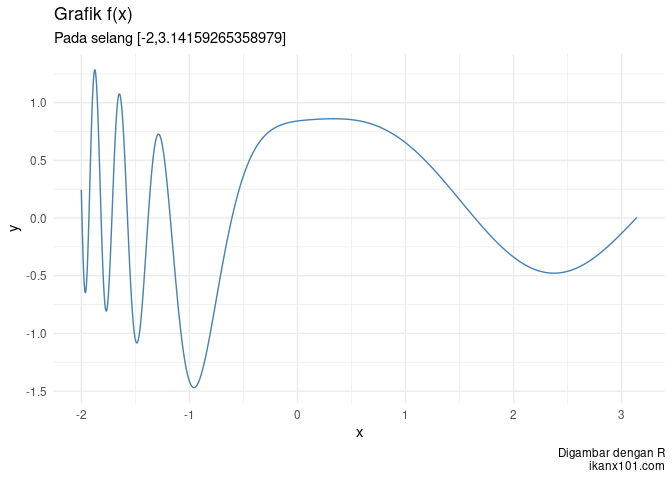
Namun sebelum kita membuat model deep learning, apakah kita bisa
mendapatkan
menggunakan regresi linear atau polinomial biasa?
Kita coba terlebih dahulu ya.
# dimulai dari nol
rm(list=ls())
# kita panggil libraries
library(dplyr)
library(ggplot2)
library(caret)
library(keras)
library(tensorflow)
# ambil data
link = "https://raw.githubusercontent.com/ikanx101/Live-Session-Nutrifood-R/master/LEFO%20Market%20Research/LEFO%20MR%202023/Keras/regresi/soal_regresi.csv"
df = read.csv(link)
# membuat model regresi linear
lin_model = lm(y ~ x,data = df)
pred_y1 = predict(lin_model,df)
# membuat model regresi polinom
# derajat 26
poli_model = lm(y ~ polym(x,degree = 26),data = df)
pred_y2 = predict(poli_model,df)
# menggabungkan
df_hasil = df |> mutate(y_linear = pred_y1,y_polinom = pred_y2)
# membuat plot y = f(x)
df_hasil |>
ggplot() +
# plot fungsi soal
geom_line(aes(x = x,y = y),group = 1,color = "blue") +
# plot pendekatan dengan regresi linear
geom_line(aes(x = x,y = y_linear),group = 1,color = "red") +
# plot regresi polinom dengan derajat 26
geom_line(aes(x = x,y = y_polinom),group = 1,color = "darkred")

Terlihat bahwa model dengan polinom derajat 26 bisa mendekati
dengan
lebih baik. Perhatikan nilai mean absolute error berikut ini:
## mae_linear mae_poli
## 1 0.5382325 0.1099523
Apakah mungkin kita melakukan modifikasi data tertentu sehingga hasil regresi polinomnya menjadi lebih akurat?
Jawabannya tentu saja. Saya akan buat data dummy sebagai berikut:
# kita modifikasi terlebih dahulu
df_modif =
df |>
mutate(x1 = x^2,
x2 = x^3,
x3 = x^4,
x4 = sin(x),
x5 = cos(x),
x6 = exp(x))
# kita intip datanya
head(df_modif,5)
## x y x1 x2 x3 x4 x5 x6
## 1 -2.0000 0.2460495 4.0000 -8.000000 16.0000 -0.9092974 -0.4161468 0.1353353
## 2 -1.9999 0.2419973 3.9996 -7.998800 15.9968 -0.9093390 -0.4160559 0.1353488
## 3 -1.9998 0.2379480 3.9992 -7.997600 15.9936 -0.9093806 -0.4159650 0.1353624
## 4 -1.9997 0.2339016 3.9988 -7.996401 15.9904 -0.9094222 -0.4158740 0.1353759
## 5 -1.9996 0.2298581 3.9984 -7.995201 15.9872 -0.9094638 -0.4157831 0.1353894
Sekarang kita akan buat model polinom derajat 15 sebagai berikut:
# membuat model regresi polinom
# derajat 15
poli_model2 = lm(y ~ poly(x,15) + poly(x1,15) + poly(x2,15) + poly(x3,15) +
poly(x4,15) + poly(x5,15) + poly(x6,15),data = df_modif)
pred_modif = predict(poli_model2,df_modif)
# menggabungkan hasil modif ke df_hasil
df_hasil = df_hasil |> mutate(y_modif = pred_modif)
# membuat plot y = f(x)
df_hasil |>
ggplot() +
# plot fungsi awal dari soal warna biru
geom_line(aes(x = x,y = y),group = 1,color = "blue",linewidth = 5,alpha = .5) +
# plot hasil regresi polinom dengan data modifikasi
geom_line(aes(x = x,y = y_modif),group = 1,color = "black")

Secara visual kita bisa melihat bahwa garis hitam bisa mendekati garis biru dengan baik. Sekarang kita akan hitung kembali nilai mean absolute error dari hasil model modifikasi tersebut.
# menghitung mean absolute error
df_hasil |>
mutate(error_linear = abs(y - y_linear),
error_poli = abs(y - y_polinom),
error_modif = abs(y - y_modif)) |>
summarise(mae_linear = mean(error_linear),
mae_poli = mean(error_poli),
mae_modif = mean(error_modif))
## mae_linear mae_poli mae_modif
## 1 0.5382325 0.1099523 0.0136809
Mean absolute error dari model dengan data modifikasi memiliki nilai terkecil (akurasi terbaik).
Sekarang bagaimana menyelesaikan soal ini dengan deep learning?
Membuat Model Deep Learning
Proses-prosesnya adalah sebagai berikut:
- Pisahkan predictors dan target.
- Ubah keduanya menjadi tipe matriks.
- Buat modelnya (layers, nodes, activation function, optimizers, epochs, etc.)
- Train dan validation.
# deep learning
# langkah 1 dan 2
predictors = df |> pull(x) |> as.matrix()
target = df |> pull(y) |> as.matrix()
# tahap 3
# buat model
model = keras_model_sequential() %>%
layer_dense(units = 86, activation="relu", input_shape = ncol(predictors)) %>%
layer_dense(units = 21, activation = "relu") %>%
layer_dense(units = 12, activation = "relu") %>%
layer_dense(units = 7, activation = "relu") %>%
layer_dense(units = 1, activation = "linear")
# optimizer
model %>% compile(
loss = "mse",
optimizer = "adam",
metrics = list("mean_absolute_error")
)
# summary model
model %>% summary()
## Model: "sequential"
## ________________________________________________________________________________
## Layer (type) Output Shape Param #
## ================================================================================
## dense_4 (Dense) (None, 86) 172
## dense_3 (Dense) (None, 21) 1827
## dense_2 (Dense) (None, 12) 264
## dense_1 (Dense) (None, 7) 91
## dense (Dense) (None, 1) 8
## ================================================================================
## Total params: 2,362
## Trainable params: 2,362
## Non-trainable params: 0
## ________________________________________________________________________________
# proses train dengan 100 epoch
model %>% keras::fit(predictors, target, epochs = 100,verbose = 0)
# tahap 4
# proses validasi dengan menghitung nilai mean absolute error
scores = model %>% evaluate(predictors, target, verbose = 0)
print(scores)
## loss mean_absolute_error
## 0.001888338 0.021335045
Kita dapatkan bahwa model dengan deep learning bisa memiliki mean obsolute error yang relatif kecil (hampir sama dengan hasil model dengan data yang dimodifikasi).
Kita buat plot-nya sebagai berikut:
# kita buat prediksinya
y_deep = model %>% predict(predictors)
# menggabungkan hasil deep learning ke df_hasil
df_hasil = df_hasil |> mutate(y_deep = y_deep)
# membuat plot y = f(x)
df_hasil |>
ggplot() +
# plot awal fungsi dari soal
geom_line(aes(x = x,y = y),group = 1,color = "blue",linewidth = 5,alpha = .5) +
# plot hasil prediksi dari model deep learning
geom_line(aes(x = x,y = y_deep),group = 1,color = "black")
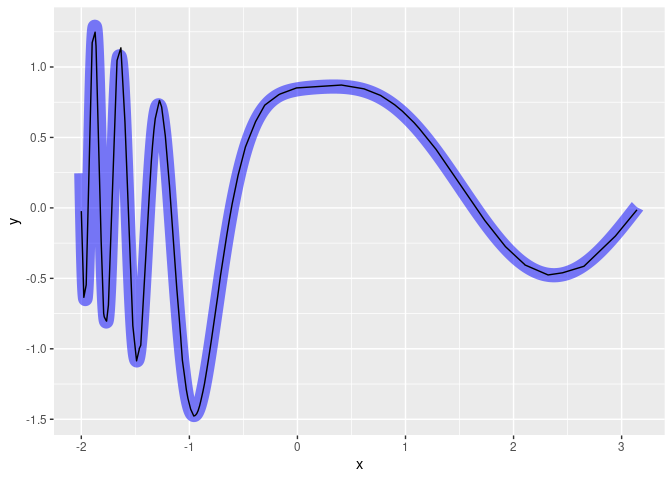
Pertanyaannya lagi:
Bagaimana jika kita memasukkan data dari
df_modif?
Apakah akurasi model yang didapatkan bisa lebih bagus lagi?
# deep learning
# langkah 1 dan 2
predictors = df_modif |> select(-y) |> as.matrix()
target = df_modif |> pull(y) |> as.matrix()
# tahap 3
# buat model
model_modif = keras_model_sequential() %>%
layer_dense(units = 86, activation="relu", input_shape = ncol(predictors)) %>%
layer_dense(units = 21, activation = "relu") %>%
layer_dense(units = 12, activation = "relu") %>%
layer_dense(units = 7, activation = "relu") %>%
layer_dense(units = 1, activation = "linear")
# optimizer
model_modif %>% compile(
loss = "mse",
optimizer = "adam",
metrics = list("mean_absolute_error")
)
# summary model
model_modif %>% summary()
## Model: "sequential_1"
## ________________________________________________________________________________
## Layer (type) Output Shape Param #
## ================================================================================
## dense_9 (Dense) (None, 86) 688
## dense_8 (Dense) (None, 21) 1827
## dense_7 (Dense) (None, 12) 264
## dense_6 (Dense) (None, 7) 91
## dense_5 (Dense) (None, 1) 8
## ================================================================================
## Total params: 2,878
## Trainable params: 2,878
## Non-trainable params: 0
## ________________________________________________________________________________
# proses train
model_modif %>% keras::fit(predictors, target, epochs = 100,verbose = 0)
# tahap 4
# proses validasi
scores = model_modif %>% evaluate(predictors, target, verbose = 0)
print(scores)
## loss mean_absolute_error
## 0.0001994848 0.0065981704
Ternyata kita dapatkan hasil yang lebih baik.
Kita buat plot-nya kembali:
# kita buat prediksinya
y_deep_modif = model_modif %>% predict(predictors)
# menggabungkan hasil deep learning ke df_hasil
df_hasil = df_hasil |> mutate(y_deep_2 = y_deep_modif)
# membuat plot y = f(x)
df_hasil |>
ggplot() +
# plot awal fungsi dari soal
geom_line(aes(x = x,y = y),group = 1,color = "blue",linewidth = 5,alpha = .5) +
# plot hasil prediksi dari model deep learning dengan data modifikasi
geom_line(aes(x = x,y = y_deep_2),group = 1,color = "black")
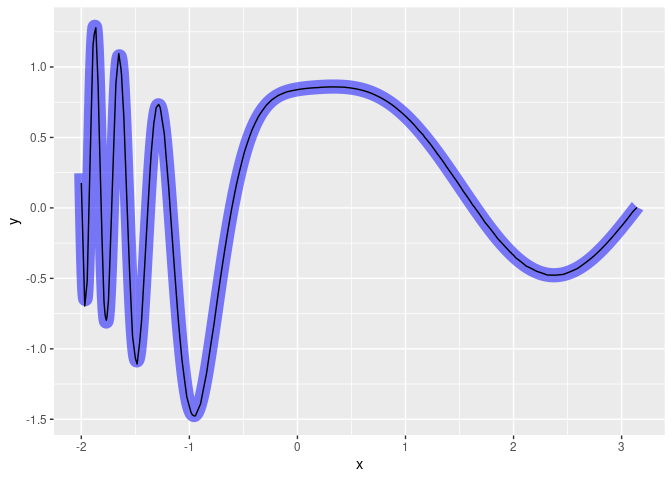
Apakah regresi dengan deep learning tidak memiliki kelemahan?
Walaupun regresi dengan deep learning sangat baik menghampiri nilai aslinya, ada satu hal yang perlu kita perhatikan, yakni:
Model yang terbentuk hanya bisa digunakan pada domain (atau defined range) si predictors saja.
Ilustrasi:
Berikut adalah nilai dari
dari soal
di atas untuk
.

Kita akan hampiri nilai
menggunakan model deep learning yang telah kita buat pada bagian
sebelumnya:

if you find this article helpful, support this blog by clicking the ads.
Video dari tulisan ini saya post di Youtube saya berikut ini:
