Bunch of Ideas, a little bit of Maths.

I am mathematician doing market research and data science

24 minute read

Pendahuluan

Sebagaimana yang kita ketahui bersama, WHO beberapa hari yang lalu telah mengumumkan bahwa kasus COVID-19 menjadi pandemi. Penyebarannya dinilai semakin masif dan tidak terkontrol di beberapa negara. Politisi, artis, bahkan olahragawan dunia sudah terserang penyakit tersebut.

Angka Statistik COVID-19

Konon katanya, secara perhitungan statistika, COVID-19 tidak begitu berbahaya dibandingkan dengan penyakit lainnya. Jika saya mengambil sumber dari situs www.worldometers.info, justru persentase kesembuhannya lebih tinggi.

Namun hal ini jangan membuat kita lengah dan tidak waspada.

Kenapa? Karena nilai R0 dari COVID-19 berada di rentang yang relatif tidak jauh dari penyakit mumps yang pernah mampir di beberapa tempat tahun lalu.

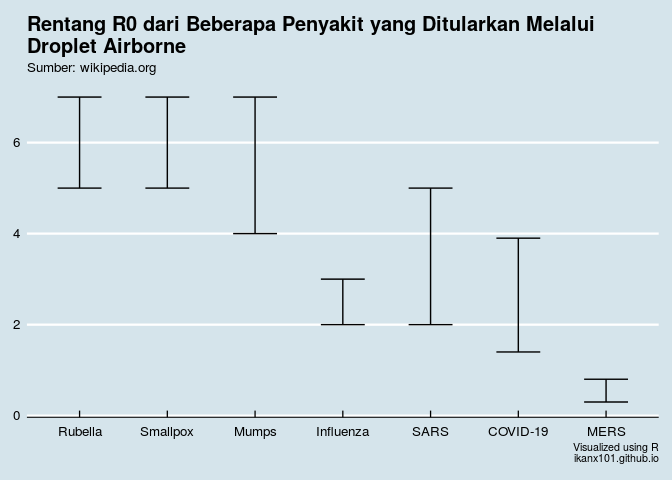
Apa itu R0? Penjelasannya bisa dilihat di sini. Angka ini nantinya yang akan membantu saya dalam membuat model penyebaran penyakit.

Pertanyaan yang Sering Muncul

Di beberapa WhatsApp Group yang saya ikuti, sering saya menemukan pertanyaan:

  1. Sampai kapan virus ini akan menyebar?
  2. Apa sih yang harus dilakukan untuk meminimalisir penyebaran virus ini?

Untuk menjawab pertanyaan-pertanyaan tersebut, lebih mudah bagi saya untuk membuat modelnya sehingga saya bisa sekalian memperlihatkan apa yang mungkin bisa terjadi.

Model ini tidak saya tujukan untuk membuat prediksi atau forecast. Saya hanya ingin menjelaskan kondisi saat ini dan apa yang bisa kita lakukan bersama.

Model Penyebaran Penyakit

Sewaktu kuliah di Matematika dulu, saya pernah mempelajari dan membuat model matematika sederhana untuk memformulasikan penyebaran penyakit Kusta di Jawa Barat. Kerja sama antara ITB dan Dinkes Provinsi Jawa Barat.

Berdasarkan ilmu yang saya ketahui, saya mencoba membuat model matematika sederhana yang bisa menggambarkan situasi penyebaran virus ini.

Apa perbedaan model matematika dan model statistika?

Perbedaan mendasar adalah model matematika bisa dibangun tanpa menggunakan data. Data hanya digunakan untuk menaksir parameter dalam model. Walaupun demikian, model ini tetap robust karena bisa divalidasi menggunakan data juga.

Sedangkan model statistika dibangun berdasarkan keseluruhan atau sebagian dari data yang ada.

Membuat model matematika

Dalam membuat model penyebaran penyakit COVID-19 ini, masih ada beberapa limitasi dan asumsi yang saya gunakan. Oleh karena itu, saya tekankan kembali bahwa model ini adalah sebagai indikasi saja.

Compartment Model

Model penyebaran penyakit biasa disebut compartmental model. Ada dua jenis model, yakni:

  1. SIR model.
  2. SIS model.

Apa bedanya?

SIR model

Merupakan singkatan dari Susceptible, Infectious, dan Recovered.

  • Susceptible, yakni orang-orang yang sehat dan rentan terhadap penyakit.
  • Infectious, yakni orang-orang yang sudah tertular penyakit dan bisa menularkan ke orang yang sehat.
  • Recovered, yakni orang-orang yang sudah sembuh dan menjadi imun terhadap penyakit tersebut.

Digunakan untuk memodelkan perubahan jumlah orang per satuan waktu di masing-masing kelompok di atas.

Asumsi dasar pada model ini adalah orang yang sembuh tidak mungkin tertular kembali.

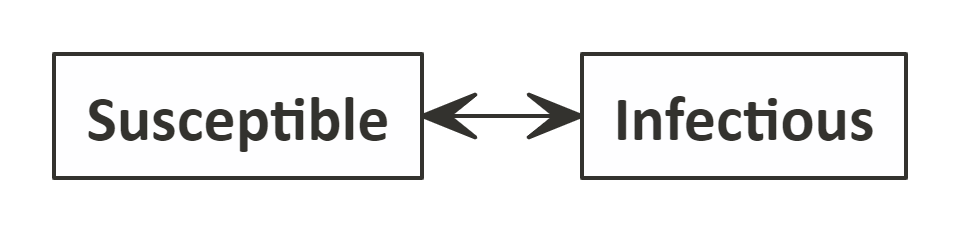
SIS Model

Merupakan singkatan dari Susceptible, Infectious, dan Susceptible.

  • Susceptible, yakni orang-orang yang sehat (atau orang yang sudah sembuh) dan rentan terhadap penyakit.
  • Infectious, yakni orang-orang yang sudah tertular penyakit dan bisa menularkan ke orang yang sehat.

Digunakan untuk memodelkan perubahan jumlah orang per satuan waktu di masing-masing kelompok di atas.

Asumsi dasar pada model ini adalah orang yang sembuh mungkin tertular kembali.

Lalu Pilih Model yang Mana?

Dari kasus COVID-19, kita tahu bahwa pasien yang sembuh ternyata bisa tertular lagi.

Oleh karena itu saya akan menggunakan SIS Model yang akan dimodifikasi.

Modifikasi di bagian apa?

Kita ketahui bersama-sama bahwa ada peluang pasien yang terkena penyakit COVID-19 meninggal akibat komplikasi. Karena pada SIS Model, secara default tidak ada kelompok pasien yang meninggal akibat penyakit tersebut.

Membuat SIS Model

Persamaan Differensial

Perlu saya sampaikan bahwa model matematika yang akan dibangun ini berlandaskan persamaan diferensial. Jika kita ingat pelajaran saat SMA dulu, kita pernah belajar mengenai turunan. Nah itu adalah persamaan diferensial.

Kenapa menggunakan persamaan diferensial?

Persamaan diferensial biasa digunakan untuk menyelesaikan permasalahan yang menyangkut perubahan dalam kondisi atau satuan tertentu.

Masih ingat pelajaran Fisika Klasik saat SMA dulu? Itu adalah salah satu contoh persamaan diferensial.

  • Misalkan s(t) adalah jarak pada waktu tertentu (t).
  • Kecepatan bisa kita definisikan sebagai perubahan jarak dalam satuan waktu, yakni: v(t) = \frac{d s(t)}{dt}.
  • Sedangkan percepatan bisa kita definisikan sebagai perubahan kecepatan dalam satuan waktu, yakni: a(t) = \frac{d v(t)}{dt} = \frac{d s(t)}{dt^2}

Kembali ke SIS model yah. Sekarang saya akan membangun tiga persamaan diferensial yang merepresentasikan kelompok pada SIS model saya. Satuan waktu yang saya gunakan adalah hari.

Berikut adalah tiga kelompok yang akan dibangun persamaannya?

S(t), I(t), D(t)

Susceptible S(t)

Pada awalnya, hampir semua orang termasuk ke dalam kelompok ini, yakni sehat namun rentan. Tidak ada bukti yang cukup bahwa ada orang yang secara alami imun terhadap virus ini. Sehingga kita bisa buat hipotesa sementara bahwa semua orang yang sehat berpeluang untuk menjadi sakit.

Saya bisa tuliskan saat awal waktu, (t = 0) banyaknya S(0) sama dengan banyaknya orang di populasi minus seorang yang sakit (saya tulis sebagai N - 1).

Perubahan banyaknya orang yang sehat diasumsikan HANYA berasal dari dua hal:

Orang Sehat yang Menjadi Sakit

Orang sehat menjadi sakit akibat berinteraksi dengan orang yang sakit (sehingga tertular). Interaksi ini dituliskan dalam bahasa matematika:

\beta*S(t)*I(t)

Dimana \beta adalah laju orang yang sehat menjadi tertular karena berinteraksi dengan orang yang sakit.

Pada model sederhana ini, diasumsikan orang sehta dan sakit saling berinteraksi. Belum ada karantina atau social distancing antara kedua kelompok tersebut.

Nah, dalam model ini menentukan nilai \beta adalah hal yang krusial.

Bagaimana caranya?

Akan saya bahas di section di bawah yah.

Orang Sakit yang Telah Pulih

Orang yang pulih dari kondisi sakitnya dan berpeluang yang kemudian untuk sakit kembali. Kondisi ini bisa dituliskan dalam bahasa matematika:

\gamma * I(t)

Dimana \gamma adalah recovery rate: laju kesembuhan pasien yang sakit menjadi sehat dengan sendirinya (tanpa pengobatan) dalam satuan waktu. Sebagaimana yang kita ketahui bersama, COVID-19 diklaim sebagai self limiting disease yang bisa sembuh dengan sendirinya.

\gamma = 1 / days

Dimana days adalah lama hari yang diperlukan hingga seseorang yang sakit sembuh sendiri.

Sehingga kita bisa tuliskan persamaan final untuk Susceptible adalah sebagai berikut:

dS(t) = -\beta*S(t)*I(t) + \gamma * I(t)

Jadi diasumsikan perubahan angka orang sehat ini tidak dipengaruhi oleh angka kelahiran, angka kematian normal, dan angka migrasi.

Infectious I(t)

Infectious adalah kumpulan orang-orang yang sakit. Saya bisa tuliskan saat awal waktu, (t = 0) banyaknya I(0) adalah 1 orang.

Perubahan banyaknya orang yang sakit diasumsikan HANYA berasal dari tiga hal:

Orang Sehat yang Menjadi Sakit

Penjelasan section ini sama dengan section sebelumnya.

Orang Sakit yang Telah Pulih

Penjelasan section ini sama dengan section sebelumnya.

Orang Sakit yang Meninggal

Kita ketahui bersama bahwa COVID-19 bisa menyebabkan komplikasi yang berujung pada kematian. Walau dinilai angkanya relatif masih kecil, tapi perlu saya masukkan ke dalam model.

Kelompok ini saya tuliskan dalam persamaan berikut ini:

D(t) = \zeta * I(t)
Dimana \zeta adalah angka death rate seorang pasien meninggal dalam satuan hari.

Sehingga kita bisa tuliskan persamaan final untuk Infectious adalah sebagai berikut:

dI(t) = \beta*S(t)*I(t) - \gamma * I(t) - \zeta * I(t)

Death D(t)

Merupakan kelompok pasien COVID-19 yang meninggal akibat komplikasi yang dialaminya. Penjelasannya sama dengan section sebelumnya.

Menaksir Parameter Model

Berdasarkan uraian di atas, maka persamaan diferensial untuk model saya adalah sebagai berikut:

dS(t) = -\beta*S(t)*I(t) + \gamma * I(t)

dI(t) = \beta*S(t)*I(t) - \gamma * I(t) - \zeta * I(t)

dD(t) = \zeta * I(t)

Untuk menaksir parameter, saya akan menggunakan data dan informasi publik yang tersedia. Jika ada data yang berada dalam range, maka saya akan gunakan expected value dari data range tersebut.

Expected value yang saya ambil adalah nilai tengah dari range tersebut.

Menaksir 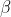\beta

Menurut literatur dari Stanford University, R0 dihitung dari:

R0 = \tau*c*d

  • \tau adalah transmissibility yakni probability of infection given contact between a susceptible and infected individual.
  • c adalah average rate of contact between susceptible and infected individuals.
  • d adalah duration of infectiousness.

Sayangnya saya tidak memiliki data yang cukup untuk menghitung \tau, c, dan d. Oleh karena itu, saya memerlukan cara alternatif untuk menghitung \beta.

Dari literatur lain dari UC Santa Barbara R0 juga bisa dihitung dari hubungan antara:

R0 = \frac{\beta}{\gamma}

Expected value dari R0 adalah: 2.65.

Maka, nilai \beta akan bisa ditaksir saat kita mengetahui \gamma.

Menaksir 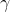\gamma

Pada section sebelumnya kita tahu bahwa:

\gamma = 1 / days

Menurut informasi yang saya dan beberapa teman kumpulkan, beberapa pasien COVID-19 bisa self healing dalam waktu sekitar 14 hari.

Maka bisa saya taksir bahwa \gamma = 0.071.

Maka nilai \beta menjadi 0.189.

Menaksir 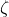\zeta

Dari data yang ada di worldometers.info, saya akan menaksir death rate dalam satuan hari dengan cara:

\zeta = \frac{totaldeaths}{allcases} * \frac{1}{totaldays}
Yakni, berapa persen pasien meninggal dari keseluruhan kasus dalam rentang waktu mulai dari pertama kali kasus ini muncul hingga saat ini.

Pertama kali COVID-19 terdeteksi adalah pada 31 Desember.

zeta = (5821 / 156433) * (1 / (1+31+29+15))

Maka bisa saya taksir bahwa \zeta = 4.910^{-4}.

Menyelesaikan Model Persamaan Diferensial

Berdasarkan penaksiran parameter tersebut, maka kita dapatkan persamaannya menjadi:

dS(t) = -0.189*S(t)*I(t) + 0.071 * I(t)

dI(t) = 0.189*S(t)*I(t) - 0.071 * I(t) - 4.910^{-4} * I(t)

dD(t) = 4.910^{-4} * I(t)

Untuk menyelesaikan persamaan ini, saya menggunakan R dengan packages deSolve.

library(deSolve)
SIS.model <- function(N,I,t, b, g, z){
  require(deSolve)
  init <- c(S=(N-I)/N,I=I/N,D=0)
  parameters <- c(bet=b,gamm=g,zet=z)
  time <- seq(0,t,by=t/(2*length(1:t)))
  eqn <- function(time,state,parameters){
    with(as.list(c(state,parameters)),{
      dS <- -bet*(S)*I + gamm*I
      dI <- bet*S*I - gamm*I - zet*I 
      dD <- zet*I
      return(list(c(dS,dI,dD)))})}
  out<-ode(y=init,times=time,eqn,parms=parameters)
  out.df<-as.data.frame(out)
  
  subtit <- bquote(list(beta==.(parameters[1]),
                        ~gamma==.(parameters[2]),
                        ~zeta==.(parameters[3])))
  
  ggplot(out.df,aes(x=time))+
    ggtitle(bquote(atop(bold(.(title)),atop(bold(.(subtit))))))+
    geom_line(aes(y=S,colour="Susceptible"),size=1.5)+
    geom_line(aes(y=I,colour="Infected"))+
    geom_line(aes(y=D,colour="Death"))+
    labs(x = 'Waktu dalam hari',
         y = 'Proporsi',
         title = 'Simple SIS Model',
         caption = 'Solved and Visualized\nusing R\nikanx101.github.io',
         subtitle = subtit) +
    theme(legend.position='bottom')+
    theme(legend.title=element_text(size=12,face="bold"),
          legend.background = element_rect(fill='#FFFFFF',
                                           size=0.5,linetype="solid"),
          legend.text=element_text(size=10),
          legend.key=element_rect(colour="#FFFFFF",
                                  fill='#C2C2C2',
                                  size=0.25,
                                  linetype="solid"))+
    scale_colour_manual("Compartments",
                        breaks=c("Susceptible","Infected",'Death'),
                        values=c("blue","red",'black'))
}

Misalkan dalam satu lingkungan berisi 1000 orang dengan 999 orang sehat dan 1 orang yang sakit, maka kondisinya dalam 200 hari menjadi sebagai berikut:

SIS.model(1000,1,200,beta,gamm,zeta)

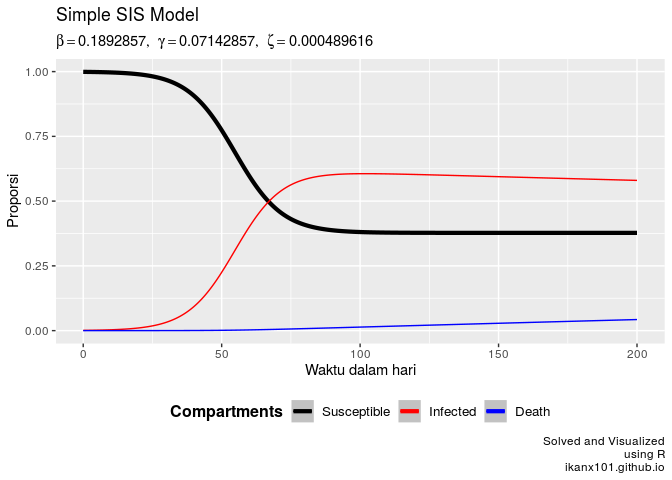
Dimulai pada hari ke-60an, maka persentase orang sakit akan mulai melebihi persentase orang yang sehat.

Saya ingatkan kembali yah, kondisi di atas terjadi sesuai dengan asumsi saat saya membuat modelnya.

Menjawab pertanyaan pertama pada section sebelumnya:

Infectious akan mencapai peak saat porporsi orang sehat tinggal 37.74%.

Atau dari kurva di atas terlihat di medio hari ke-75 hingga hari ke-100. Setelah itu laju infectious akan terus menurun.

Simulasi untuk Berbagai Nilai Parameter \beta

Kita tahu bahwa nilai R0 berada pada range tertentu. Oleh karena itu, saya akan coba simulasi untuk beberapa nilai R0 tersebut.

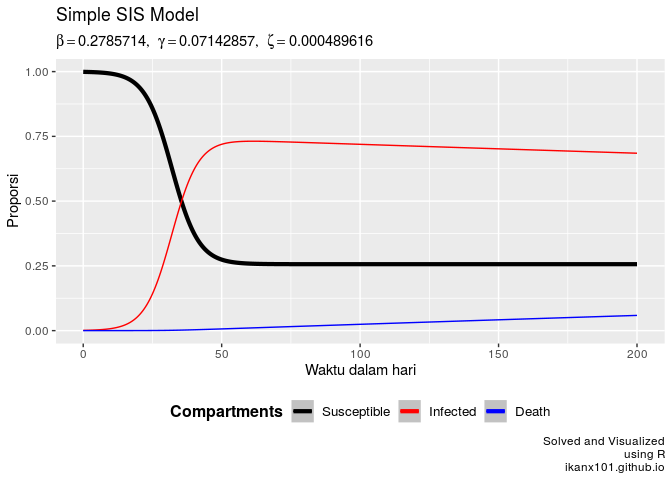
Simulasi pada saat R0 max

beta_max = 3.9 * gamm
SIS.model(1000,1,200,beta_max,gamm,zeta)

Simulasi pada saat R0 min

beta_min = 1.4 * gamm
SIS.model(1000,1,1000,beta_min,gamm,zeta)

Kondisi Real Saat Ini

Kalau kita melihat grafik-grafik di atas, saya merasa hal ini masih lebih aman dibandingkan kejadian real saat ini di Indonesia atau Jabodetabek.

Kenaikan real yang ada jauh lebih tinggi.

Tau gak kenapa?

Karena banyaknya I(0) pada ilustrasi di atas hanya 1.

Sedangkan dalam kasus real, I(0) adalah sejumlah pasien yang terkena COVID-19 dari imported cases. Tiba-tiba saja beberapa orang yang baru pulang dari luar negeri terinfeksi. Jadi bukan dari 1 orang lalu menyebar, tapi dimulai dari sekian orang lalu menyebar.

Kita akan lakukan simulasi untuk beberapa nilai I(0) dengan nilai R0 tetap (expected value) sebagai berikut yah:

Saat I(0) = 10

SIS.model(1000,10,200,beta,gamm,zeta)

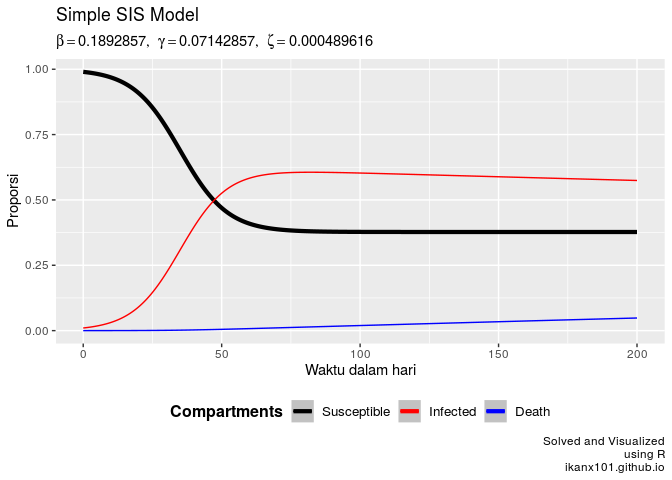
Saat I(0) = 15

SIS.model(1000,15,200,beta,gamm,zeta)

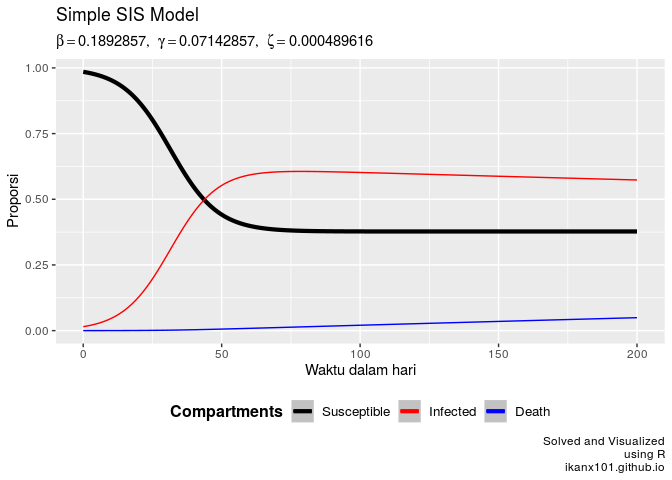
Saat I(0) = 20

SIS.model(1000,20,200,beta,gamm,zeta)

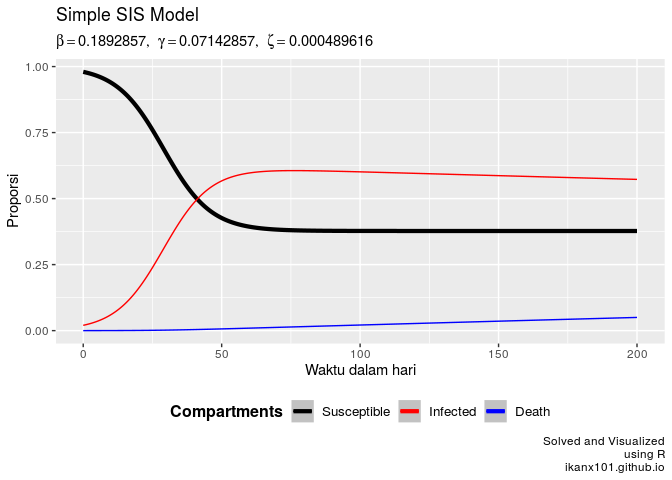
Saat I(0) = 25

SIS.model(1000,25,200,beta,gamm,zeta)

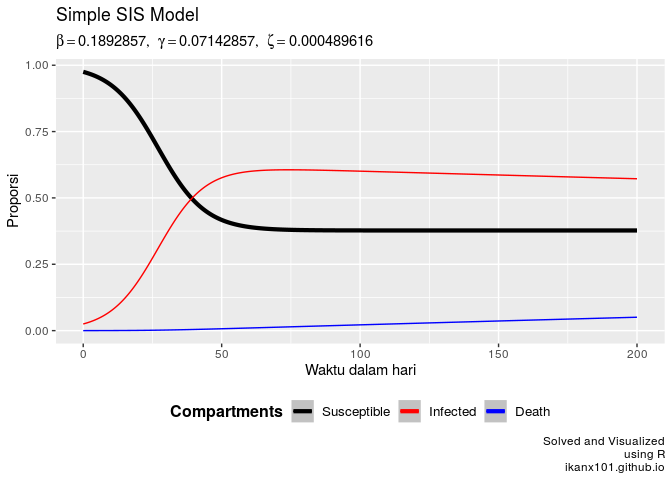
Saat I(0) = 40

SIS.model(1000,40,200,beta,gamm,zeta)

Kesimpulan

Bagaimana menjawab pertanyaan kedua pada section sebelumnya?

Menurunkan 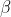\beta

Berdasarkan model sederhana ini, hal paling mudah yang bisa dilakukan adalah dengan menurunkan angka \beta. Dari persamaan di atas kita tahu bahwa \beta berbanding lurus dengan \tau, c, d.

\beta \sim \tau*c*d

Parameter d tidak mungkin kita turunkan karena itu adalah karakteristik dari virus itu sendiri. Oleh karena itu, hal yang paling mungkin kita lakukan adalah menurunkan \tau dan c.

Konkritnya:

  1. Menurunkan transmissibility salah satunya dengan cara menggunakan masker bagi yang sakit sesuai anjuran dari WHO ATAU disiplin dalam melakukan social distancing agar droplet virus tidak mengenai orang yang sehat.
  2. Menurunkan average rate of contact between susceptible and infected individuals dengan cara karantina dan self isolation bagi orang yang sakit ATAU membatasi interaksi dengan orang banyak.

Meninggikan 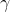\gamma

Apakah mungkin \gamma dinaikkan? Sementara waktu ini kita hanya bisa berharap riset-riset yang dilakukan di berbagai negara bisa membuat obat yang efektif dan vaksin untuk COVID-19 ini.

Mengetahui angka pasti I(0)

COVID-19 ini dimulai dari imported cases, yakni orang yang masuk ke Indonesia dalam keadaan sakit yang kemudian menularkannya ke masyarakat. Maka I(0) bisa dilihat sebagai berapa banyak orang sakit dari luar negeri yang masuk ke Indonesia sejak wabah di Wuhan merebak.

Semakin besar I(0) akan semakin mempercepat penyebaran infeksi kepada masyarakat. Oleh karena itu, penting sekali bagi pemerintah untuk mendeteksi secara dini berapa banyak I(0) lalu segera melakukan karantina terhadap mereka.

Masalahnya adalah keran orang masuk dari luar negeri masih dibuka sampai kemudian ditutup beberapa hari yang lalu.

Ingat kasus almarhum pegawai Telkom Kab. Bekasi yang ternyata positif Corona? Beliau positif sebelum diumumkannya kasus 01 dan 02.

What’s next?

Saya sadar betul bahwa model ini dibangun atas keterbatasan yang dimiliki dari data publik. Oleh karena itu, untuk iterasi berikutnya semoga saja data publik yang ada sudah cukup untuk membangun model yang lebih baik lagi.

Proses validasi akan dilakukan untuk menaksir parameter model dengan lebih akurat lagi.

Stay safe.

You May Also Enjoy

Geocoding di R Menggunakan tidygeocoder

7 minute read

Di blog ini saya sudah menuliskan berbagai macam metode dan teknik pengambilan data longlat dari alamat (vice versa). Istilah kerennya itu geocoding.