Menyelesaikan Persamaan Diophantine Menggunakan Simulasi Monte Carlo

Beberapa waktu lalu, di suatu mata kuliah, saya diberi tugas untuk menyelesaikan persamaan diophantine berikut ini:

• Cari solusi dari:
  1. .
  2. .
  3. .
  4. .

Menggunakan suatu algoritma optimisasi spiral. Suatu saat nanti, saya akan membahas banyak terkait algoritma optimisasi spiral ini yah. Karena algoritma ini tergolong algoritma meta heuristic yang baru dikembangkan, saya butuh satu metode lain untuk mengecek apakah jawaban saya sudah benar atau belum.

Top of mind saya langsung menuju simulasi Monte Carlo. Simulasi sangat powerful untuk menyelesaikan berbagai macam masalah matematis (tentunya dengan advantages dan disadvantages tersendiri).

---

Persamaan Diophantine

Definisi:

Persamaan diophantine adalah persamaan suku banyak yang masing-masing sukunya berupa bilangan bulat (integer).

---

Alur Simulasi Monte Carlo

Untuk menyelesaikan persamaan-persamaan di atas dengan simulasi Monte Carlo, caranya sangat mudah. Berikut adalah flowchart-nya:

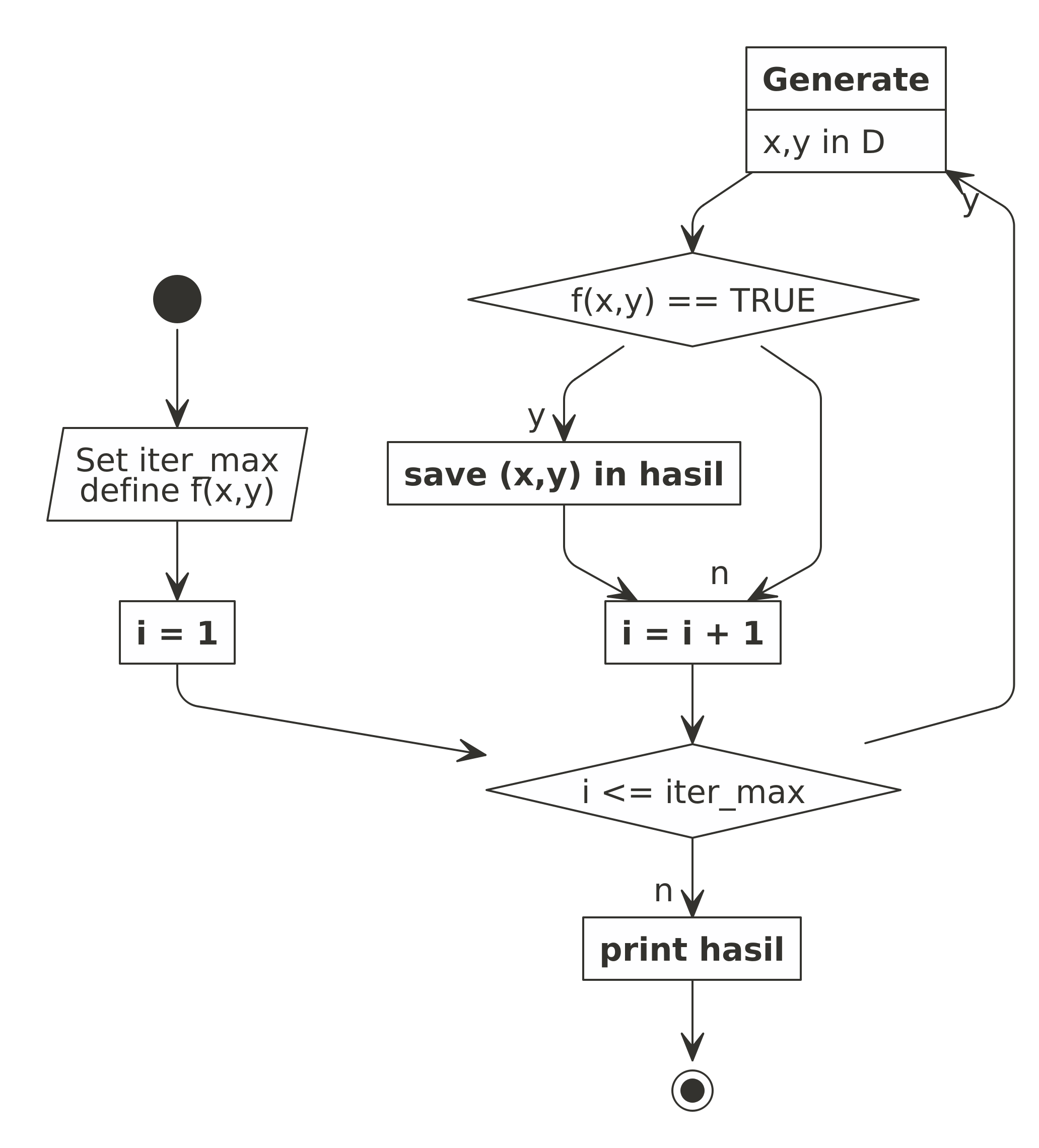
Simpel kan?

Ayo, kita akan coba untuk menyelesaikan empat soal di atas.

---

Soal I

Berikut algoritmanya:

rm(list=ls())
f = function(x,y) {x^2 + y^2}
iter_max = 4000
solusi = data.frame(x = 1,y = 1)
k = 0
for(i in 1:iter_max){
  X = sample(0:25,2,replace=T)
  if(f(X[1],X[2]) == 625){
    solusi[k+1,] = list(X[1],X[2])
    k = k + 1
    }
}

solusi %>% distinct() %>% arrange(x)

##    x  y
## 1  0 25
## 2  7 24
## 3 15 20
## 4 20 15
## 5 24  7
## 6 25  0

Soal II

rm(list=ls())
f = function(x,y) {x^3 + y^3}
iter_max = 4000
solusi = data.frame(x = 1,y = 1)
k = 0
for(i in 1:iter_max){
  X = sample(0:50,2,replace=T)
  if(f(X[1],X[2]) == 1008){
    solusi[k+1,] = list(X[1],X[2])
    k = k + 1
    }
}

solusi %>% distinct() %>% arrange(x)

##   x  y
## 1 2 10

Soal III

rm(list=ls())
f = function(x,y) {x^3 - 3*x*y^2 - y^3}
iter_max = 4000
solusi = data.frame(x = 1,y = 1)
k = 0
for(i in 1:iter_max){
  X = sample(-10:10,2,replace=T)
  if(f(X[1],X[2]) == 1){
    solusi[k+1,] = list(X[1],X[2])
    k = k + 1
    }
}

solusi %>% distinct() %>% arrange(x)

##    x  y
## 1 -3  2
## 2 -1  1
## 3  0 -1
## 4  1 -3
## 5  1  0
## 6  2  1

Soal IV

rm(list=ls())
f = function(x,y,z) {x^2 + y^2 + z^2}
iter_max = 90000
solusi = data.frame(x = 1,y = 1, z = 1)
k = 0
for(i in 1:iter_max){
  X = sample(0:50,3,replace=T)
  if(f(X[1],X[2],X[3]) == 2445){
    solusi[k+1,] = list(X[1],X[2],X[3])
    k = k + 1
    }
}

solusi %>% distinct() %>% arrange(x)

##     x  y  z
## 1   2 29 40
## 2   5 22 44
## 3   5 44 22
## 4   8 34 35
## 5  14 32 35
## 6  14 43 20
## 7  14 20 43
## 8  19 22 40
## 9  20 43 14
## 10 20 37 26
## 11 20 26 37
## 12 22  5 44
## 13 22 44  5
## 14 26 13 40
## 15 26 37 20
## 16 26 40 13
## 17 26 20 37
## 18 29 40  2
## 19 29  2 40
## 20 34 35  8
## 21 35 32 14
## 22 35 14 32
## 23 35 34  8
## 24 37 20 26
## 25 40 22 19
## 26 40  2 29
## 27 43 14 20
## 28 44 22  5

---

if you find this article helpful, support this blog by clicking the ads.