Mengelompokkan Pertanyaan Survey dengan Factor Analysis

Pertama kali saya bekerja di bidang market riset pada 2008, senior-senior saya sering mengatakan bahwa salah satu analisa statistika yang umum digunakan di market riset adalah factor analysis. Namun baru pada 2010 saya bersinggungan langsung dengan analisa tersebut.

Dalam factor analysis (termasuk market riset atau analisa data pada umumnya), ada dua istilah terkait variabel, yaitu:

1. Observed variable, yakni variabel yang diambil datanya dari sumbernya.
2. Latent variable, yakni variabel yang tidak secara langsung diambil datanya namun nilainya didekati dari observed variable lainnya.

Sederhananya, factor analysis digunakan untuk mengelompokkan pertanyaan survey atau variabel data berdasarkan kesamaannya. Ide dasarnya adalah membuat suatu variabel latent yang tidak terobservasi sebagai gabungan dari beberapa variabel terobservasi yang ada.

Masih bingung? Tak mengapa, nanti kita akan bahas pada contoh kasus. hehe

Ada dua jenis factor analysis, yakni:

1. Exploratory factor analysis.
   • Prinsipnya adalah kita belum mengetahui observed variables mana saja yang akan dikelompokkan menjadi latent variables apa saja.
   • Sesuai dengan namanya, yakni exploratory yang berarti eksplorasi atau pencarian.
2. Confirmatory factor analysis.
   • Prinsipnya adalah kita sudah mengetahui observed variables mana saja yang akan dikelompokkan ke dalam beberapa latent variables.

Confirmatory Factor Analysis

Perkenalan saya dengan factor analysis dimulai dengan mengerjakan project Customer Satisfaction and Loyalty Survey (CSLS) untuk salah satu BUMN Telekomunikasi. Teknik yang dipakai adalah membuat Structured Equation Model (SEM) untuk menghitung satisfaction index dan loyalty index.

Jadi kepuasan dan loyalitas pelanggan dihitung menggunakan pertanyaan-pertanyaan tak langsung dari faktor-faktor pembangunnya. Misalkan, kepuasan dari suatu produk bisa didekati dari pertanyaan-pertanyaan 4P (product, placement, promotion, dan price).

Misalkan pada survey tersebut, responden ditanyakan mengenai tingkat kesetujuan dari beberapa pertanyaan tersebut (misalkan pertanyaan ). Maka pertanyaan-pertanyaan tersebut menjadi observed variables. Latent variables sudah didefinisikan sedemikian rupa dan jika digambarkan grafik hubungan, berikut bentuknya:

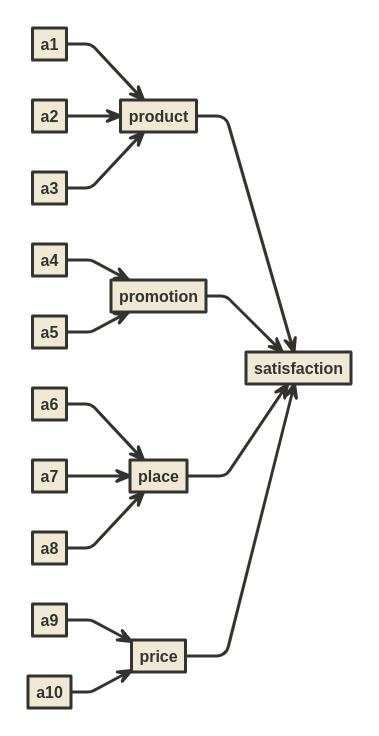
Nanti satisfaction index akan didapatkan dari perkalian persentase top 2 boxes per pertanyaan dengan nilai bobot yang dihasilkan dari confirmatory factor analysis.

Exploratory Factor Analysis

Berbeda dengan CFA, EFA berarti kita sama sekali belum mengetahui hubungan antara satu variabel dengan variabel yang lainnya. Justru kita hendak membuat latent variable(s) dari variabel-variabel yang ada beserta hubungannya.

Misalkan kita melakukan survey berisi delapan buah pertanyaan kepada 100 orang responden, berikut adalah sampel datanya:

   test_1 test_2 test_3 test_4 test_5 test_6 test_7 test_8
1       5      4      3      5      4      4      3      3
2       5      6      4      5      4      5      4      4
3       4      3      3      4      4      3      3      4
4       4      4      4      3      5      4      4      5
5       4      5      2      4      3      4      2      3
6       5      5      5      5      6      5      5      6
7       3      3      4      3      5      3      4      5
8       6      6      5      5      6      5      5      6
9       5      5      4      5      5      4      5      5
10      4      4      4      4      5      4      5      5

Untuk menentukan berapa banyak latent variables dan bagaiman hubungannya, kita bisa membuat terlebih dahulu matriks korelasi. Jangan-jangan kita bisa membuat hipotesis tertentu dari matriks korelasi tersebut.

Jika kita lihat:

1. Pertanyaan saling berkorelasi kuat.
2. Pertanyaan saling berkorelasi kuat.

Kita bisa duga ada dua latent variables yang dibangun dari dua kelompok pertanyaan.

Sekarang kita akan buat EFA-nya dengan dua latent variables:

Call:
factanal(x = df, factors = 2, scores = "regression", rotation = "varimax")

Uniquenesses:
test_1 test_2 test_3 test_4 test_5 test_6 test_7 test_8 
 0.230  0.227  0.174  0.279  0.187  0.166  0.201  0.226 

Loadings:
       Factor1 Factor2
test_1          0.877 
test_2          0.879 
test_3  0.909         
test_4          0.849 
test_5  0.901         
test_6          0.910 
test_7  0.894         
test_8  0.879         

               Factor1 Factor2
SS loadings      3.217   3.092
Proportion Var   0.402   0.387
Cumulative Var   0.402   0.789

Test of the hypothesis that 2 factors are sufficient.
The chi square statistic is 15.18 on 13 degrees of freedom.
The p-value is 0.296 

Perhatikan nilai total proportion var sebesar 0.789 (atau ). Artinya:

About variance in the data is explained by these double factor model.

Masing-masing pertanyaan memiliki bobot tersendiri, yakni:

Loadings:
       Factor1 Factor2
test_1          0.877 
test_2          0.879 
test_3  0.909         
test_4          0.849 
test_5  0.901         
test_6          0.910 
test_7  0.894         
test_8  0.879         

               Factor1 Factor2
SS loadings      3.217   3.092
Proportion Var   0.402   0.387
Cumulative Var   0.402   0.789

Di mana masing-masing pertanyaan hanya unique terpasang ke satu latent variables.

Pertanyaan berikutnya, apakah dua latent variables sudah cukup?

Kita bisa melakukan eksperimen dengan cara melakukan perhitungan ulang dengan membuat banyaknya latent variables bermacam-macam (misalkan dibuat menjadi 3,4, atau 5). Kemudian kita lihat nilai proportion var-nya apakah tetap meningkat signifikan atau justru stabil tak bergerak di range yang sama. Kesimpulannya kelak adalah kita akan pilih banyaknya latent variables yang paling sedikit.

Berikut adalah eksperimennya:

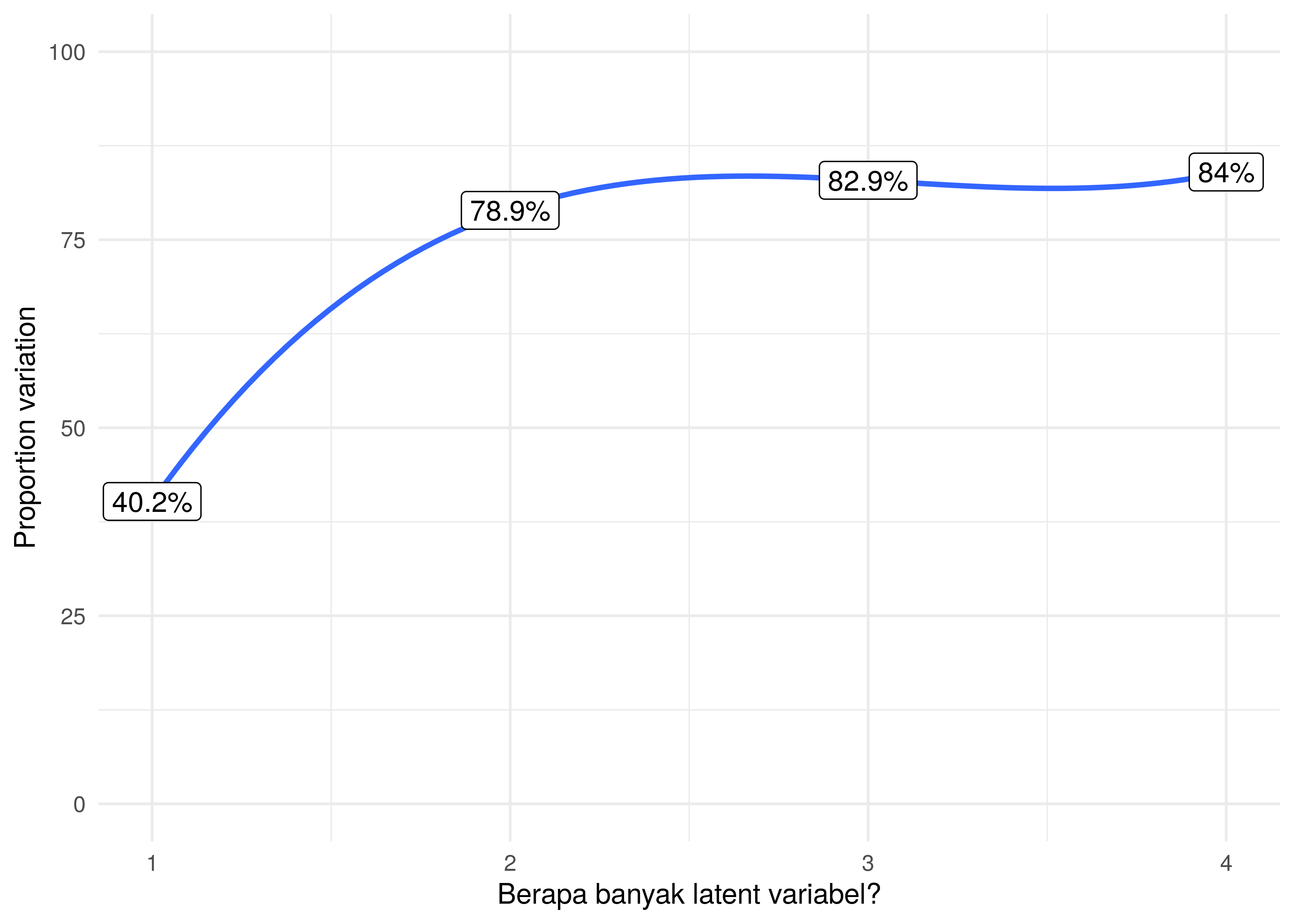
Kita bisa lihat bahwa penambahan latent variables menjadi 3 dan 4 tidak memberikan penambahan yang signifikan.

---

if you find this article helpful, support this blog by clicking the ads.