Bagaimana Menghentikan Hoaks Berdasarkan Model Matematika?

Saat pandemi lalu, saya sedang aktif-aktifnya belajar lagi pemodelan matematika terutama persamaan diferensial untuk memodelkan persebaran virus Covid-19. Setelah pandemi berakhir, saya masih merasa bahwa model seperti ini tetap berguna dan bisa diaplikasikan untuk bidang sosial lainnya.

Sebagai contoh, saya pernah menuliskan tentang model SIR Covid-19. SIR memodelkan kelompok-kelompok orang Susceptible-Infected-Recovered dalam epidemiologi. Model tersebut bisa juga diperuntukkan untuk memodelkan penyebaran hoaks atau informasi palsu. Bagaimana caranya? Cekidot!

---

Model SIR untuk Penyebaran Hoaks

Model ini membagi populasi orang menjadi tiga kelompok utama:

• S (Susceptible): Orang yang belum terpapar hoaks (rentan).
• I (Infected): Orang yang telah terpapar dan menyebarkan hoaks (terinfeksi).
• R (Recovered): Orang yang sudah tahu itu hoaks dan tobat sehingga tidak menyebarkannya ke orang lain (kebal).

Untuk membuat persamaan modelnya, mari kita perhatikan alur logika seperti ini:

Sebagian besar orang di awal waktu masuk ke dalam kelompok rentan. Kemudian muncul orang-orang “terinfeksi” yang mulai menyebarkan hoaks. Sebagian orang yang rentan akan mulai “terinfeksi” dan mulai menyebarkan hoaks tersebut ke orang lain di kelompok rentan. Lambat laun, orang yang “terinfeksi” mulai tobat dan menjadi kebal karena melakukan fact check atau diberikan informasi yang benar oleh pihak lainnya.

Dari cerita di atas, bisa disimpulkan:

1. Kelompok orang rentan berkurang karena termakan hoaks.
2. Kelompok orang “terinfeksi” akan meningkat.
3. Lambat laun, orang “terinfeksi” akan menjadi tobat dan kebal.

Kondisi-kondisi ini bisa ditulis dalam persamaan diferensial sebagai berikut:

}
\frac{dR}{dt} = \gamma \cdot I & \text{(Meningkatnya orang yang “sadar”)} \end{cases}”)

dengan:

• (Tingkat Penularan): Seberapa cepat hoaks menyebar (bergantung pada virality, media sosial, dll.).
• (Tingkat Pemulihan): Seberapa cepat orang menyadari itu hoaks (faktanya terungkap).

Pada model SIR, kita mengenal istilah indeks reproduksi dasar atau .

• Jika , hoaks akan menyebar secara eksponensial (viral).
• Jika , hoaks tidak akan menyebar luas dan segera mereda.

Secara logis, faktor-faktor yang mempercepat penyebaran hoaks antara lain:

• Jaringan Sosial yang Terhubung Erat (Twitter/X, WhatsApp grup, TikTok).
• Emosi Tinggi (konten provokatif, ketakutan, kemarahan).
• Algoritma Media Sosial yang memprioritaskan engagement (like, share, comment).
• Kurangnya Literasi Digital (orang mudah percaya tanpa verifikasi).

Sekarang saya akan melakukan simulasi dengan beberapa nilai parameter berikut ini:

• Populasi = 10.000 orang.
• Awalnya, 1 orang menyebarkan hoaks ().
• atau perubahan waktu didefinisikan sebagai hari.
• (cepat menyebar)
• (hoaks lambat dibantah).
• Maka artinya hoaks akan viral!.

# --------------------------------------
# SIMULASI PENYEBARAN HOAKS (MODEL SIR)
# --------------------------------------

# Paket yang diperlukan
library(deSolve)  # Untuk menyelesaikan persamaan diferensial
library(ggplot2)   # Untuk visualisasi

# 1. Definisi Parameter
N <- 10000         # Total populasi
I0 <- 1            # Kasus awal terinfeksi (hoaks)
S0 <- N - I0       # Susceptible awal
R0 <- 0            # Recovered awal (awalnya belum ada yang sadar)

beta <- 0.4        # Tingkat penularan (seberapa viral hoaks)
gamma <- 0.1       # Tingkat pemulihan (seberapa cepat hoaks dibantah)

waktu <- seq(0, 90, by = 1)  # Rentang waktu (hari)

# 2. Model SIR
sir_model <- function(waktu, state, parameters) {
  with(as.list(c(state, parameters)), {
    dS <- -beta * S * I / N
    dI <- beta * S * I / N - gamma * I
    dR <- gamma * I
    
    return(list(c(dS, dI, dR)))
  })
}

# 3. Solusi Numerik
parameters <- c(beta = beta, gamma = gamma)
state <- c(S = S0, I = I0, R = R0)

solusi <- ode(
  y = state,
  times = waktu,
  func = sir_model,
  parms = parameters
) %>% as.data.frame()

# 4. Visualisasi
ggplot(solusi, aes(x = time)) +
  geom_line(aes(y = S, color = "Susceptible"), linewidth = 1.2) +
  geom_line(aes(y = I, color = "Infected (Hoaks)"), linewidth = 1.2) +
  geom_line(aes(y = R, color = "Recovered (Sadar)"), linewidth = 1.2) +
  labs(
    title = "Dinamika Penyebaran Hoaks (Model SIR)",
    x = "Waktu (hari)",
    y = "Jumlah Orang",
    color = "Kategori"
  ) +
  scale_color_manual(values = c(
    "Susceptible" = "blue",
    "Infected (Hoaks)" = "red",
    "Recovered (Sadar)" = "green"
  )) +
  theme_minimal()

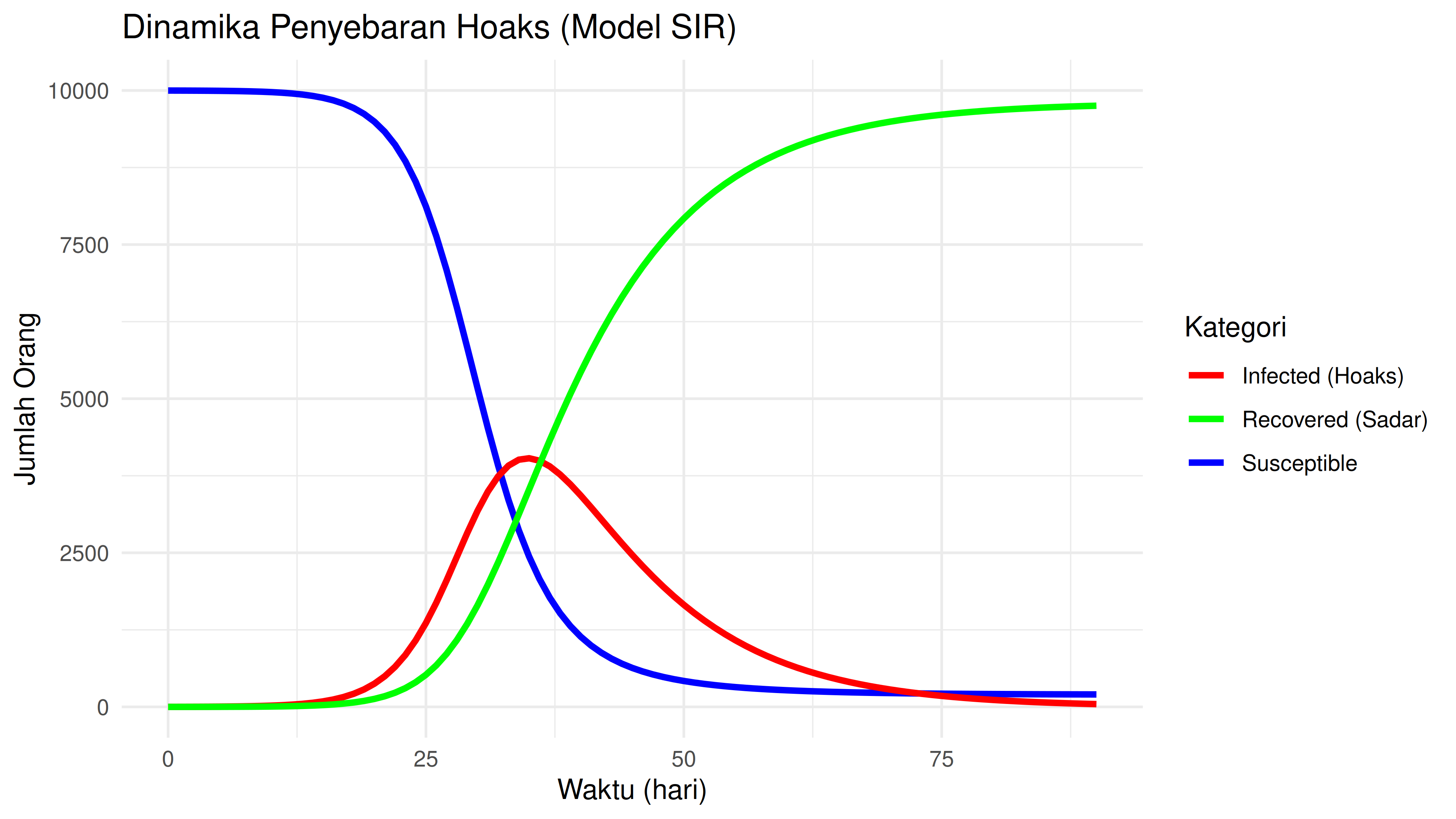
Dari grafik di atas, kita bisa melihat bahwa:

• Fase Eksponensial: Jumlah infected (I) melonjak cepat setelah 20 hari
• Puncak: Saat infected terbanyak kemudian orang mulai sadar ( bekerja).
• Penurunan: Hoaks kehilangan momentum (fakta terungkap).

Di akhir grafik, kita bisa melihat bahwa masih ada sebagian kecil orang di kelompok rentan yang tak terkena hoaks. Sementara mayoritas orang terkena hoaks dan kemudian sadar.

Bagaimana cara “mengobati” penyebaran hoaks? Berdasarkan model:

• Perbesar :
  • Fakta cepat dikoreksi (fact-checking oleh media/komunitas).
  • Edukasi literasi digital.
• Kecilkan :
  • Platform media sosial mengurangi amplifikasi (batas forward di WhatsApp, label peringatan di Twitter).
  • Hukum penyebar hoaks (efek jera).

Sekarang saya akan coba ubah parameternya menjadi sebagai berikut:

• yang berarti hoaks cukup viral.
• yang berarti fakta cepat membantah hoaks.
• yang berarti ada 30 orang yang menyebarkan hoaks di awal periode.

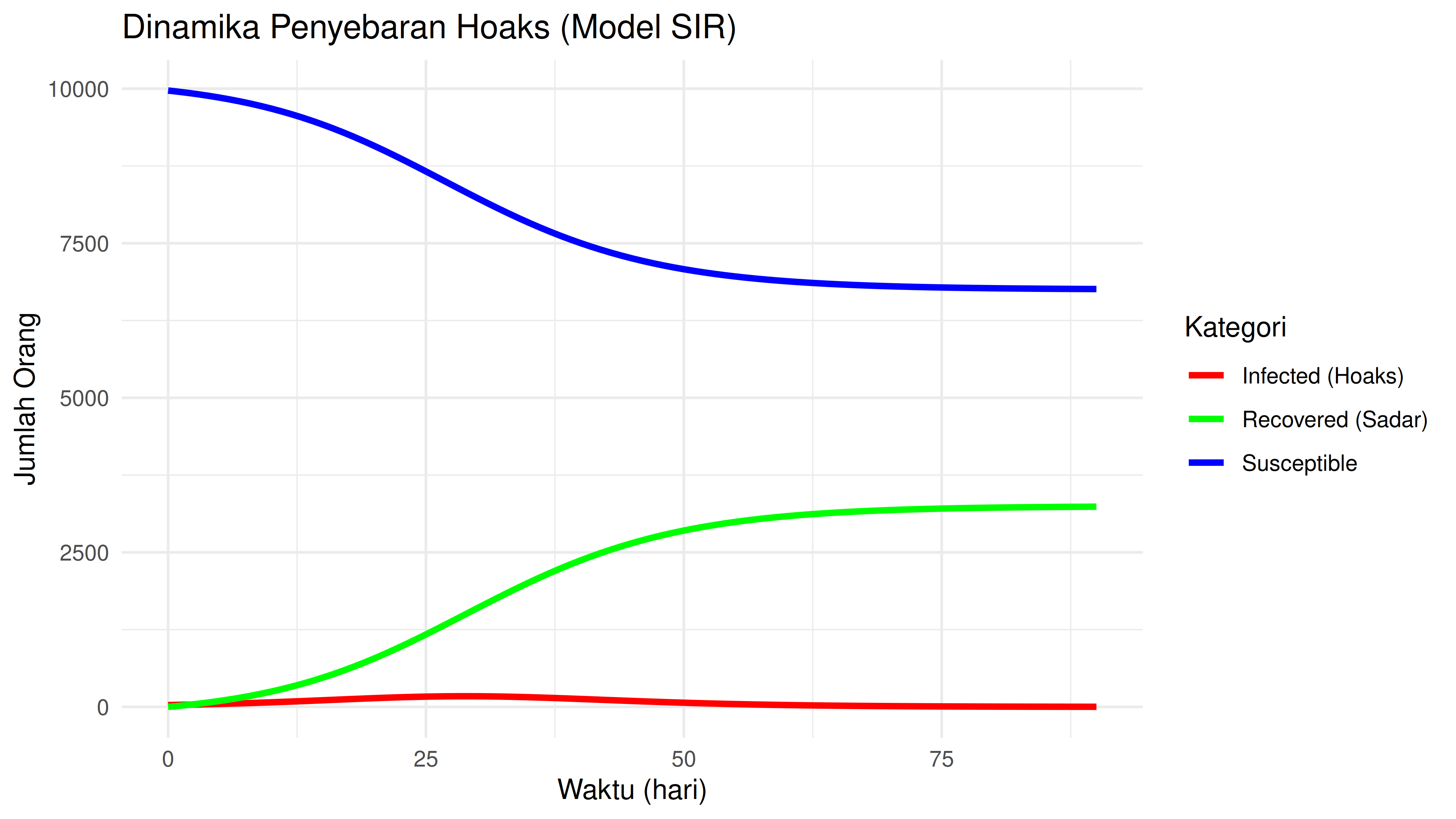
Terlihat bahwa kondisi terkendali dan hoaks tak akan menyebar ke mana-mana.

---

if you find this article helpful, support this blog by clicking the ads.