Mengingat Kembali Uji Hipotesis

Di suatu sore yang cerah, tiba-tiba salah satu aplikasi messaging saya berbunyi. Notifikasi tersebut mengantarkan saya pada seorang teman yang bertanya tentang suatu hal yang sudah lama tidak saya sentuh.

Mas, saya ceritanya saya punya tiga vendor: A, B, dan C. Saya ingin menentukan siapa yang terbaik di antara ketiganya.

Begitu masalah yang ia ingin selesaikan.

Ia bekerja di departemen procurement di salah satu perusahaan FMCG besar di Indonesia.

Lantas saya bertanya:

Apa definisi vendor terbaik?

Ia menjelaskan bahwa definisi vendor terbaik adalah vendor yang memiliki service level paling rendah. Service level adalah banyaknya hari yang dibutuhkan oleh vendor untuk fulfill transaksi yang dijanjikan kepadanya (misalkan lama hari mengirimkan barang kepada perusahaan teman saya).

Jadi teman saya memiliki 200 data service level dari masing-masing vendor tersebut.

service.level.a	service.level.b	service.level.c
3	4	9
5	9	10
7	5	7
7	8	11
2	6	10
2	8	12
6	5	10
5	6	8
9	8	8
4	8	10
7	6	7
1	6	12
3	9	7
2	8	6
6	10	8
10	10	10
6	10	12
10	6	7
3	7	6
5	7	7
2	7	6
3	5	8
9	4	8
9	9	6
9	5	7
7	4	12
6	6	8
3	7	10
10	7	9
2	8	9
5	6	10
6	5	6
1	7	9
5	10	6
3	5	11
1	4	11
6	9	10
10	8	10
3	5	8
5	6	7
1	9	8
5	7	8
8	10	7
9	4	10
9	8	10
6	5	12
6	9	6
5	4	12
6	10	9
9	6	12
10	8	11
5	10	10
2	8	12
8	4	11
1	7	11
8	10	12
9	6	8
4	4	6
6	5	6
3	4	6
7	8	8
1	10	9
6	5	9
6	5	6
9	7	8
3	9	8
3	4	10
8	5	8
8	5	10
2	6	6
1	7	8
3	10	11
8	8	12
9	6	7
4	5	10
4	7	12
3	6	6
10	7	6
10	6	12
5	7	11
2	7	11
1	10	6
10	6	8
7	5	7
4	10	7
6	6	9
2	8	7
3	7	11
5	9	11
8	6	7
2	4	11
8	10	10
6	4	12
2	10	7
2	6	7
10	6	11
1	8	7
4	5	11
2	9	12
6	7	12
5	10	10
4	6	11
6	4	12
5	8	7
10	7	11
10	4	9
4	10	11
10	9	11
3	9	12
9	10	8
1	9	6
9	4	8
3	7	11
2	5	11
5	4	12
8	8	8
8	4	6
5	7	7
5	7	7
8	8	9
9	7	8
10	10	9
5	6	7
5	5	8
8	10	8
1	8	10
7	7	8
5	9	9
4	6	8
10	5	11
2	6	11
1	9	9
3	8	11
7	7	10
3	5	7
6	5	12
6	9	6
4	5	10
7	9	9
10	7	11
6	4	12
3	4	11
10	8	11
7	5	7
3	8	8
4	5	8
3	7	12
3	6	10
6	6	11
5	6	12
1	4	10
8	5	8
1	10	8
5	5	12
5	7	12
6	5	11
3	4	9
6	10	7
2	5	8
7	10	10
4	5	6
4	7	11
6	8	12
6	6	6
10	10	9
6	10	11
1	9	12
4	4	12
10	8	9
1	9	12
1	7	7
5	4	12
2	6	7
4	5	10
1	10	10
6	5	10
9	5	8
7	10	7
6	8	11
4	5	11
5	6	9
3	5	6
9	5	10
5	8	10
10	10	8
2	4	9
8	6	6
3	5	8
1	4	6
10	4	10
1	6	12
10	8	10
10	6	12
2	6	10
4	10	9
8	5	6
8	5	12
3	9	12
1	5	7
5	4	8

Data Service Level Vendor A, B, dan C

Bagaimana cara kita menyelesaikan permasalahan teman saya tersebut?

Statistika Deskripsi

Mari kita lihat terlebih dahulu statistika deskripsi dari data di atas:

##  service.level.a  service.level.b service.level.c 
##  Min.   : 1.000   Min.   : 4.00   Min.   : 6.000  
##  1st Qu.: 3.000   1st Qu.: 5.00   1st Qu.: 7.000  
##  Median : 5.000   Median : 7.00   Median : 9.000  
##  Mean   : 5.305   Mean   : 6.78   Mean   : 9.175  
##  3rd Qu.: 8.000   3rd Qu.: 8.00   3rd Qu.:11.000  
##  Max.   :10.000   Max.   :10.00   Max.   :12.000

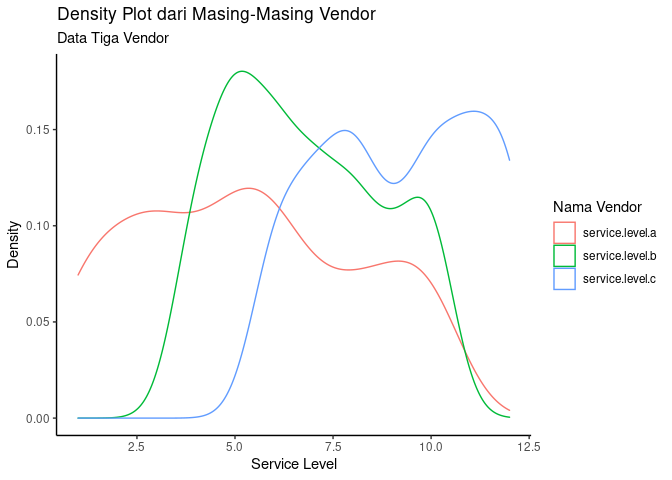
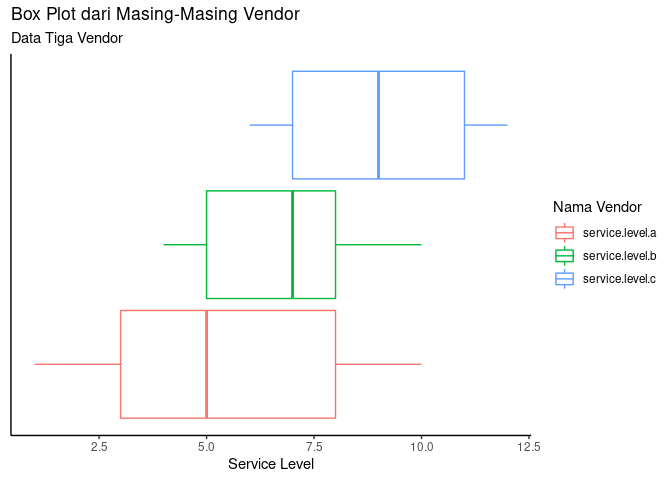
Jika dilihat secara visual, sudah bisa dipastikan bahwa vendor A memiliki nilai rata-rata service level yang paling rendah. Namun perlu dibuktikan, apakah nilai yang rendah tersebut benar-benar signifikan terhadap nilai rata-rata vendor lainnya (B dan C).

Maka yang perlu dicek adalah pasangan data sebagai berikut:

1. A vs B
2. A vs C
3. B vs C

---

Uji Hipotesis

Kita bisa melakukan uji hipotesis untuk mengecek apakah ada perbedaan yang signifikan dari nilai rata-rata tersebut. Langkah-langkah dalam uji hipotesis adalah:

1. Tentukan hipotesis nol dan hipotesis tandingan.

• Notasi: dan
• Hipotesis nol adalah hipotesis yang mengandung unsur sama dengan.

1. Hitung statistik uji atau p-value.
2. Kesimpulan: Tolak jika p-value < 0.05.
3. Tuliskan kesimpulan dengan kalimat non matematis.

Dalam statistika inferensi, ada dua pendekatan yang bisa ditempuh, yakni:

1. Statistika parametrik. Syarat: data harus berdistribusi normal.
2. Statistika non parametrik. Syarat: data tidak harus berdistribusi normal.

Untuk kasus ini, kita akan menggunakan T-Test (jika parametrik) atau Wilcox Test (jika non parametrik). Oleh karena itu, langkah pertama yang harus ditempuh adalah dengan mengecek normalitas dari ketiga data tersebut.

Cek Normalitas dari Data

Beberapa literatur menyebutkan bahwa normality check adalah hal yang wajib dilakukan sebelum kita hendak melakukan uji parametrik. Namun, beberapa literatur lainnya tidak mewajibkan hal tersebut jika dataset yang kita miliki sudah relatif banyak sehingga cukup dengan Central Limit Theorem, dataset yang kita miliki sudah bisa diasumsikan normal.

Sebenarnya untuk urusan begini, saya agak males yah. Hahaha. Tapi yuk kita coba cek normalitas dari ketiga data tersebut.

Sesuai dengan post saya sebelumnya, saya akan menggunakan uji kenormalan Kolmogorov-Smirnov.

Oh iya, cek normalitas juga merupakan uji hipotesis, maka langkah-langkah yang harus ditempuh:

1. Tentukan hipotesis nol dan tandingan:

• : Data berdistribusi normal.
• : Data tidak berdistribusi normal.

1. Hitung p-value dan lihat bagaimana hasilnya.

test.a = ks.test(data$service.level.a,'pnorm')
test.b = ks.test(data$service.level.b,'pnorm')
test.c = ks.test(data$service.level.c,'pnorm')

hasil = data.frame(
  vendor = c('A','B','C'),
  p_value = c(test.a$p.value,test.b$p.value,test.c$p.value)
) %>% 
  mutate(kesimpulan = ifelse(p_value < 0.05,'Tolak H0','H0 diterima'),
         hasil_akhir = ifelse(p_value < 0.05,'Tidak berdistribusi normal','Berdistribusi Normal'))

knitr::kable(hasil)

vendor	p_value	kesimpulan	hasil_akhir
A	0	Tolak H0	Tidak berdistribusi normal
B	0	Tolak H0	Tidak berdistribusi normal
C	0	Tolak H0	Tidak berdistribusi normal

Ternyata didapatkan bahwa ketiga data vendor tersebut tidak berdistribusi normal. Oleh karena itu, saya akan menggunakan uji non parametrik untuk menyelesaikan permasalahan ini.

Wilcoxx Tes dari Pasangan Data Vendor

Sebagaimana yang telah saya infokan, saya akan melakukan tiga kali tes dari pasangan data yang ada. Mari kita lakukan langkah-langkah uji hipotesis berikut ini:

1. Tentukan hipotesis nol dan tandingan:

• : Rata-rata service level = rata-rata service level
• : Rata-rata service level rata-rata service level

1. Hitung p-value dan lihat bagaimana hasilnya.

test_1 = wilcox.test(data$service.level.a,data$service.level.b)
test_2 = wilcox.test(data$service.level.a,data$service.level.c)
test_3 = wilcox.test(data$service.level.b,data$service.level.c)

hasil = data.frame(
  vendor_1 = c('A','A','B'),
  vendor_2 = c('B','C','C'),
  p_value = c(test_1$p.value,test_2$p.value,test_3$p.value)
) %>% 
  mutate(kesimpulan = ifelse(p_value < 0.05,'Tolak H0','H0 diterima'),
         hasil_akhir = ifelse(p_value < 0.05,
                              paste0(vendor_1,' tidak sama dengan ',vendor_2),
                              paste0(vendor_1,'=',vendor_2)))

knitr::kable(hasil)

vendor_1	vendor_2	p_value	kesimpulan	hasil_akhir
A	B	1e-07	Tolak H0	A tidak sama dengan B
A	C	0e+00	Tolak H0	A tidak sama dengan C
B	C	0e+00	Tolak H0	B tidak sama dengan C

Kesimpulan

Dari hasil diatas, kita telah mendapati bahwa:

1. A B
2. A C
3. B C

Jika dilihat kembali dari grafik boxplot sebelumnya, kita bisa simpulkan bahwa:

---

Masalah Belum Selesai

Setelah saya sampaikan temuan saya ini, teman saya lantas berkata:

Jika Vendor A adalah yang terbaik, apakah vendor tersebut sudah memenuhi standar service level perusahaan saya?

Teman saya menginformasikan bahwa standar service level perusahaannya adalah 4 hari. Jadi sekarang tugas kita adalah mengecek apakah mean(service.level.a) < 5.

Berhubung datanya tidak normal, saya akan tetap menggunakan Wilcox Test untuk satu sampel. Mari kita lakukan langkah-langkah uji hipotesis berikut ini:

1. Tentukan hipotesis nol dan tandingan:

• : Rata-rata service level vendor A 5 hari
• : Rata-rata service level vendor A < 5 hari

1. Hitung p-value dan lihat bagaimana hasilnya.

test = wilcox.test(data$service.level.a, mu = 5, alternative = "less")
test

## 
##  Wilcoxon signed rank test with continuity correction
## 
## data:  data$service.level.a
## V = 8562, p-value = 0.9244
## alternative hypothesis: true location is less than 5

Ternyata didapatkan hasil p-value = 0.9244477.

Kesimpulan: H0 diterima alias Vendor A masih berada di atas standar perusahaan teman saya.