Bunch of Ideas, a little bit of Maths.

I am mathematician doing market research and data science

5 minute read

Sepertinya sudah lama saya tidak menulis lagi karena riweuh di kantor dan kuliah.

Untuk membuka kembali niat untuk menulis, saya akan bercerita tentang salah satu metode aproksimasi (hampiran) yang bisa digunakan untuk menghitung nilai integral tentu di matematika.

Sebelumnya, saya pernah menulis tentang cara menghitung nilai \pi dengan dua cara:

  1. Melempar darts ala Simulasi Monte Carlo.
  2. Membuat pendekatan trapezoid dari fungsi seperempat lingkaran.

Nah, cara ketiga ini merupakan modifikasi atau gabungan dari keduanya.

Lho kok bisa?

Jadi saya akan gunakan prinsip Monte Carlo untuk generate random points di selang integral tentu lalu menggunakan pendekatan luas square seperti halnya trapezoid.

Sebagai contoh, saya akan menyelesaikan soal berikut:

Hitunglah:

f(x) = \int_2^3 (x^2 + 4x \sin{x}) dx

Jika kita hendak mencari solusi analitiknya, sepertinya agak susah yah. hehe (atau saya saja yang cenderung malas)

Solusi analitik dari f(x) = \int (x^2 + 4x \sin{x}) dx adalah:

F(x) = \frac{x^3}{3} - 4x \cos{x} + 4 \sin{x}

Sehingga:

\int_2^3 (x^2 + 4x \sin{x}) dx \approx 11.811358925

Oleh karena itu ada metode aproksimasi yang relatif lebih mudah dilakukan (menurut saya).

Ide dari algoritma ini adalah men-generate titik random di selang integral, kemudian dihitung luas square yang ada.

Perhatikan bahwa titik yang di-generate adalah pada sumbu x (selang integral) saja. Berbeda dengan darts yang memerlukan random di sumbu x dan y.

Sehingga:

I = \int_z^b f(x)dx

dihitung sebagai:

<F^N> = \frac{b-a}{N+1} \sum_{i=0}^N f(a + (b-a) \xi_i)

dengan

\xi_i \text{ adalah random number antara 0 dan 1}

Berikut adalah flowchart-nya:

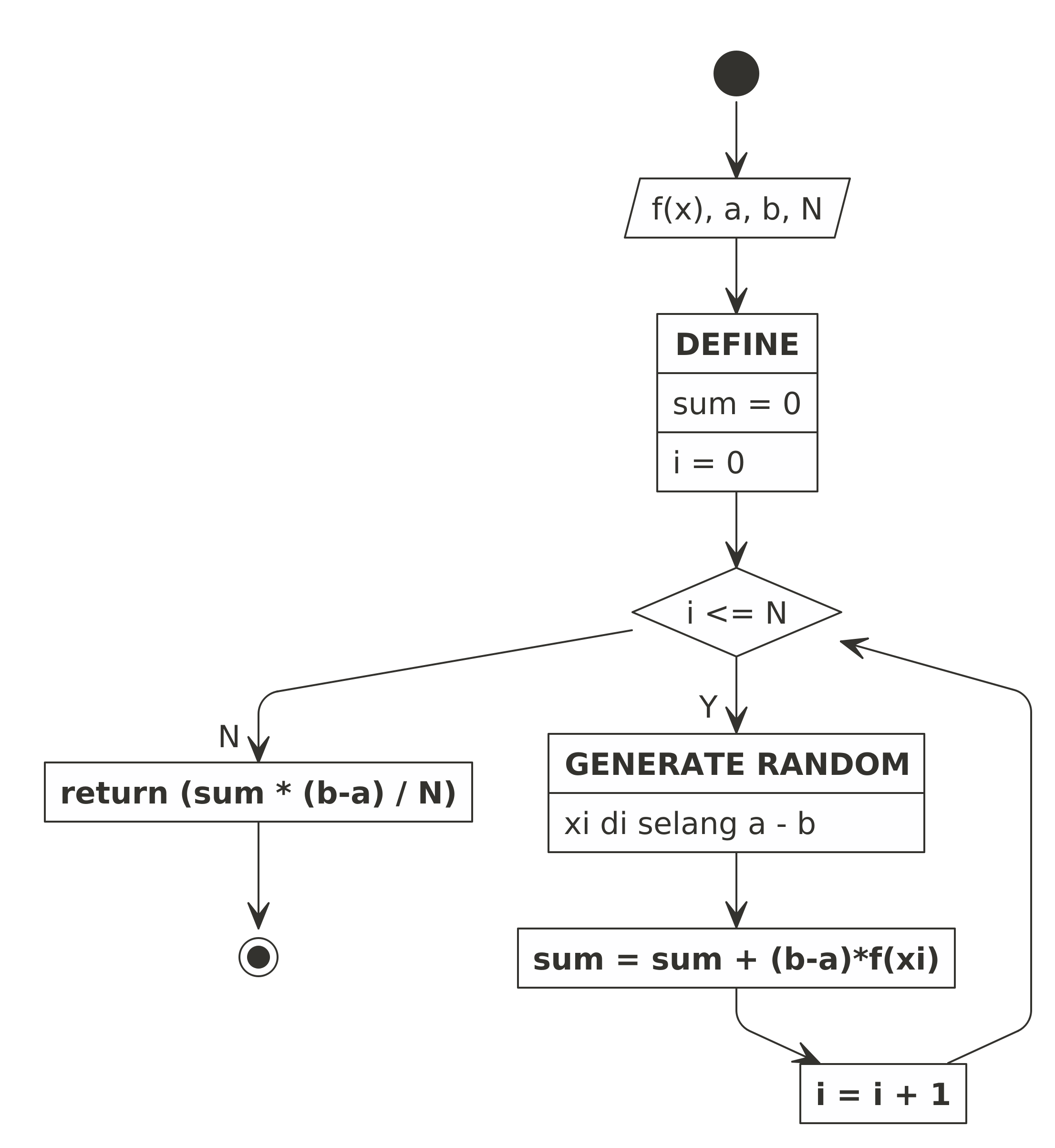
Flowchart Modifikasi Monte Carlo

Flowchart Modifikasi Monte Carlo

Berdasarkan flowchart di atas, berikut adalah function di R -nya:

modif_monte = function(f,x1,x2,N){
  # set template terlebih dahulu
  hasil = c()
  
  # kita akan ulang proses ini 100 kali untuk N titik
  for(ikang in 1:100){
    # generating random number
    x = runif(N,x1,x2)
    # hitung f(x)
    f_x = f(x)
    # hitung luas
    luas = (x2-x1) * f_x
    mean_luas = mean(luas)
    hasil[ikang] = mean_luas
  }
  # mean luas
  output = mean(hasil)
  # output
  return(output)
  }

Simple kan?

Oke, sebelum menyelesaikannya dengan fungsi di atas, saya akan berikan ilustrasi sebagai berikut:

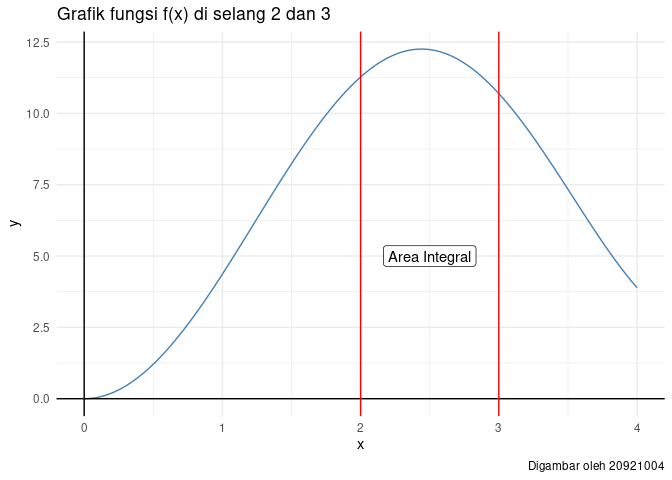
Di atas adalah grafik dari f(x). Metode ini bertujuan untuk men-generate satu random titik di antara selang [2,3] (misal saya tuliskan sebagai x_i kemudian dihitung nilai f(x_i).

Contoh:

Saya akan generate satu titik sebagai berikut:

Dari titik tersebut, saya akan buat garis sehingga terbentuklah sebuah square:

Kelak kita akan menghitung luas dari square tersebut.

Semakin banyak kita generate titiknya, kita bisa menghitung rata-rata luas dari squares tersebut. Nilai rata-rata tersebut akan dijadikan hampiran integral tentu.

Berikut adalah nilai hampirannya untuk berbagai banyak titik yang di-generate:

N Solusi Aproksimasi Selisih dengan Nilai Eksak
10 11.78907 0.0222857
100 11.80707 0.0042907
500 11.81512 0.0037561
750 11.81119 0.0001678
1000 11.81079 0.0005681
5000 11.81043 0.0009298
7500 11.81094 0.0004159
10000 11.81127 0.0000927
25000 11.81206 0.0007033
50000 11.81161 0.0002520
100000 11.81105 0.0003059
250000 11.81138 0.0000242
500000 11.81129 0.0000719
750000 11.81142 0.0000590

Hasil Perbandingan Solusi Numerik dan Eksak

Untuk setiap banyak titik, prosesnya saya ulangi hingga 100 kali agar lebih konvergen ke hasilnya.

Terlihat bahwa nilai hampirannya sudah sangat dekat dengan nilai eksaknya.

if you find thsi article helpful, support this blog by clicking the ads.

You May Also Enjoy