Mencari Simmilarity dan Dissimilarity dari Data
Pada tahun lalu, saya pernah menulis tentang bagaimana menemukan persamaan dan perbedaan dari data phonebook agar kita bisa menemukan beberapa entry ganda yang ada. Pada tulisan tersebut, saya menggunakan algoritma yang berdasarkan cosine simmilarity.
Kali ini saya akan membahas lebih detail apa yang disebut dengan persamaan dan pertaksamaan.
Simmilarity Vs Dissimilarity
Prinsip sederhana yang digunakan untuk mengukur apakah dua data itu sama atau tidak adalah dengan mengukur jarak antar kedua data tersebut.
Data
dan
disebut sama jika jarak antar keduanya
.
Pada tulisan terdahulu, saya pernah membedah berbagai macam tipe dan struktur data. Masing-masing tipe dan struktur data mmemiliki cara perhitungan jaraknya tersendiri. Kita bahas satu-persatu berikut ini:
Data Numerik
Misalkan saya punya dua titik numerik sebagai berikut:
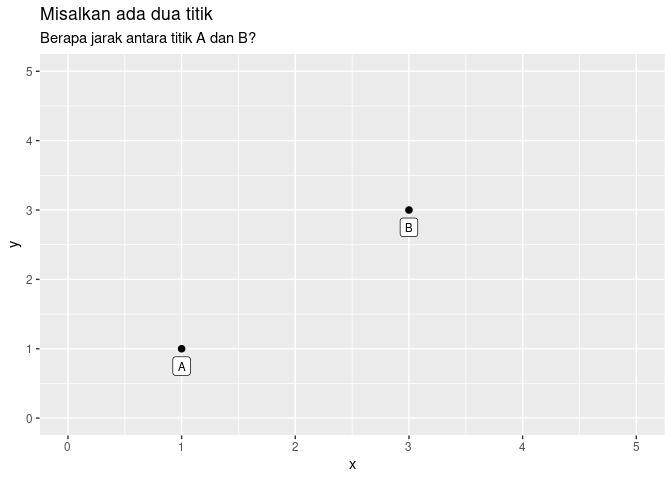
Untuk data numerik, ada beberapa perhitungan jarak seperti:
Euclidean distance
Yakni jarak terpendek antara dua titik. Cara perhitungannya adalah dengan menggunakan rumus Phytagoras.
Dari dua titik di atas kita hitung jaraknya sebagai berikut:
Manhattan distance
Yakni jarak total yang dimiliki dari masing-masing dimensinya. Misalkan
dari dua titik di atas, kita akan menghitung jarak di masing-masing
sumbu dan sumbu
-nya.
|  = | x_1 - x_2 | + | y_1 - y_2 | ”) |
Dari dua titik di atas kita hitung jaraknya sebagai berikut:
Chebyshev distance
Yakni jarak terjauh dari dua titik berdasarkan masing-masing dimensinya.
Kita hanya akan cari nilai jarak terjauh dari sumbu
atau sumbu
.
|  = \max{ | (x_1 - x_2) | , | (y_1 - y_2) | }”) |
Pada kasus ini, jarak baik di sumbu
dan
adalah sama-sama
.
Selain ketiga metode di atas, ada berbagai macam cara perhitungan jarak lain yang bisa digunakan.
Data Kategorik
Jika pada bagian di atas, kita telah membahas perhitungan jarak pada data numerik. Bagaimana jika kita memiliki data kategorik? Hal yang sama bisa juga digunakan untuk data non-numerik seperti data teks.
Misalkan, saya hendak mencari jarak dari data berikut ini:
| orang | hobi |
|---|---|
| 1 | masak,nonton |
| 2 | masak,otomotif |
Seberapa mirip kedua orang tersebut? Bagaimana mengukur jarak mereka?
Kita ubah terlebih dahulu kedua data tersebut menjadi bentuk kategorik dan binary. Setelah itu, kita bisa mengukur jarak antara keduanya.
Ubah datanya dalam bentuk seperti ini:
| orang | masak | nonton | otomotif |
|---|---|---|---|
| 1 | 1 | 1 | 0 |
| 2 | 1 | 0 | 1 |
Setelah itu, kita bisa ukur dengan beberapa cara perhitungan jarak.
# dataset yang digunakan
df_new
## orang masak nonton otomotif
## 1 1 1 1 0
## 2 2 1 0 1
# kita simpan dulu beberapa variabel penting
hobi_1 = df_new$masak[2] - df_new$masak[1]
hobi_2 = df_new$nonton[2] - df_new$nonton[1]
hobi_3 = df_new$otomotif[2] - df_new$otomotif[1]
Euclidean distance
jarak_ecl = sqrt(hobi_1^2 + hobi_2^2 + hobi_3^2)
jarak_ecl
## [1] 1.414214
Manhattan distance
jarak_man = hobi_1 + hobi_2 + hobi_3
jarak_man
## [1] 0
Chebyshev distance
jarak_che = max(hobi_1,hobi_2,hobi_3)
jarak_che
## [1] 1
Kelak perhitungan jarak ini adalah kunci untuk menentukan seberapa mirip atau tidak mirip sepasang data.
Bagaimana mudah kan?
if you find this article helpful, support this blog by clicking the ads.
