Menentukan Apakah Suatu Data Fluktuatif atau Tidak?

Pada pagi hari ini:

Salesperson : “Mas, bagaimana ya caranya agar saya bisa menentukan suatu data itu fluktuatif atau tidak?”

Saya : “Fluktuatif yang kamu maksud itu variability?”

Salesperson : “Bukan tentang sebaran data. Maksudnya adalah bagaimana cara menentukan data itu bergerak naik turun secara ekstrim.”

Saya : “Boleh dijelaskan lagi seperti apa maksudnya?”

Salesperson : “Misalkan saya punya data *sales harian selama 2 bulan. Produk A rata-ratanya 150 pcs dan standar deviasinya juga 100 pcs. Lalu produk B dengan rata-rata 1000 pcs dan standar deviasinya juga 100 pcs. Produk A kan seharusnya lebih fluktuatif yah dibanding produk B?”*

Saya : “Ooh, saya mengerti maksudnya. Jadi begini…..”

---

Begitu kira-kira percakapan antara saya dan salah seorang rekan kerja yang berasal dari divisi sales. Sebuah pertanyaan yang tidak mudah, pikir saya.

Untuk menyelesaikan permasalahan tersebut, mari kita lihat terlebih dahulu dua konsep sederhana dalam statistika yakni:

1. Pemusatan data (centrality) dan
2. Sebaran data (variability).

Sesuai dengan namanya, centrality adalah suatu pengukuran untuk menentukan dimana data tersebut berpusat (atau berkumpul). Kita bisa menghitung 3 metrics pada centrality, yakni mean, median, dan modus.

Variability adalah suatu pengukuran yang menentukan seberapa data tersebar. Ada beberapa metric yang bisa dihitung seperti: variansi, standar deviasi, dan range.

Masalah yang ditemui oleh rekan saya itu adalah:

Bagaimana menentukan suatu data itu fluktuatif atau tidak?

Awalnya saya menjawab hanya dengan mengandalkan variability. Namun setelah saya pikirkan kembali, saya akan kehilangan informasi yang sangat penting jika semata hanya mengandalkan variability. Oleh karena itu saya harus menyandingkannya dengan di mana data tersebut terpusat.

Sebagai contoh, saya akan gunakan data sales produk A dan B ilustrasi yang diberikan teman saya berikut ini:

Ilustrasi

Misalkan saya memiliki data sales harian dua produk selama 2 bulan berdistribusi normal:

1. Produk A: .
2. Produk B: .

hari_ke	A	B
1	-15.0	1053.9
2	92.5	923.3
3	64.9	906.2
4	87.7	1012.5
5	-75.3	1012.3
6	99.0	978.8
7	68.8	721.3
8	60.3	878.4
9	89.9	850.1
10	239.5	995.3
11	238.8	1128.9
12	0.8	999.6
13	172.7	1117.6
14	100.2	909.0
15	118.7	971.8
16	277.0	901.3
17	175.2	1009.1
18	81.0	975.6
19	228.5	960.3
20	136.9	945.3
21	334.8	1143.7
22	108.7	905.2
23	50.7	1038.6
24	212.9	1012.2
25	83.9	1073.1
26	107.3	1058.1
27	120.6	771.1
28	184.0	862.5
29	182.0	958.7
30	158.2	822.6
31	97.3	1157.9
32	231.2	1042.7
33	307.0	923.6
34	101.0	1034.4
35	118.2	1060.4
36	139.2	1075.4
37	-91.4	1157.8
38	75.9	1031.9
39	211.4	1178.2
40	170.9	999.6
41	126.0	915.5
42	213.6	893.3
43	101.2	1132.7
44	64.6	1024.4
45	187.0	785.3
46	234.5	1206.0
47	-14.6	855.4
48	95.2	1155.1
49	-42.3	946.5
50	167.0	1236.4
51	18.1	904.6
52	151.3	989.6
53	140.0	1057.9
54	88.3	929.5
55	40.6	1103.9
56	42.6	929.6
57	171.1	985.9
58	372.7	939.0
59	134.5	990.6
60	-14.4	1044.6

Jika saya gambarkan dalam bentuk density plot, kita dapatkan bentuk seperti ini:

Terlihat dari plot di atas, keduanya punya variability yang sama. Jika hanya bermodalkan informasi tersebut, saya hanya akan mengatakan bahwa kedua produk tersebut memiliki fluktuasi yang sama.

Namun saat saya melihat kembali data tersebut dalam bentuk linechart sebagai berikut:

Lalu saya coba samakan sumbu y kedua grafik tersebut:

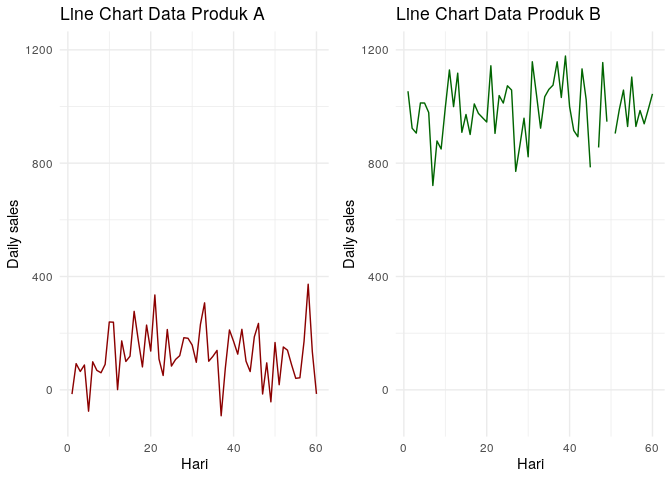
Saya mulai berpikir, jangan-jangan produk A lebih berfluktuasi daripada produk B.

Kenapa?

Pada produk A kita dapati bahwa nilai sales-nya bergerak naik dan turun secara “ekstrim”. Maksudnya adalah nilai sales-nya kadang berada di nilai nol, kadang melebihi jauh dari rata-ratanya. Hampir tidak ada kepastian bahwa ada sales di suatu hari tertentu.

Sedangkan produk B, walaupun bergerak naik dan turun dalam range yang sama dengan produk A, tapi pergerakan sales-nya masih pada nilai yang tinggi dan relatif “aman”.

Koefisien Variasi

Beberapa saat kemudian, saya mulai mengingat kembali salah satu rasio yang biasa digunakan dalam statistika yang berguna untuk melihat sebaran data dari rata-rata hitungnya. Rasio tersebut disebut sebagai koefisien variasi.

Formulanya adalah sebagai berikut:

Semakin kecil rasio koefisien variasi, maka kita bisa simpulkan bahwa data semakin homogen. Sementara sebaliknya, semakin besar nilai rasionya maka data akan semakin heterogen.

Kembali ke masalah rekan saya ini, sepertinya bisa diselesaikan dengan menghitung koefisien variasi.

Kalau kita hitung:

# koefisien variasi produk A
mean = 150
sd = 100
sd/mean * 100 

## [1] 66.66667

# koefisien variasi produk B
mean = 1000
sd = 100
sd/mean * 100

## [1] 10

Kita dapatkan bahwa koefisien variasi produk A adalah sebesar 66.67% sedangkan produk B sebesar 10%. Artinya produk A lebih heterogen (atau dalam masalah rekan saya ini lebih berfluktuasi) dibandingkan produk B.

---

if you find this article helpful, support this blog by clicking the ads