Optimization Story: Menentukan Letak Pool Taxi dengan Mixed Integer Linear Programming

Beberapa waktu lalu, saya dan beberapa rekan di kantor berdiskusi ringan mengenai data spasial (longlat location).

Apa sih faedahnya jika kita memiliki data spasial?

Ada beberapa hal yang bisa kita lakukan. Salah satunya adalah menentukan rute terbaik dengan algoritma TSP. Tapi ada satu hal yang belum pernah lakukan. Apa itu?

Sekarang saya akan mengawinkan antara optimisasi mixed integer linear programming dengan analisa spasial.

Optimisasi ini bisa digunakan untuk berbagai macam kasus, tapi kali ini saya akan menggunakan kasus yang umum terjadi saja yah. Nanti jika ada kasus berbeda tapi mirip-mirip cara berpikirnya, kita tinggal mengubah formulasi matematikanya saja.

---

Problem

Suatu perusahaan taxi sedang mempertimbangkan untuk membangun beberapa pool taxi untuk mendekatkan mereka kepada konsumen-konsumennya. Mereka memiliki data lokasi-lokasi mana saja memiliki high demand terhadap taxi mereka.

Tercatat ada 200 buah lokasi yang memiliki high demand. Mereka juga telah melakukan survey terhadap 40 buah calon lokasi pool taxi. Masing-masing calon lokasi pool taxi tersebut memiliki harga sewa yang beragam.

Berikut adalah biaya yang dibutuhkan untuk menyewa dan me-maintain masing-masing calon lokasi pool taxi tersebut:

## Tabel Biaya yang Akan Dikeluarkan

id_calon_pool	total_biaya
1	320
2	450
3	390
4	300
5	380
6	420
7	430
8	430
9	450
10	340
11	340
12	450
13	430
14	450
15	350
16	450
17	400
18	310
19	340
20	430
21	340
22	430
23	370
24	380
25	390
26	400
27	440
28	310
29	430
30	310
31	410
32	380
33	340
34	440
35	310
36	390
37	430
38	330
39	370
40	420

Permasalahannya:

Perusahaan taxi tersebut memiliki budget dan sumber daya terbatas. Oleh karena itu mereka perlu mencari berapa jumlah pool taxi yang seminimum mungkin tapi tetap covering area-area high demand tersebut.

Formulasi Matematika

Oke, sekarang saya mulai bagian serunya. Inti permasalahan ini sebenarnya adalah:

Memasangkan lokasi-lokasi high demand secara optimal dengan beberapa calon lokasi pool taxi.

Misalkan menandakan banyaknya lokasi high demand, .

Sedangkan menandakan berapa banyak calon lokasi pool taxi .

Lalu merupakan bilangan biner (0,1) yang menandakan:

• 0 jika lokasi high demand ke tidak dipasangkan dengan calon lokasi pool taxi ke .
• 1 jika lokasi high demand ke dipasangkan dengan calon lokasi pool taxi ke .

Lalu merupakan bilangan biner (0,1) yang menandakan:

• 0 jika calon lokasi pool taxi ke tidak perlu disewa.
• 1 jika calon lokasi pool taxi ke perlu disewa.

Constraints

Kita ketahui bahwa satu lokasi high demand hanya boleh di-cover oleh satu pool taxi saja.

untuk .

Lalu saat ada lokasi high demand yang di-cover oleh pool (), maka pool harus dibangun ().

Objective Functions

Setidaknya ada dua kondisi yang kita wajibkan agar pemilihan pool ini optimal:

1. Total jarak antara pool dan lokasi-lokasi high demand yang di-cover olehnya harus terpendek. Kenapa? Semakin jauh, maka transportation cost yang dikeluarkan juga semakin besar.
2. Total biaya sewa yang dikeluarkan untuk pool harus paling minimum.

Maka saya tuliskan objective functions sebagai berikut:

Transportation cost saya definisikan sebagai jarak antara calon lokasi pool dengan lokasi high demand dikalikan suatu konstanta tertentu.

Solusi

Solusi dari formula matematika di atas adalah sebagai berikut:

## Solusi Optimisasi

pool_id	banyak_high_demand_covered	cost_sewa	total_transport_cost
1	7	320	1290.03
3	5	390	409.31
7	13	430	2371.28
8	12	430	1847.07
10	11	340	2113.65
11	7	340	828.82
14	7	450	658.13
15	8	350	1088.55
16	12	450	1984.10
18	6	310	1011.67
22	7	430	819.03
23	4	370	320.77
24	11	380	1626.81
25	8	390	752.31
26	6	400	539.92
30	6	310	833.44
36	13	390	1927.21
37	8	430	1002.10
39	9	370	1233.63

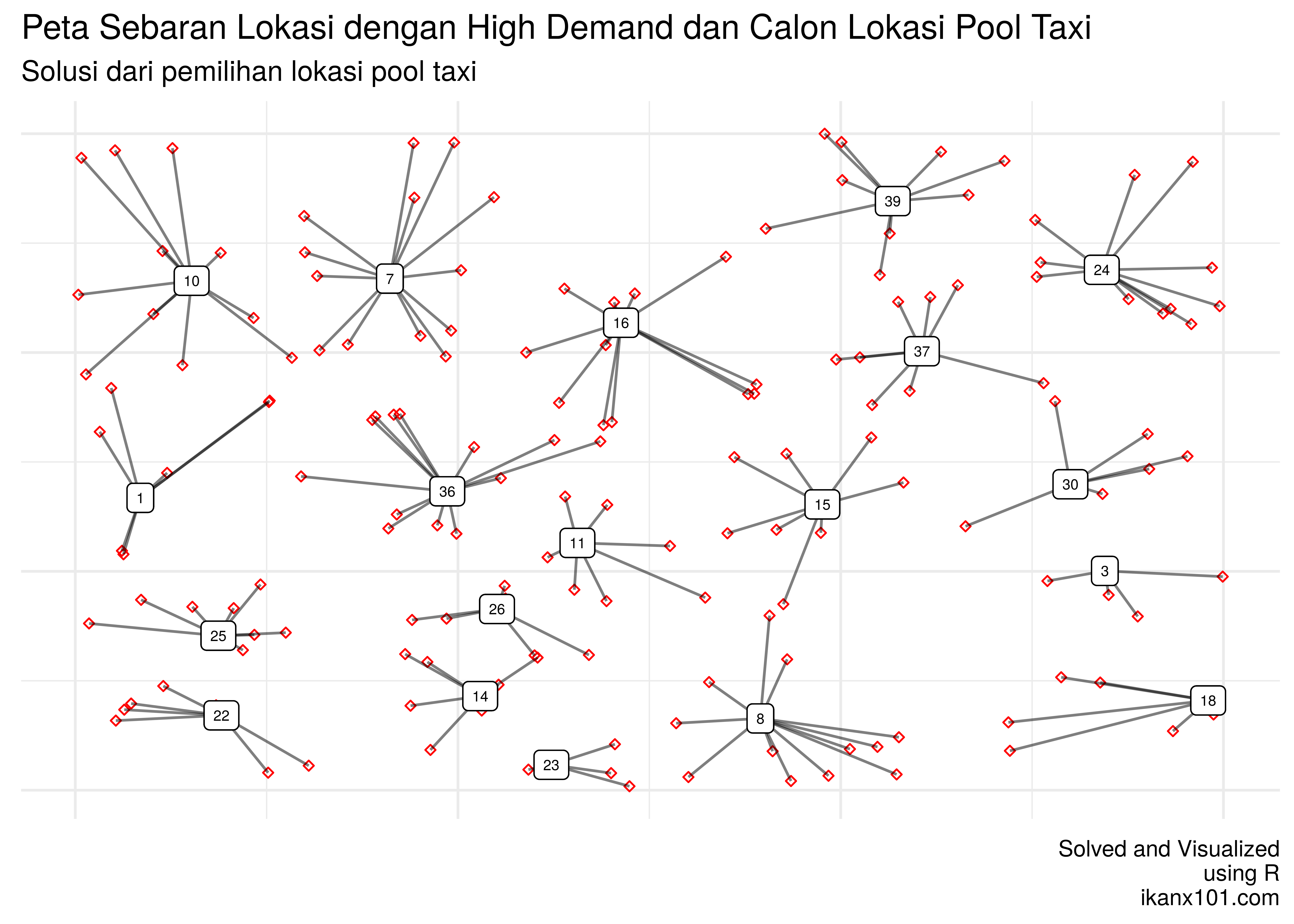
Ternyata cukup dibutuhkan 19 calon pool taxi saja yang harus disewa dengan total cost sebagai berikut:

• Total cost sewa: 62160.
• Total transportation cost: 22657.83.

Mari kita lihat peta finalnya:

---

What’s next?

Kita bisa melakukan another tweaks jika diperlukan. Misalkan kita tambahkan syarat agar satu pool taxi wajib meng-cover sejumlah minimal lokasi high demand.