Melukis Fungsi Matematika dengan ggplot

Selama kuliah ini, saya jadi sering bertemu dengan fungsi matematika. Sebagian besar dari fungsi tersebut harus dibuat grafiknya agar terlihat bagaimana karakteristik dan polanya. Fungsi yang saya maksud di sini masih terbatas 2 dimensi yah. Jadi bisa digambarkan dalam bidang katesian (sumbu x dan y). Untuk fungsi dengan peubah yang lebih banyak akan saya bahas di kemudian hari.

Dulu waktu masih kuliah S1, saya dengan mudahnya bisa membuat grafik tersebut dengan bantuan Maple. Nah, berhubung saya sudah tidak menggunakan software tersebut, saya akan gunakan R untuk melukis fungsi-fungsi matematika itu. Saya akan gunakan library(ggplot2) untuk melukisnya.

Kenapa melukis? Karena ggplot2 itu seperti canvas yang siap diisi object apapun.

---

Fungsi Sederhana vs Fungsi Rumit

Saya pribadi membagi fungsi yang saya temui menjadi dua jenis:

1. Fungsi sederhana: Fungsi yang bisa dituliskan dengan mudah hubungan antara sumbu x dan sumbu y. Selain itu, tidak ada ambiguitas hasil fungsi yang ada. Secara mudah saya sebut satu nilai x hanya menghasilkan satu nilai y. Contohnya: persamaan polinomial seperti y = x², fungsi trigonometri seperti y = sin x, dan lainnya.
2. Fungsi rumit: Fungsi yang kalau dilihat dengan mata biasa sudah rumit penulisannya. hehe. Selain itu satu nilai x bisa menghasilkan dua nilai y. Lho kok bisa? Coba perhatikan fungsi lingkaran satuan sebagai berikut: x² + y² − 1 = 0.

Oleh sebab itu, saya membuat dua functions berbeda di R yang bisa untuk melukis kedua jenis fungsi tersebut.

---

Fungsi Sederhana

Cara kerja untuk melukis fungsi sederhana gampang. Kita hanya perlu input berupa:

1. Fungsi matematika.
2. Batas bawah sumbu x, misal dinotasikan sebagai a.
3. Batas atas sumbu x, misal dinotasikan sebagai b.

Langkahnya adalah:

• STEP 1 Membagi selang [a, b] dengan Δ sekecil mungkin (kita akan definisikan nilai deltanya).
• STEP 2 Menghitung nilai f(x), ∀x ∈ [a, b].
• STEP 3 Memplot datanya.

Beginilah function-nya:

gambar_fx = function(f,a,b,delta){
  temp = data.frame(
    x = seq(a,b,by = delta)
  ) %>% 
    mutate(y = f(x)) %>% 
    filter(!is.nan(y))
  subtitle = paste0("Pada selang [",a,",",b,"]")
  caption = "Digambar dengan R\nikanx101.com"
  temp %>% 
    ggplot(aes(x,y)) +
    geom_line(color = "steelblue") +
    theme_minimal() +
    labs(title = "Grafik f(x)",
         subtitle = subtitle,
         caption = caption)
   
}

Sekarang kita akan uji untuk y = x³ − 2^x + 5x² − 8, x ∈ [ − 8, 8], Δ = 0.5.

f = function(x){x^3 - 2^x + 5*x^2 - 8}
a = -8
b = 8
delta = 0.5
gambar_fx(f,a,b,delta)

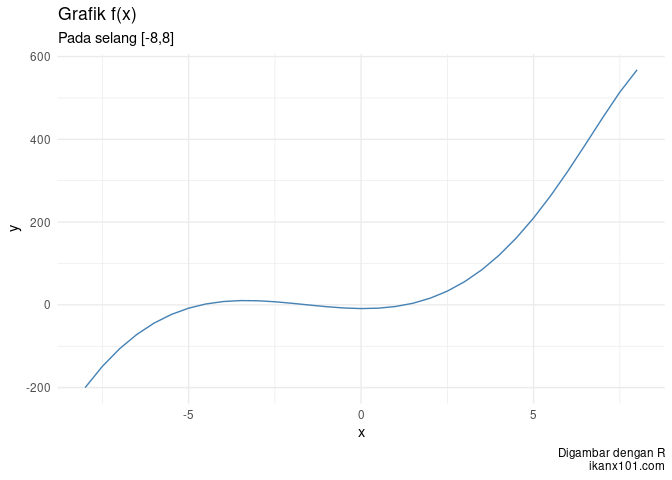
Kita uji kembali untuk fungsi trigonometri berikut: y = sin xcos x + sin 5^− x, x ∈ [ − π, π], Δ = 0.01.

f = function(x){sin(x) * cos(x) + sin(5^(-x))}
a = -pi
b = pi
delta = 0.01
gambar_fx(f,a,b,delta)

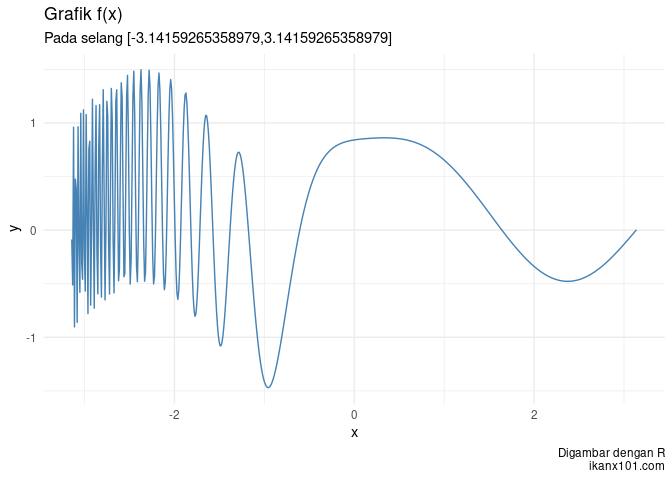
Kita uji kembali untuk fungsi logaritmik berikut: y = log x² + e^− 2x, x ∈ [0.1, 5], Δ = 0.01.

f = function(x){log(x^2) + exp(-2*x)}
a = 0.1
b = 5
delta = 0.01
gambar_fx(f,a,b,delta)

---

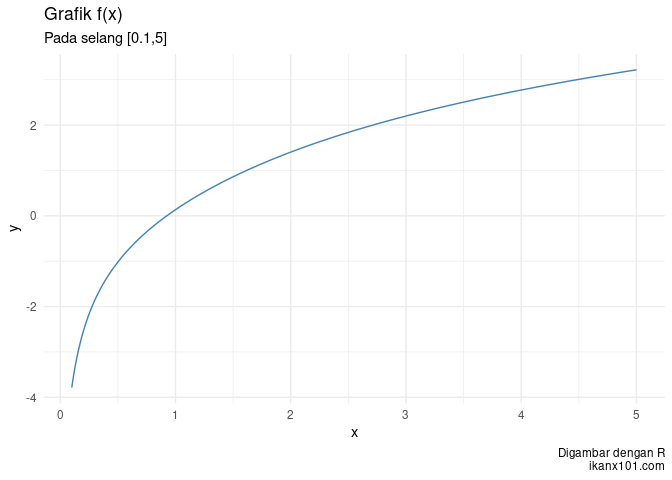
Fungsi Rumit

Sekarang saatnya kita membahas tentang melukis fungsi rumit. Bagi saya fungsi rumit adalah fungsi yang tidak bisa kita tuliskan secara eksplisit ke dalam bentuk y ∼ x. Contohnya adalah fungsi berikut: x² + y² − 10 = 0.

Jika kita paksakan agar menjadi bentuk y ∼ x, kita bisa kehilangan beberapa nilai penting.

Oleh karena itu, saya mengusulkan cara melukis sebagai berikut:

• STEP 1 Generate bagi-bagi selang [a, b] di sumbu x dan y dengan Δ kecil tertentu. Misalkan dinotasikan (x′, y′).
• STEP 2 Hitung nilai f(x′, y′).
• STEP 3 Kita hanya akan menampilkan (x′, y′) yang memenuhi f(x, y).

Berikut adalah function R-nya:

grafik_fxy = function(a,b,delta,f){
  selang = seq(a,b,by = delta)
  df = 
    expand.grid(selang,selang) %>% 
    as.data.frame() %>% 
    rename(x = Var1,
           y = Var2) %>%  
    mutate(f = f(x,y)) %>%
    filter(round(f,1) == 0) 
  df %>% 
    ggplot(aes(x,y)) +
    geom_point(color = "steelblue",
               size = .1) +
    labs(title = "Grafik f(x)",
         caption = "Digambar dengan R\nikanx101.com") +
    theme_minimal()
}

Kita akan uji untuk fungsi berikut: x² + y² − 10 = 0

f = function(x,y)x^2 + y^2 - 10
a = -11
b = 11
delta = 0.01
grafik_fxy(a,b,delta,f) + 
  coord_equal() # ditambah ini agar sb x dan sb y equal

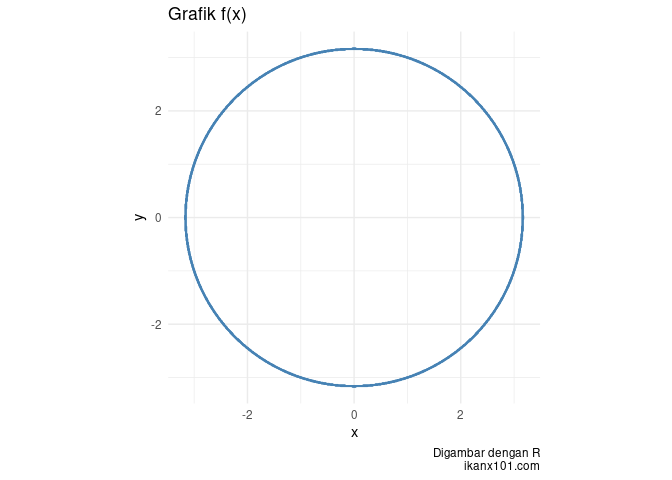
Kita uji kembali untuk fungsi berikut: (1/2) x y^2 + 2x - 5y + 8 = 0

f = function(x,y){(1/2)*x*y^2 + 2*x - 5*y + 8}
a = -11
b = 11
delta = 0.01
grafik_fxy(a,b,delta,f) 

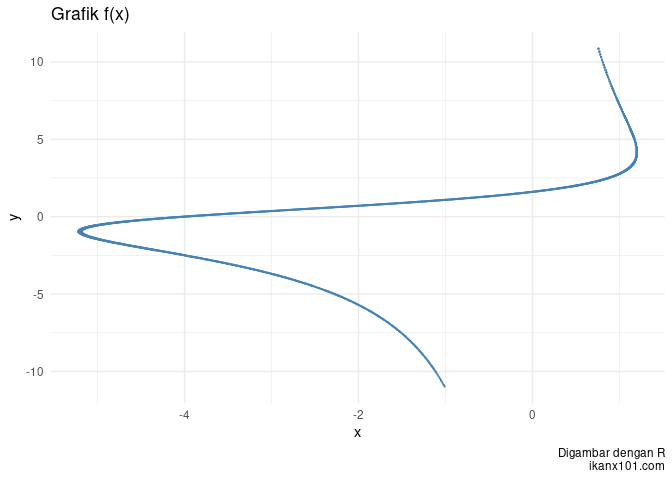
Gimana mudah kan?

---

if you find this article helpful, support this blog by clicking the ads.