Metode Numerik: Metode Bisection untuk Mencari Akar Persamaan

Hari ini adalah hari pertama saya kuliah S2 di Sains Komputasi ITB. Kuliah hari ini dibuka dengan mata kuliah Analisa Numerik Lanjut oleh Prof. Kuntjoro.

Ketika S1 dulu, saya pernah mengambil mata kuliah yang beliau ajar di Kelompok Keahlian Matematika Keuangan.

---

Nah, pada pertemuan pembuka ini dibahas materi refreshment saat kuliah Metode Numerik di S1 dulu yakni metode bisection untuk mencari akar dari suatu persamaan.

Mungkin banyak dari rekan-rekan sekalian yang bertanya-tanya:

Apa sih manfaat dari ilmu ini?

Numerik erat sekali kaitannya dengan aproksimasi. Percayalah bahwa menghitung dengan cara eksak biasanya lebih melelahkan dibandingkan dengan perhitungan numerik. Karena numerik sejatinya merupakan proses iterasi yang relatif mudah dilakukan.

---

Saya mulai dari definisi sederhana, apakah akar persamaan itu?

Akar dari persamaan adalah nilai saat fungsi kontinu bernilai nol.

Misalkan f(x) adalah fungsi kontinu. Setiap nilai r yang memenuhi f(r) = 0 disebut akar persamaan.

Kata kuncinya di sini adalah fungsinya harus kontinu yah.

Sekarang kita coba pikirkan baik-baik, jika saya memiliki fungsi f yang kontinu di selang [a, b] dengan f(a).f(b) < 0 artinya pasti ada suatu nilai c ∈ [a, b] sehingga f(c) = 0.

Pemikiran tersebut dilandasi oleh sebuah teorema bernama Intermediate Value Theorem (Teorema Nilai Antara).

Misalkan f ∈ C[a, b] dan L adalah suatu nilai di atara f(a) dan f(b). Maka ada suatu nilai c ∈ (a, b) yang memenuhi f(c) = L.

Atas dasar teorema ini metode bisection lahir. Bisection berarti membelah selang daerah fungsi menjadi dua dan mencari akar diantaranya. Begitu seterusnya hingga kita bisa “menerima” error atau galat yang dihasilkan.

Algoritma Metode Bisection

Berikut adalah algoritma atau langkah kerjanya:

• Step 1: Find a and b with a < b such that f(a).f(b) < 0.
• Step 2: Set c = (a + b)/2 and evaluate f(c). If f(c) = 0 then r = c and stop. Otherwise continue to Step 3.
• Step 3: If f(a).f(c) < 0 then reset b = c. Otherwise reset a = c.
• Step 4: If b–a < ϵ then stop. Use (a + b)/2 as the approximation to r. Otherwise return to Step 2.

Ilustrasi:

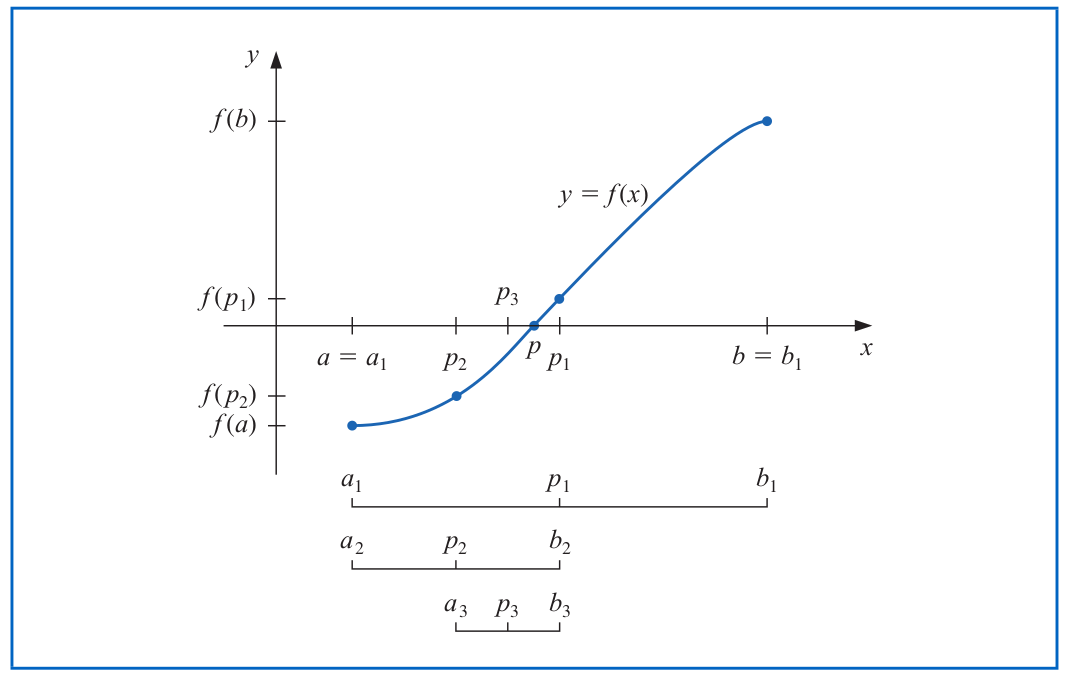
Ilustrasi Bisection

Untuk menemukan akar dari f(x), kita perlu set terlebih dahulu nilai a dab b yang dibutuhkan. Lalu kita ambil nilai tengah antara a dan b (misalkan p₁). Kita akan evaluasi nilai f(p₁). Kemudian kita akan bisection atau belah lagi menjadi p₂, p₃, dan seterusnya hingga diterima.

Kategori penerimaan bisa kita definisikan galat tertentu yang bisa kita terima.

---

Contoh

Cari nilai x di selang [0, 2] yang memenuhi persamaan x.sin(x) = 1.

Masalah di atas sama dengan mencari nilai x ∈ [0, 2] sehingga x.sin(x) − 1 = 0.

Perhatikan grafik fungsi berikut ini:

Terlihat bahwa:

1. f(x) kontinu pada selang tersebut.
2. Ada tepat satu titik c ∈ [0, 2] di mana nilai f(x) = 0.

Sekarang kita hitung berapa akar persamaannya menggunakan metode bisection di R sebagai berikut:

# clean global environment
rm(list=ls())

# informasi yang dibutuhkan
a = 0 # batas bawah
b = 2 # batas atas
f = function(x){x*sin(x)-1} # fungsi dari soal
iter_max = 50 # batas iterasi yang diperbolehkan
tol_max = 0.00000005 # galat atau error yang masih bisa saya terima

# initial condition
i = 1

# membuat rumah untuk hasil iterasi
hasil = data.frame(n = NA,
                   a = NA,
                   b = NA,
                   c = NA)

# iterasi dimulai dari sini
while(i <= iter_max && (b-a)/2 > tol_max){
  p = a + ((b-a)/2) # mengambil nilai p, yakni titik tengah antara a dan b
  FP = f(p) # hit f(p)
  FA = f(a) # hit f(a)
  FB = f(b) # hit f(b)
  hasil[i,] = list(i,a,b,p) # mencetak hasil perhitungan ke dalam "rumah" yang sudah disediakan
  if(FA*FP < 0){b = p} else{a = p} # ingat aturan bisection!
  i  = i + 1 # penambahan i pada iterasi
}

n	a	b	c
1	0.000000	2.000000	1.000000
2	1.000000	2.000000	1.500000
3	1.000000	1.500000	1.250000
4	1.000000	1.250000	1.125000
5	1.000000	1.125000	1.062500
6	1.062500	1.125000	1.093750
7	1.093750	1.125000	1.109375
8	1.109375	1.125000	1.117188
9	1.109375	1.117188	1.113281
10	1.113281	1.117188	1.115234
11	1.113281	1.115234	1.114258
12	1.113281	1.114258	1.113770
13	1.113770	1.114258	1.114014
14	1.114014	1.114258	1.114136
15	1.114136	1.114258	1.114197
16	1.114136	1.114197	1.114166
17	1.114136	1.114166	1.114151
18	1.114151	1.114166	1.114159
19	1.114151	1.114159	1.114155
20	1.114155	1.114159	1.114157
21	1.114157	1.114159	1.114158
22	1.114157	1.114158	1.114157
23	1.114157	1.114157	1.114157
24	1.114157	1.114157	1.114157
25	1.114157	1.114157	1.114157

Kita dapatkan nilai f(c) = 0 pada c= 1.1141571 dengan toleransi ϵ= 5^{-8} pada iterasi ke 25 kali

---

if you find this article helpful, support this blog by clicking the ads