Math and Computational Science for Business part 2: Validasi Hipotesis dalam Sales dan Distribusi
Kembali lagi dalam topik terbaru dalam blog saya. Kali ini melanjutkan tulisan sebelumnya (sudah baca kan ya? Jika belum, silakan dibaca dulu ya) saya akan membahas bagaimana matematika dan sains komputasi bisa digunakan untuk membantu dalam bisnis. Sama seperti pada tulisan sebelumnya, saya tidak ingin terjebak ke dalam teknis algoritma dan how to-nya. Saya ingin memberikan ide, konsep, dan prinsip yang bisa digunakan pada bisnis.
Pada tulisan ini, saya akan memberikan satu use case menarik di mana simulasi Monte Carlo bisa digunakan untuk memvalidasi sebuah hipotesis yang dimiliki oleh salah seorang sales manager di sebuah perusahaan FMCG terkemuka.
Bagaimana ceritanya? Cekidot!
Suatu hari saya bertemu dengan seorang sales manager dengan level legendary di suatu kota. Beliau sudah berkarir sejak lama (hanya beda beberapa tahun dari total umur saya saat ini). Beliau memberikan challenge kepada saya untuk bisa membuktikan teori yang dia kembangkan.
Sebagai seorang (yang mengaku scientist), mungkin akan lebih aman jika saya menuliskan kata teori sebagai hipotesis. Hehe
Bagaimana hipotesisnya? Beliau memberikan sebuah proposisi sebagai berikut:
Jika performa distribusi di atas 40%, maka distribution error akan berada di bawah 20%.
Untuk menjelaskan apa yang dimaksud dengan performa distribusi dan distribution error, perhatikan ilustrasi sebagai berikut:
Ilustrasi
Misalkan seorang sales manager di kota tertentu bertanggung jawab untuk memasarkan produk A. Dalam rentang waktu Januari hingga Agustus, beliau memiliki data transaksi berapa banyak dan siapa saja toko (atau outlet) yang membeli produk A dari perusahaannya sebagai berikut:

Semua toko yang telah bertransaksi sejak Januari hingga Agustus disebut dengan registered outlet (RO). Sedangkan toko yang aktif bertransaksi di suatu bulan tertentu disebut dengan active outlet (AO).
Performa distribusi adalah rata-rata rasio AO per RO selama bulan Januari hingga Agustus, atau bisa saya tuliskan sebagai:
Angka delapan artinya ada delapan bulan sejak Januari hingga Agustus (ingat rumus rata-rata yah).
Sedangkan distribution error adalah rasio dari berapa banyak RO yang tidak bertransaksi sama sekali di tiga bulan terakhir (Juni, Juli, dan Agustus) per total semua RO yang ada.
Dari definisi di atas dan dari ilustrasi tabel yang saya berikan, maka
besaran performa distribusi adalah rata-rata dari baris Rasio AO/RO
pada baris ke 15, yakni sebesar: 26.25%. Sedangkan besaran
distribution error dari kasus di atas adalah sebesar 20% (2 toko
dari 10 RO).
Pertanyaan pertama yang terbersit dalam pikiran saya adalah bagaimana caranya memvalidasi pernyataan sang legendary sales manager tersebut?
Jujurly, untuk mendapatkan data transaksi detail seperti yang ada dalam ilustrasi tersebut tampaknya sulit bagi saya. Sampai suatu saat saya berpikir:
Bagaimana jika di Monte Carlo-in saja!
Caranya adalah dengan membuat data transaksi sintetis selama tiga bulan berturut-turut dengan input berupa persentase performa distribusi yang beragam. Ingat kembali definisi dari performa distribusi!
Performa distribusi adalah rata-rata persentase rasio AO dengan RO. Dari definisi ini saja kita sudah bisa melihat bagaimana kira-kira bekerjanya simulasi tersebut.
Saya akan buat algoritmanya sebagai berikut dan melakukan simulasi
sebanyak
kali. Berikut adalah flowchart simulasinya.
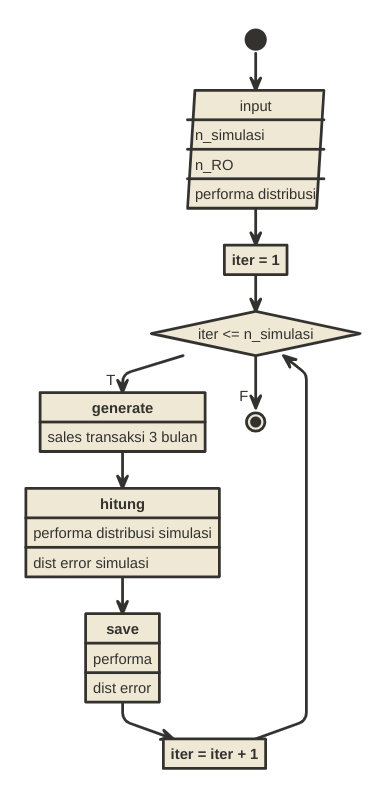
Bagaimana hasilnya? Berikut adalah grafik scatterplot antara performa distribusi dan distribution error:

Saya tambahkan pula dalam grafik tersebut garis biru yang merupakan formula smoothing dari titik data hasil simulasi.
Hal yang mengejutkan ternyata angka performa distribusi sebesar 40% memiliki nilai distribution error sekitar 20% berdasarkan model pada garis biru.
Ternyata memang benar experience matters pada kasus ini. Ucapan sang legendary sales manager benar adanya.
Pertanyaan selanjutnya adalah menentukan critical area bagi suatu produk. Maksudnya adalah kapan kita bisa menentukan suatu produk tidak sedang baik-baik saja dan perlu diberikan treatment khusus sebelum terlambat.
Cara termudah yang saya bisa lakukan adalah dengan menentukan area awal
di sumbu yang
memberikan kenaikan drastis pada sumbu
. Konsep ini di kalkulus
disebut dengan diferensial atau turunan.
Perhatikan kembali grafik persamaan garis dari hasil simulasi (grafik sebelumnya) berikut ini:

Dari grafik di atas, saya coba hitung nilai
secara numerik lalu saya buatkan grafiknya sebagai berikut:

Dugaan saya, grafik awal
dan grafik
merupakan fungsi eksponensial karena bentuk grafiknya hampir sama.
Nah, dari grafik
kita bisa lihat secara visual dari grid grafik bahwa pada area di
sebelah kiri garis merah memiliki turunan yang lebih curam dibanding
area di sebelah kanan garis merah.
Garis merah tersebut berada pada titik performa distribusi sebesar
.
Kesimpulan Sementara
Critical area yang bisa saya simpulkan secara sederhana adalah pada
saat produk memiliki performa distribusi di bawah
, maka produk
tersebut sudah harus mendapatkan treatment khusus sebelum
distribution error-nya menjadi lebih tinggi.
Remarks
Pada contoh di atas, sang legendary sales manager memberikan simplifikasi dimana sales value permasing-masing toko tidak dilihat pada aturan 40-20 miliknya. Namun besaran sales value kelak akan dilihat sebagai persentase kontribusi masing-masing toko terhadap sales total produknya.
Hal ini berguna saat ada produk dengan performa jelek, maka toko-toko yang tidak membeli produk sama sekali dalam tiga bulan akan dilihat siapa saja top contributors-nya. Special treatment akan dilakukan kepada toko-toko tersebut.
Pada penjelasan artikel ini, saya hanya membuat simulasi Monte Carlo untuk membandingkan performa distribusi dengan distribution error tanpa melihat sales value per masing-masing toko.
if you find this article helpful, support this blog by clicking the ads.
