Metode Numerik: Metode Newton untuk Mencari Akar Persamaan

Pada tulisan sebelumnya, saya sudah membahas bagaimana metode bisection digunakan untuk mencari akar suatu persamaan.

Walaupun metode tersebut powerful tapi kalau kita ingat kembali dibutuhkan dua titik awal iterasi (misal dan ) dengan syarat wajib: dan kontinu di selang .

dan harus berlawanan tanda. Salah satu harus positif dan lainnya negatif.

Kenapa harus begitu? Ingat kembali Teorema Nilai Antara yang saya sebutkan juga di tulisan tersebut yah.

Metode Newton

Metode bisection bukanlah satu-satunya metode numerik yang bisa digunakan untuk mencari akar persamaan. Salah satu metode lain yang terkenal adalah metode Newton.

Berbeda dengan bisection yang membutuhkan 2 buah titik awal iterasi, metode Newton cukup menggunakan satu titik saja.

Lho kok bisa?

Misalkan saya memiliki fungsi: dengan grafik sebagai berikut:

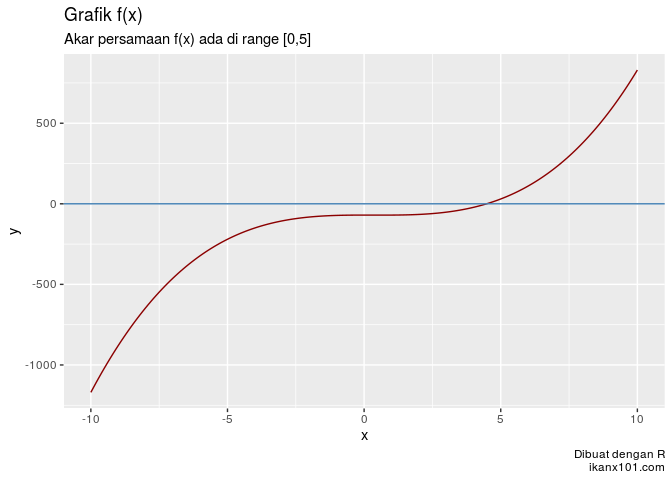
Untuk mencari akar persamaan dengan bisection, kita butuh selang sebagai permulaan iterasi.

Namun, dengan metode Newton kita bisa mengambil titik manapun dari grafik di atas sebagai titik permulaan.

---

Bagaimana cara kerjanya?

Metode Newton memanfaatkan Deret Taylor (Taylor Series) dari suatu fungsi. Kali ini syarat agar metode Newton bisa digunakan adalah fungsinya bisa diturunkan (diferensiable).

Misalkan dari suatu fungsi memiliki suatu akar . Saya ingin menghitung suatu barisan yang akan konvergen ke akar . Untuk suatu nilai yang sangat amat kecil:

Dengan:

1. Mengabaikan (karena si sudah kecil sehingga saat dikuadratkan juga akan lebih kecil lagi).
2. karena kita ingin mencari akar persamaan.

Maka kita bisa dapatkan:

Sehingga menghasilkan:

Ingat kembali bahwa kita ingin sangat dekat sekali dengan akar persamaan .

Sehingga:

Persamaan terakhir ini menjadi dasar bagi algoritma pengerjaan metode Newton.

Algoritma Newton

---

Contoh Pengerjaan

Sekarang kita akan gunakan metode Newton ini untuk menyelesaikan contoh soal sebelumnya:

Berikutnya kita perlu mencari turunan dari . Untuk melakukan itu, kita bisa melakukannya manual dengan mencoret-coret di kertas atau dengan bantuan library(Ryacas) yang pernah saya tulis sebelumnya. Sehingga didapatkan:

library(Ryacas)
eq = "x^3 - x^2 - 70"
eq %>% y_fn("D(x)") %>% yac_str()

## [1] "3*x^2-2*x"

Setelah itu, saya akan set titik awal iterasinya di (bebas yah mau berapa saja).

Sebagai penunjang algoritma yang saya buat, saya akan atur:

1. Iterasi maksimum yang dijalankan adalah 50.
2. Tingkat akurasi atau ketelitian hasil aproksimasinya adalah saja.

# informasi yang dibutuhkan
x_0 = 10
f = function(x){x^3 - x^2 - 70}
df = function(x){3*x^2-2*x}
iter_max = 50
tol_max = 10^-2

# initial condition
i = 1
hasil = data.frame(n_iter = 0,
                   p = x_0)

while(i <= iter_max){
  p = x_0 - (f(x_0) / df(x_0))
  hasil[i+1,] = list(i,p)
  if(abs(p-x_0) < tol_max){break}
  x_0 = p;
  i  = i + 1
}
# print output
hasil %>% knitr::kable(align = "c")

n_iter	p
0	10.000000
1	7.035714
2	5.333925
3	4.620209
4	4.487392
5	4.483027

Ternyata hanya dibutuhkan 5 kali iterasi untuk mendapatkan aproksimasi akar persamaannya.

Sekarang saya akan coba melakukan ulang tapi dengan titik awal .

# informasi yang dibutuhkan
x_0 = -7
f = function(x){x^3 - x^2 - 70}
df = function(x){3*x^2-2*x}
iter_max = 50
tol_max = 10^-2

# initial condition
i = 1
hasil = data.frame(n_iter = 0,
                   p = x_0)

while(i <= iter_max){
  p = x_0 - (f(x_0) / df(x_0))
  hasil[i+1,] = list(i,p)
  if(abs(p-x_0) < tol_max){break}
  x_0 = p;
  i  = i + 1
}
# print output
hasil %>% knitr::kable(align = "c")

n_iter	p
0	-7.000000
1	-4.130435
2	-1.480342
3	6.431152
4	5.040797
5	4.546821
6	4.483989
7	4.483022

Dengan nilai yang berbeda, didapatkan aproksimasi akar pada iterasi ke 7.

---

Saya pribadi lebih menyukai metode ini karena algoritmanya sangat mudah dibuat.

if you find this article helpful, support this blog by clicking the ads.