Menghitung Nilai Pi dengan Trapezoid (Aproksimasi Numerik)
Pada post yang lalu, saya pernah menuliskan bagaimana simulasi
MonteCarlo digunakan untuk
mengaproksimasi nilai
. Jika kamu
belum membacanya, saya sarankan untuk membacanya terlebih dahulu.
Pada tulisan tersebut, saya mencoba mengaproksimasi dengan cara seperti
melempar darts ke
lingkaran. Luas
lingkarannya adalah rasio banyaknya darts on target per total lemparan
darts yang saya lakukan.

Aproksimasi Cara Lain
Sebenarnya ada banyak cara untuk menghampiri nilai
, salah satunya
adalah dengan menghitung integral atau luas daerah di bawah kurva
lingkaran berjari-jari 1 satuan.
Oke, untuk memudahkan, saya akan buat
lingkaran
berikut ini:
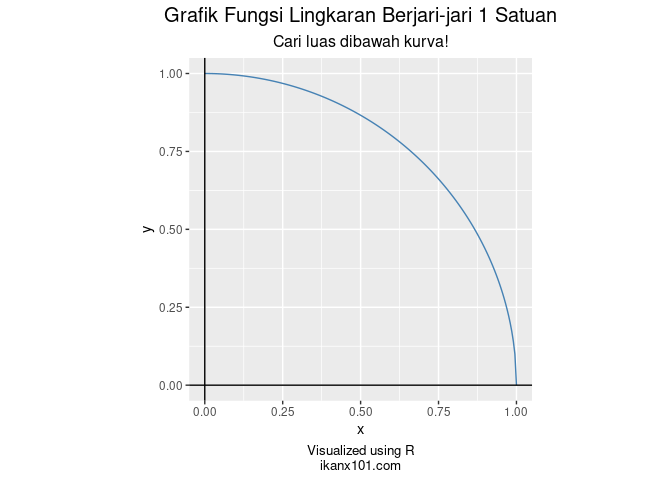
Ekspektasinya adalah:
.
Secara eksak, kita bisa menghitung integral fungsinya dan akhirnya
mendapatkan nilai
.
Bagaimana jika saya terlalu malas untuk melakukan integral?
Saya bisa memilih untuk melakukan pendekatan secara numerik. Yakni dengan menghitung luas di bawah kurva menggunakan hampiran trapezoid. Berikut adalah ilustrasinya:
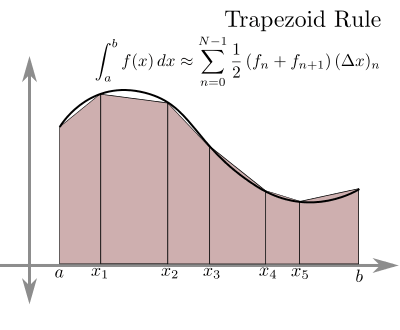
Sumber bragitoff.com
Menggunakan rumus yang tertera di atas, tugas kita sekarang “hanya” menentukan mau menggunakan nilai N berapa. N adalah berapa banyak trapezoid yang hendak kita generate. Tentunya semakin banyak, semaki akurat, tapi secara komputasi akan lebih “lama” (walaupun gak lama-lama banget donk).
Yuk kita hitung dengan berbagai macam nilai N. Kita akan bandingkan:
- Error-nya dengan nilai
default di R. Saya definisikan
.
- Processing time.
| N | Pi_hampiran | Error | Proc_Time |
|---|---|---|---|
| 5 | 3.037049 | 0.1045438 | 0.0016525 |
| 10 | 3.104518 | 0.0370743 | 0.0000131 |
| 40 | 3.136948 | 0.0046449 | 0.0000274 |
| 100 | 3.140417 | 0.0011756 | 0.0000610 |
| 400 | 3.141446 | 0.0001470 | 0.0002158 |
| 1000 | 3.141555 | 0.0000372 | 0.0005553 |
| 2500 | 3.141583 | 0.0000094 | 0.0013666 |
| 5000 | 3.141589 | 0.0000033 | 0.0026932 |
| 10000 | 3.141592 | 0.0000012 | 0.0052893 |
| 25000 | 3.141592 | 0.0000003 | 0.0155118 |
| 60000 | 3.141593 | 0.0000001 | 0.0341628 |
Terkonfirmasi yah bahwa semakin banyak N hasil hampirannya semakin akurat dan processing time-nya relatif lebih lama.
if you find this article helpful, support this blog by clicking the ads.
