Memahami Distribusi Poisson dari Peristiwa Saat Training Karyawan Baru

10 minute read

Dalam rentang setahun, biasanya Nutrifood mengadakan dua sampai tiga kali rekrutmen management trainee (kalau saya gak salah ingat ya). Sejak dulu, saya selalu mengisi satu session orientasi karyawan baru di setiap bacth management trainee. Biasanya di akhir session saya membuka ruang untuk rekan-rekan management trainee bertanya dan berdiskusi. Menurut ingatan saya, rata-rata ada 5 pertanyaan yang diajukan di setiap session.

Namun pada session di batch terakhir, saya mendapatkan 9 pertanyaan.

Lantas saya memberikan notes kepada tim HR bahwa batch terakhir ini spesial. Seingat saya, pernah beberapa bacthes yang “sepi” dari diskusi sama sekali.

Cerita saya di atas adalah contoh nyata suatu kejadian yang mengikuti distribusi Poisson. Distribusi Poisson adalah salah satu distribusi probabilitas diskrit yang digunakan untuk memodelkan sejumlah kejadian dalam suatu interval waktu atau area tertentu. Distribusi ini dinamai dengan nama matematikawan Prancis Siméon Denis Poisson (1781–1840).

Distribusi Poisson digunakan ketika:

Kejadian bersifat acak dan independen (terjadinya satu kejadian tidak memengaruhi kejadian berikutnya).
Rata-rata kejadian diketahui (λ) dan konstan dalam interval yang diamati.
Interval dapat berupa waktu, panjang, area, atau volume (misal: per jam, per km², per halaman buku).
Peluang lebih dari satu kejadian dalam interval sangat kecil (mendekati nol). Apa maksudnya?
- Interval sangat kecil bisa berupa:
  - Waktu yang sangat singkat (misal: detik, milidetik).
  - Ruang yang sangat sempit (misal: milimeter, area mikroskopis).
- Peluang >1 kejadian dalam interval kecil ≈ 0 berarti:
  - Hanya ada 0 atau 1 kejadian yang mungkin terjadi dalam waktu/ruang yang sangat sempit.
  - Contoh:
    - Dalam 1 milidetik, hampir tidak mungkin ada 2 panggilan telepon sekaligus di call center.
    - Dalam satu detik, hampir tak mungkin ada dua pasien yang datang bersamaan ke dokter.

Salah satu karakteristik utamanya adalah nilai mean sama dengan nilai variansinya. Keduanya diwakili oleh parameter tunggal, yaitu lambda (λ). Penjelasan intuitifnya adalah:

Kejadian Poisson Bersifat Acak & Independen
- Karena kejadian terjadi secara acak, tidak ada “kecenderungan” kejadian saling memengaruhi atau berkelompok.
- Contoh: Jika hari ini banyak email spam, spam di esok hari tidak dipengaruhi oleh hari ini.
Tidak Ada Faktor “Pengurangan” Peluang
- Pada distribusi Binomial, peluang sukses ( $p$ ) dan gagal ( $1-p$ ) mempengaruhi nilai variansi ( $\sigma^2 = np(1-p)$ ).
- Pada distribusi Poisson, tidak ada ( $1-p$ ) karena kejadian bisa terjadi berapa pun (tidak seperti Binomial yang terbatas $n$ percobaan).
Laju Kejadian () Konstan
- Karena $\lambda$ tetap, sebaran data mengikuti laju ini tanpa faktor tambahan yang mengubah penyebarannya.

Analogi

Analogi I

Bayangkan kita menjatuhkan banyak biji jagung ke suatu lantai:

Misalkan rata-rata ( $\mu$ ) sebesar 5 biji per meter persegi ( $\lambda = 5$ ).
Karena biji jatuh secara acak dan tidak saling memengaruhi, sebarannya mengikuti rata-rata ( $\sigma^2 = 5$ ).
Jika variansi > mean: Berarti biji cenderung berkelompok (tidak acak).
Jika variansi < mean: Berarti biji terlalu teratur (jarang berdekatan).

Poisson selalu acak, jadi $\mu = \sigma^2$ .

Analogi II

Misalkan rata-rata kecelakan lalu lintas dua kali per minggu ( $\lambda = 2$ ). Apa artinya?

Jika $\sigma^2 > \lambda$ (misalkan: $\sigma^2 = 4$ ), artinya kecelakaan cenderung berkelompok (misal: hari hujan banyak kecelakaan, hari cerah sedikit).
Jika $\sigma^2 < \lambda$ (misalkan: $\sigma^2 = 1$ ), artinya kecelakaan terlalu teratur (misal: ada pengaturan lalu lintas yang mengurangi variasi).

Rumus distribusi Poisson:

Peluang terjadinya $k$ kejadian dalam interval tertentu dituliskan sebagai berikut:

$P(X=k) = \frac{e^{-\lambda}.\lambda^k}{k!}$

di mana:

$P(X=k)$ menandakan peluang terjadinya $k$ kejadian.
$\lambda$ menandakan mean kejadian per interval.
$e$ merupakan bilangan Euler.
$k!$ merupakan $k$ faktorial. Misalkan: $4! = 4 \times 3 \times 2 \times 1 = 24$

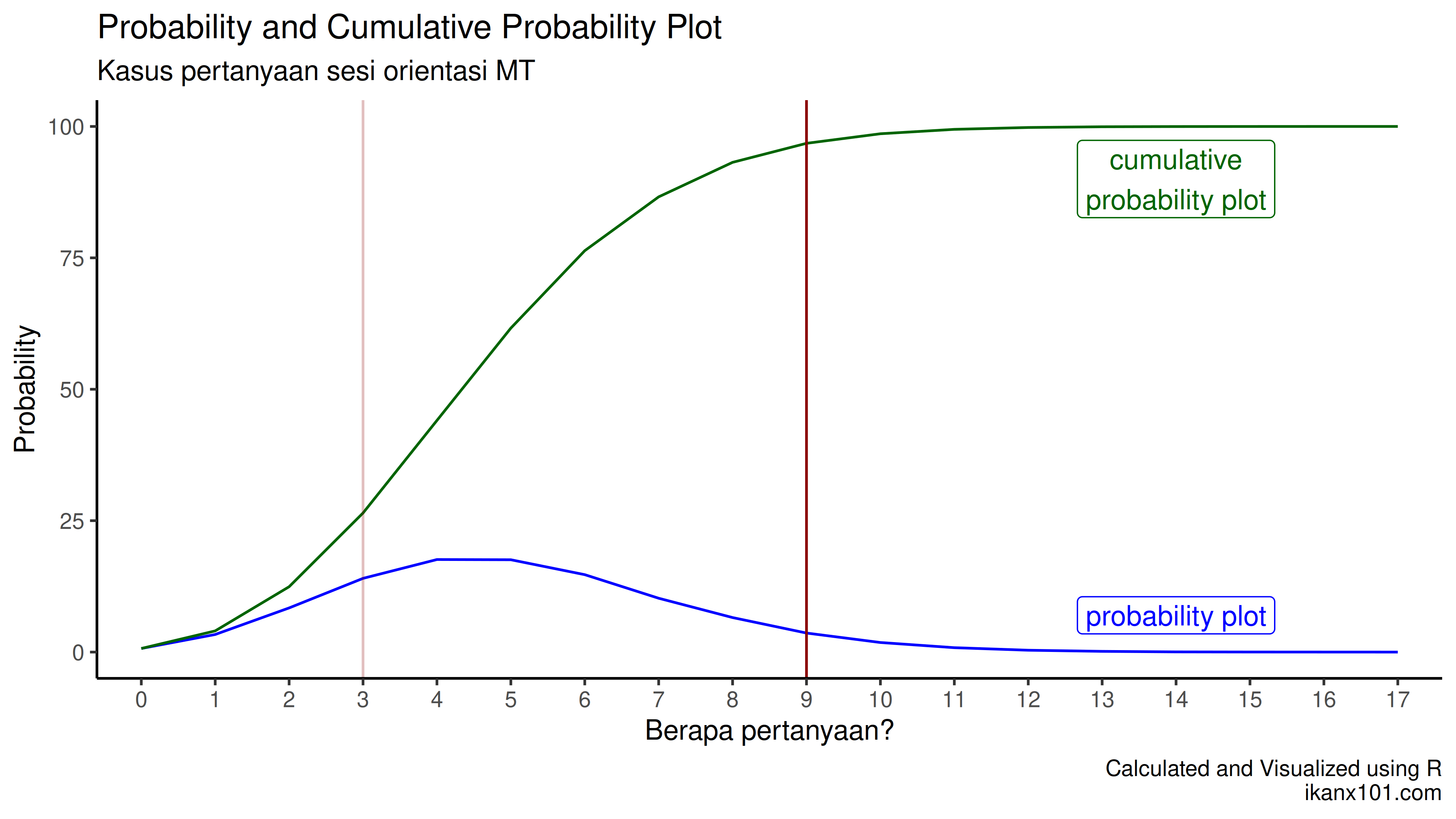
Dari rumus di atas dan dari kasus management trainee Nutrifood, saya bisa menghitung berapa peluang saya mendapat 9 pertanyaan pada session orientasi karyawan. Begini hasilnya:

Peluang terjadinya sesi diskusi yang “ramai”:
1. Peluang terjadi persis 9 pertanyaan dalam session: $P(X = 9) = 3.63\$
2. Peluang terjadi 9 pertanyaan atau lebih dalam session: $P(X \geq 9) = 3.18\$
Peluang terjadinya sesi diskusi yang “sepi”:
1. Peluang terjadi persis 3 pertanyaan dalam session: $P(X = 3) = 14.04\$
2. Peluang terjadi 3 pertanyaan atau kurang dalam session: $P(X \leq 3) = 26.5\$

Dari perhitungan di atas, ternyata memang peluang terjadinya batch yang “sepi” memang jauh lebih besar dibandingkan dengan batch yang “ramai”.

Berikut adalah grafik probability-nya:

Kapan Distribusi Poisson Tidak Berlaku?

Jika kejadian tidak independen (misal: gempa susulan setelah gempa utama).
Jika λ berubah-ubah dalam interval yang diamati.
Jika peluang kejadian tidak kecil (lebih baik pakai Binomial atau distribusi lain).

if you find this article helpful, support this blog by clicking the ads.

Appendix

Hubungan Distribusi Poisson dengan Distribusi Normal

Distribusi Poisson dapat menjadi pendekatan untuk Binomial jika:

$n$ (jumlah percobaan) sangat besar,
$p$ (peluang sukses) sangat kecil,
$\lambda = n . p$ (konstan).

Contoh:

Kasus kecelakaan lalu lintas: Peluang kecelakaan per mobil sangat kecil, tetapi jumlah mobil sangat besar.
Kasus cacat produksi: Peluang suatu produk cacat sangat kecil, tetapi jumlah produksi sangat besar.

Siapa Prancis Siméon Denis Poisson?

Siméon Denis Poisson (1781–1840) adalah matematikawan dan fisikawan Prancis yang terkenal berkat kontribusinya dalam teori probabilitas dan fisika matematika. Lahir di Pithiviers, Prancis, Poisson belajar di École Polytechnique di Paris di bawah bimbingan ilmuwan ternama seperti Pierre-Simon Laplace dan Joseph-Louis Lagrange. Karyanya mencakup berbagai bidang, termasuk statistik, astronomi, dan elastisitas material.

Salah satu kontribusi terbesarnya adalah Distribusi Poisson, sebuah model probabilitas untuk peristiwa langka yang kini banyak digunakan dalam analisis antrian, kedokteran, dan teknik. Selain itu, namanya juga diabadikan dalam Persamaan Poisson (dalam fisika matematika) dan Rasio Poisson (dalam teori elastisitas). Meski awalnya bercita-cita menjadi dokter, kegagalannya dalam ujian kedokteran justru membawanya menjadi salah satu matematikawan terpenting abad ke-19.

Poisson dikenal sebagai ilmuwan yang produktif namun sering terlibat persaingan sengit dengan sesama matematikawan, seperti Augustin-Louis Cauchy. Meski kurang terkenal dibanding Gauss atau Laplace, warisannya tetap hidup melalui konsep-konsep matematika yang digunakan hingga hari ini, seperti pemodelan kecelakaan lalu lintas, peluruhan radioaktif, dan analisis sistem telekomunikasi.

Share on

X Facebook LinkedIn Bluesky

Bunch of Ideas, a little bit of Maths.

Memahami Distribusi Poisson dari Peristiwa Saat Training Karyawan Baru