Mencari Akar Polinomial dengan R

Beberapa waktu yang lalu, saya pernah membahas bagaimana cara mencari akar suatu fungsi dengan metode bisection, Newton, dan Golden Section Search. Ketiga metode ini sangat powerful untuk mencari akar suatu persamaan. Baik berupa fungsi polinom dan fungsi non polinom (trigonometri, logaritmik, dan lainnya).

Masalah baru muncul kalau ternyata akar dari fungsi tersebut adalah bilangan imajiner. Bagaimana cara menemukan akarnya?

---

Pada perkuliahan yang lalu, kami membahas tentang penggunaan numpy di Python untuk mencari akar dari fungsi polinom. Setelah saya cek, di base R (tanpa harus install library lainnya), ada fungsi sejenis bernama polyroot().

Saya belum melihat secara detail bagaimana cara menghitungnya, tapi percayalah R itu bukan dibuat secara serampangan. hehe. Kalau kita mengeksekusi perintah berikut di R: help("polyroot"). Kita bisa melihat penjelasan beserta referensi ilmiah dibalik algoritmanya.

Source
C translation by Ross Ihaka of Fortran code in the reference, with modifications by the R Core Team.

References
Jenkins, M. A. and Traub, J. F. (1972). Algorithm 419: zeros of a complex polynomial. Communications of the ACM, 15(2), 97–99. doi: 10.1145/361254.361262.

Ross Ihaka adalah seorang profesor, statistician, dan salah satu creator dari R.

Misalkan kita memiliki polinom dengan bentuk seperti berikut:

p(x) = z₁ + z₂x + z₃x² + .. + z_nx^n − 1

Cara menyelesaikan dengan R adalah dengan membuat vector berisi (z₁, z₂, z₃, …, z_n).

Mudah kan?

---

Contoh Soal I

Misalkan saya memiliki fungsi berikut:

y = x⁴ + 4x² + 7

Jika saya gambarkan pada selang [ − 5, 5], maka:

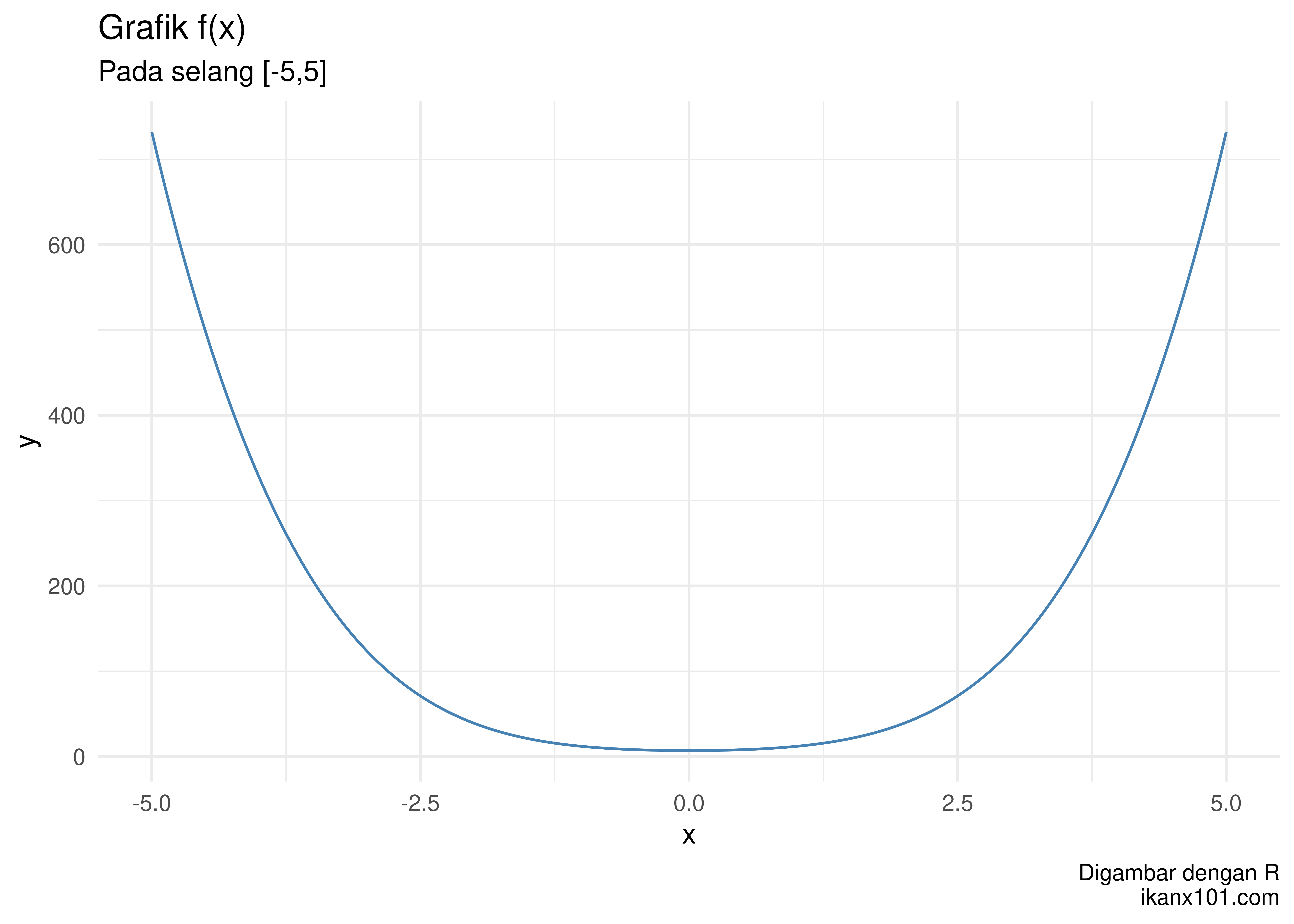
Terlihat bahwa f(x) tidak memiliki akar real. Kenapa? Secara visual tidak ada grafik f(x) yang memotong sumbu x.

Cara menghitungnya di R adalah sebagai berikut:

fungsi = c(7,0,4,0,1)
polyroot(fungsi)

## [1]  0.568221+1.524098i -0.568221+1.524098i -0.568221-1.524098i
## [4]  0.568221-1.524098i

Terlihat ada 4 akar bilangan imajiner dari f(x).

---

Contoh Soal II

Misalkan saya memiliki fungsi berikut:

y = 3x⁵ + 6

Jika saya gambarkan pada selang [ − 5, 5], maka:

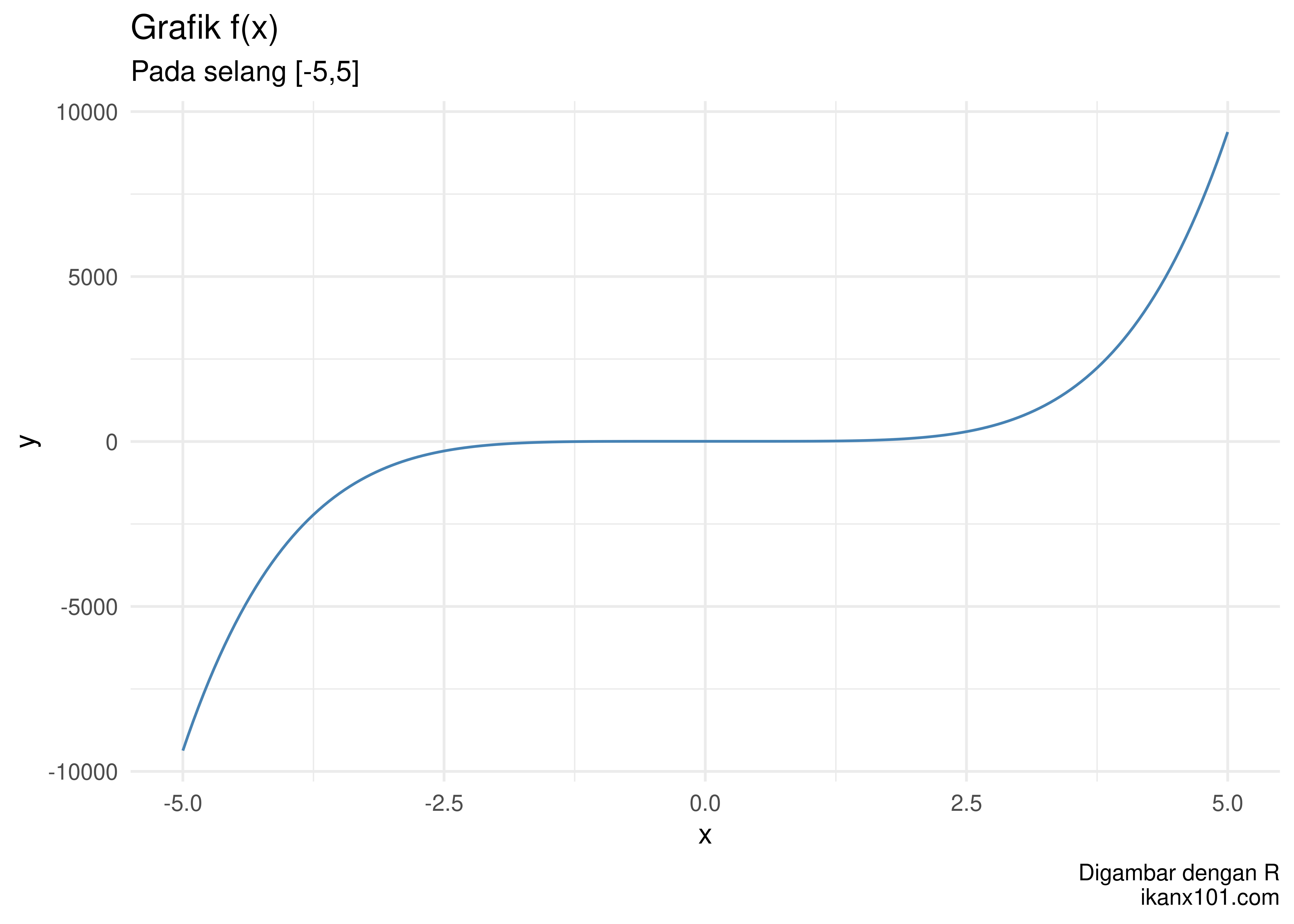
Terlihat bahwa f(x) memotong sumbu x. Artinya setidaknya ada satu akar bilangan real dari f(x).

Jika kita selesaikan dengan R menjadi:

fungsi = c(6,0,0,0,0,3)
polyroot(fungsi)

## [1]  0.9293165+0.675188i -0.3549673+1.092477i -0.3549673-1.092477i
## [4]  0.9293165-0.675188i -1.1486984+0.000000i

---

Contoh Soal III

Misalkan saya memiliki fungsi berikut:

y = 2x⁶ − 1.5x⁵ + 5x⁴ − 6.5x³ + 6x² − 3x + 4.5

Jika saya gambarkan pada selang [ − 5, 5], maka:

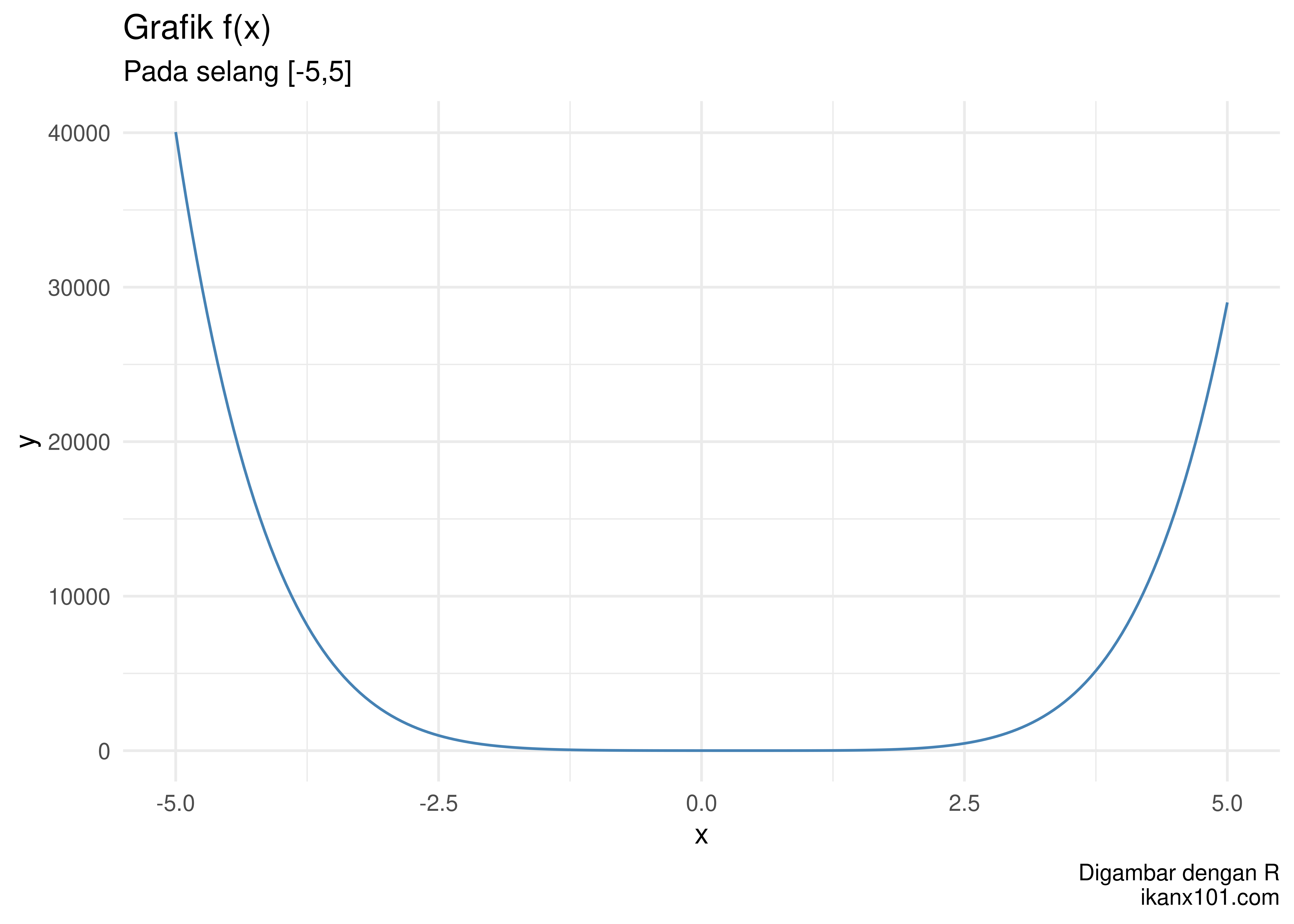
Secara grafik, kita tidak bisa melihat dengan jelas apakah ada perpotongan antara f(x) dengan sumbu x. Jadi kita selesaikan saja dengan R berikut:

fungsi = c(4.5,-3,6,-6.5,5,-1.5,2)
polyroot(fungsi)

## [1]  0.9270779+0.6020250i -0.2370896+0.8872501i -0.2370896-0.8872501i
## [4]  0.9270779-0.6020250i -0.3149883+1.4436086i -0.3149883-1.4436086i

---

if you find this article helpful, support this blog by clicking the ads.