Bagaimana Caranya Membandingkan Algoritma? Studi Kasus Bilangan Prima
Bagi saya, algoritma adalah sekumpulan baris perintah atau langkah kerja terstruktur yang berfungsi untuk melakukan komputasi.
Masing-masing orang memiliki gaya, cara, dan preferensinya sendiri dalam membuat algoritma.
Bisa jadi suatu permasalahan bisa diselesaikan dengan berbagai macam cara (algoritma). Lantas jika beberapa algoritma hasilnya sama-sama benar, bagaimana menentukan algoritma yang terbaik?
Kita bisa membandingkan seberapa cepat algoritma tersebut bekerja.
Istilahnya adalah computing time atau running time.
Saya akan bercerita tentang pengalaman saya dulu ketika kuliah.
Bilangan prima adalah bilangan yang hanya habis dibagi oleh dirinya sendiri.
Pada 2005 silam, saat saya sedang kuliah di tingkat dua, saya mengikuti salah satu mata kuliah wajib di Matematika. Nama mata kuliahnya adalah Komputasi Matematika. Mata kuliah ini adalah mata kuliah matematika dengan praktikum pertama kali.
Di tingkat pertama (alias TPB – Tahap Persiapan Bersama) hanya ada praktikum Fisika dan Kimia.
Saya ingat benar di laboratorium komputer, kami ditugaskan untuk membuat
program yang bisa mendeteksi apakah suatu bilangan termasuk bilangan
prima atau bukan. Waktu itu, bahasa yang digunakan adalah
Pascal.
Output-nya berupa executable file (.exe).
Waktu itu, proses yang saya lakukan adalah sebagai berikut:

Rekan sebelah saya, Anwar memberikan komentar:
“Kenapa harus ada looping dari 2 sampai n ?”
Sambil cengengesan saya menjawab:
“Ini adalah solusi yang menjamin suatu angka benar prima atau tidak…”
Saya yakin jawaban saya benar adanya tapi secara komputasi akan memakan waktu yang lama saat bilangan yang dimasukkan sangat besar. Waktu itu Anwar memberikan saran:
“Bagaimana jika kita bagi dua saja selang pencariannya? Alih-alih looping dari 2 hinnga n, kita akan looping dari 2 hingga $\frac{n}{2}$ saja.”
Bagaimana jika n yang dimasukkan adalah bilangan ganjil? Kita akan bulatkan $\frac{n}{2}$ ke atas. Lantas bagaimana dengan kriteria penentuannya?
Jika sebelumnya saya menggunakan kriteria count > 1 sebagai penentu bilangan tersebut bukan prima. Kali ini saya menggunakan kriteria count > 0 sebagai penentu.
Kenapa?
Karena looping-nya tidak sampai n. Jadi tidak ada kesempatan bagi bilangan prima bisa dibagi oleh dirinya sendiri.
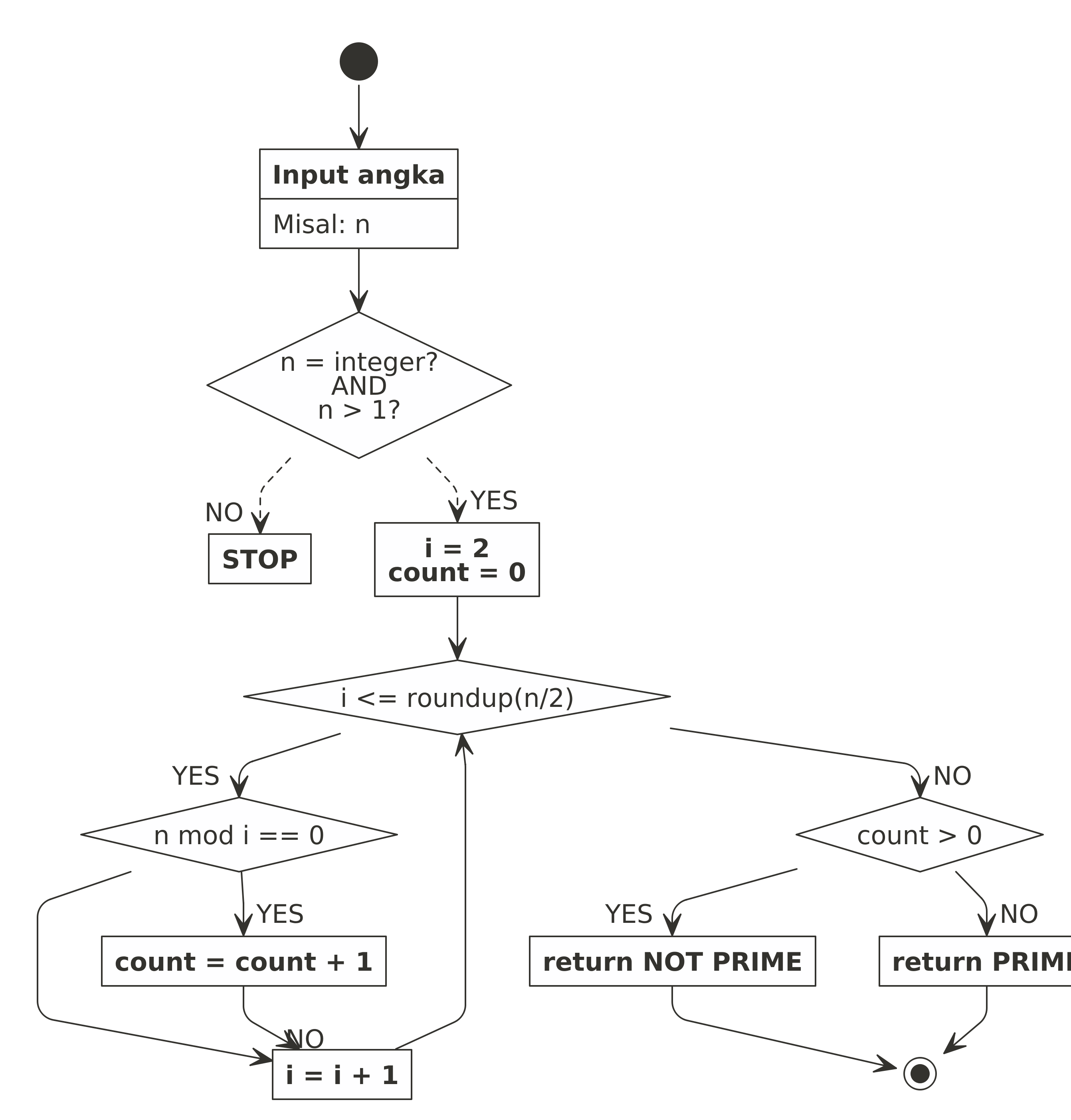
Setelah dimodifikasi tersebut, apakah ada perbedaan waktu komputasinya?
Saya telah membuat dua fungsi di R berdasarkan dua flowchart di atas. Mari kita bandingkan waktunya untuk mengecek suatu bilangan yang besar berikut:
is_prime(4092021)
## $kesimpulan
## [1] "Not Prime"
##
## $`waktu proses`
## Time difference of 6.544936 secs
is_prime_2(4092021)
## $kesimpulan
## [1] "Not Prime"
##
## $`waktu proses`
## Time difference of 3.227916 secs
Terlihat bahwa waktu komputasi pada function kedua lebih hemat ∼ 50% dari function pertama.
Lantas apakah ada cara penyelesaian (baca: algoritma) lain yang lebih cepat?
Kita bisa modifikasi flowchart kedua dengan cara:
Saat suatu bilangan berhasil dibagi oleh angka selain dirinya, kita akan stop iterasinya!
Saya menduga ini akan menjadi penghematan yang cukup besar mengingat kita tidak perlu melakukan looping terlalu banyak.

Sekarang kita cek waktu komputasinya dengan angka yang sama:
is_prime_3(4092021)
## $kesimpulan
## [1] "NOT PRIME"
##
## $`waktu proses`
## Time difference of 0.00001168251 secs
Jauh berkurang kan!
Mari kita coba kembali untuk angka lainnya.
is_prime(9988771)
## $kesimpulan
## [1] "Not Prime"
##
## $`waktu proses`
## Time difference of 15.50772 secs
is_prime_2(9988771)
## $kesimpulan
## [1] "Not Prime"
##
## $`waktu proses`
## Time difference of 7.801074 secs
is_prime_3(9988771)
## $kesimpulan
## [1] "NOT PRIME"
##
## $`waktu proses`
## Time difference of 0.000041008 secs
Algoritma ketiga cenderung akan sangat singkat karena biasanya hampir semua angka bisa dibagi oleh angka lain yang memiliki digit kecil.
Apakah ada cara lain? Tentu saja karena setiap orang pasti punya cara pikir yang berbeda-beda!
if you find this article helpful, support this blog by clicking the ads.
