Membedah Perhitungan Sample Size dari RAOSOFT

Sejak tahun 2012, saya terbiasa menggunakan sample size calculator online dari situs Raosoft untuk menghitung berapa banyak sampel responden yang saya harus cari untuk setiap project survey market riset. Situs ini merupakan layanan online gratis dengan input berupa empat parameter statistik tertentu.

Ada empat parameter yang harus dimasukkan agar kita bisa mendapatkan berapa banyak recommended sample dari situs tersebut, yakni:

• Margin of Error (tingkat presisi, biasanya 5% atau 3%) adalah batas maksimal perbedaan yang dapat diterima antara hasil sampel dan nilai sebenarnya di populasi. Misalnya, MoE 5% berarti hasil survei bisa berbeda ±5% dari kondisi aktual. Semakin kecil MoE, semakin presisi hasilnya, tetapi membutuhkan sampel lebih besar. MoE umumnya ditetapkan antara 1-10%, tergantung kebutuhan penelitian.
• Confidence Level (tingkat kepercayaan, misal 90%, 95%, atau 99%) menunjukkan seberapa yakin kita bahwa hasil survei berada dalam rentang Margin of Error. Misalnya, Confidence Level 95% berarti jika survei diulang 100 kali, 95 hasilnya akan berada dalam MoE yang ditentukan. Tingkat kepercayaan umumnya 90%, 95%, atau 99%, di mana semakin tinggi nilainya, semakin besar sampel yang dibutuhkan.
• Populasi Total (opsional, jika diketahui) adalah jumlah keseluruhan individu atau unit yang menjadi target penelitian. Jika populasi kecil (misal <1000), koreksi populasi terbatas diperlukan untuk menghindari oversampling. Namun, jika populasi sangat besar (misal >100.000), pengaruhnya terhadap ukuran sampel menjadi minimal.
• Response Distribution (perkiraan proporsi, default 50% untuk estimasi konservatif) adalah perkiraan proporsi populasi yang memiliki karakteristik tertentu. Nilai default 50% (0.5) digunakan karena menghasilkan ukuran sampel maksimal (paling konservatif). Jika proporsi sebenarnya diketahui (misal 70% setuju), menggunakan nilai tersebut bisa mengurangi kebutuhan sampel.

Perlu saya ingatkan sekali lagi bahwa jumlah MoE dan Confidence Level tidak harus 100%.

Contoh Cara Membaca Hasil Perhitungan Sampel:

Misalkan kita menggunakan kalkulator Raosoft dengan input berikut:

• Populasi Total (N) = 10.000 orang
• Margin of Error (MoE) = 5%
• Confidence Level = 95%
• Response Distribution = 50% (default)

Hasil Output: “Recommended sample size: 370”

Cara Membaca:

“Dengan populasi 10.000 orang, jika kita ingin survei memiliki tingkat akurasi ±5% (misalnya, jika 60% responden setuju, hasil sebenarnya di populasi diperkirakan antara 55-65%) dan tingkat kepercayaan 95% (artinya ada 95% kemungkinan hasil survei benar-benar mencerminkan populasi), maka sampel minimal yang diperlukan adalah 370 orang. Penggunaan proporsi 50% (response distribution) dipilih karena memberikan perhitungan sampel paling aman (terbesar) jika karakteristik populasi belum diketahui.”

---

Formula yang digunakan adalah formula Cochran untuk populasi tak terbatas (atau undefined) dan koreksi populasi terbatas (finite population correction) jika populasi dimasukkan.

Berikut ini adalah formula untuk populasi tak terbatas:

Di mana:

• = z-score (tergantung input confidence level),
• = proporsi estimasi (default 0.5),
• = margin of error.

Sedangkan berikut adalah koreksi jika populasi dimasukkan:

Misalkan:

• Confidence Level = 95% → z-score = 1.96
• Margin of Error = 5% → ()
• Populasi = 10.000
• Hasil: 370 sampel (tanpa koreksi populasi: 385).

Tapi perlu saya informasikan bahwa perhitungan sampel pada situs ini tidak diperuntukkan untuk desain riset yang kompleks.

Alternatif Skrip di R

Seperti biasa, kita bisa mereplikasi situs tersebut dengan membuat function di R sebagai berikut:

hitung_sampel <- function(N = NULL, e = 0.05, CL = 0.95, p = 0.5) {
  z <- qnorm(1 - (1 - CL)/2)
  n0 <- (z^2 * p * (1 - p)) / e^2
  if (!is.null(N)) n0 <- n0 / (1 + (n0 - 1)/N)
  ceiling(n0)
}

Berikut adalah contohnya:

# Contoh:
# populasi tak terbatas / undefined
hitung_sampel(e = 0.05, CL = 0.95)

[1] 385

# known populasi
hitung_sampel(N = 10000, e = 0.05, CL = 0.95)

[1] 370

Hubungan Populasi dengan Sample Size

Secara intuitif kita bisa menduga bahwa setiap penambahan populasi akan menambah sample size pula. Namun, semakin banyak populasi tak akan menambah sample size dengan signifikan. Kenapa? karena dari formula pertama, tidak berhubungan dengan . Akibatnya semakin besar pasti nilainya akan sama menjadi .

Untuk menggambarkan hal itu saya akan coba membuat grafik berikut ini:

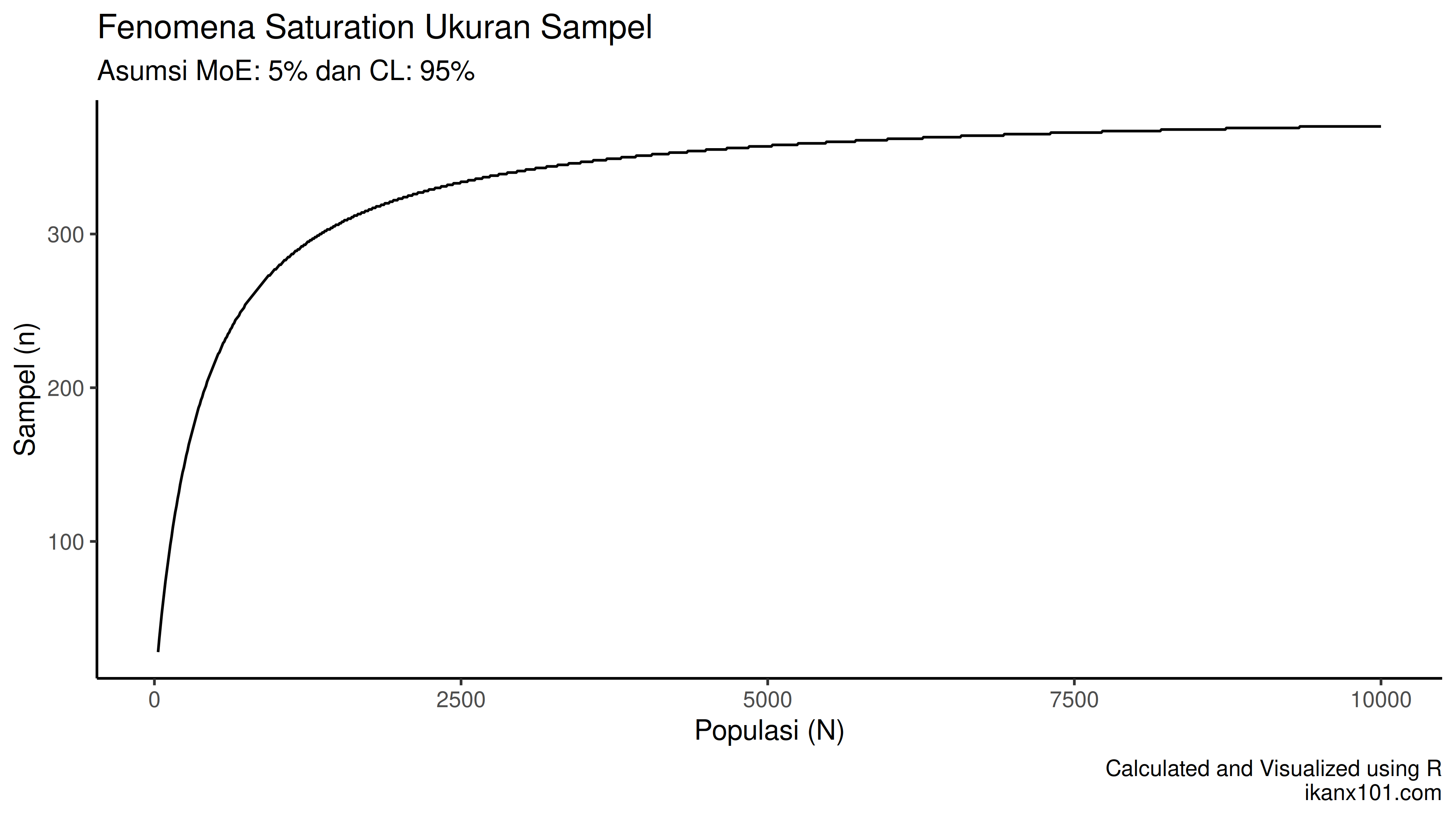
Dari grafik di atas, terlihat bahwa kurva menjadi saturated setelah populasi membesar. Penambahan populasi hanya berpengaruh signifikan jika kecil. Begitu melewati batas tertentu, ukuran sampel akan stabil mendekati . Ini memungkinkan survey berskala besar tetap efisien tanpa perlu sampel yang terlalu besar!

Implikasinya buat market researcher adalah:

1. Survei Nasional vs Lokal: survei di kota (populasi 1 juta) vs negara (300 juta) bisa menggunakan sampel yang hampir sama (±5% beda).
2. Efisiensi biaya: tidak perlu membesar-besarkan sampel hanya karena populasinya besar. Kesalahan umum: “Populasi 1 juta butuh sampel 10.000” → Tidak benar!

---

if you find this article helpful, support this blog by clicking the ads.