Bunch of Ideas, a little bit of Maths.

I am mathematician doing market research and data science

15 minute read

Pendahuluan

Pada pertengahan Juli 2025 ini, saya berkesempatan mengikuti event Industrial Mathematics Week 2025 (IMW 2025) di program studi Matematika ITB. Event ini berlangsung selama 5 hari di mana 2 hari pertama diisi dengan seminar dan 3 hari sisanya diisi dengan workshop menyelesaikan masalah real. Topik IMW pada tahun ini menitikberatkan pada optimisasi, vector-borne desease, dan deep learning.

Ada tiga masalah yang bisa dipilih untuk dikerjakan secara berkelompok selama workshop, yakni:

  1. Optimisasi portofolio saham,
  2. Penanganan penyebaran penyakit vector-borne, dan
  3. Optimisasi antrian lane security checking di bandara.

Saya pribadi memilih problem ketiga karena lebih dekat dengan pekerjaan saya sehari-hari. Singkat cerita, kelompok saya lebih memilih mengerjakan dengan metode deep learning tapi saya coba membuat satu model lain menggunakan linear programming sederhana.

Model ini sempat saya presentasikan di hari terakhir IMW dan mendapatkan sambutan baik dari si empunya problem sehingga diskusi berlangsung setelah event berakhir secara online.

Begini masalahnya:

Masalah

Di suatu bandara, setiap kali passengers hendak masuk ke waiting lounge, mereka harus melewati security checking. Petugas security terbatas sehingga lane yang tersedia hanya ada 17 lanes saja. Masing-masing security memiliki service rate tertentu.

Service rate didefinisikan sebagai berapa banyak passengers yang bisa diproses oleh seorang petugas security selama rentang waktu tertentu.

Perhatikan ilustrasi ini:

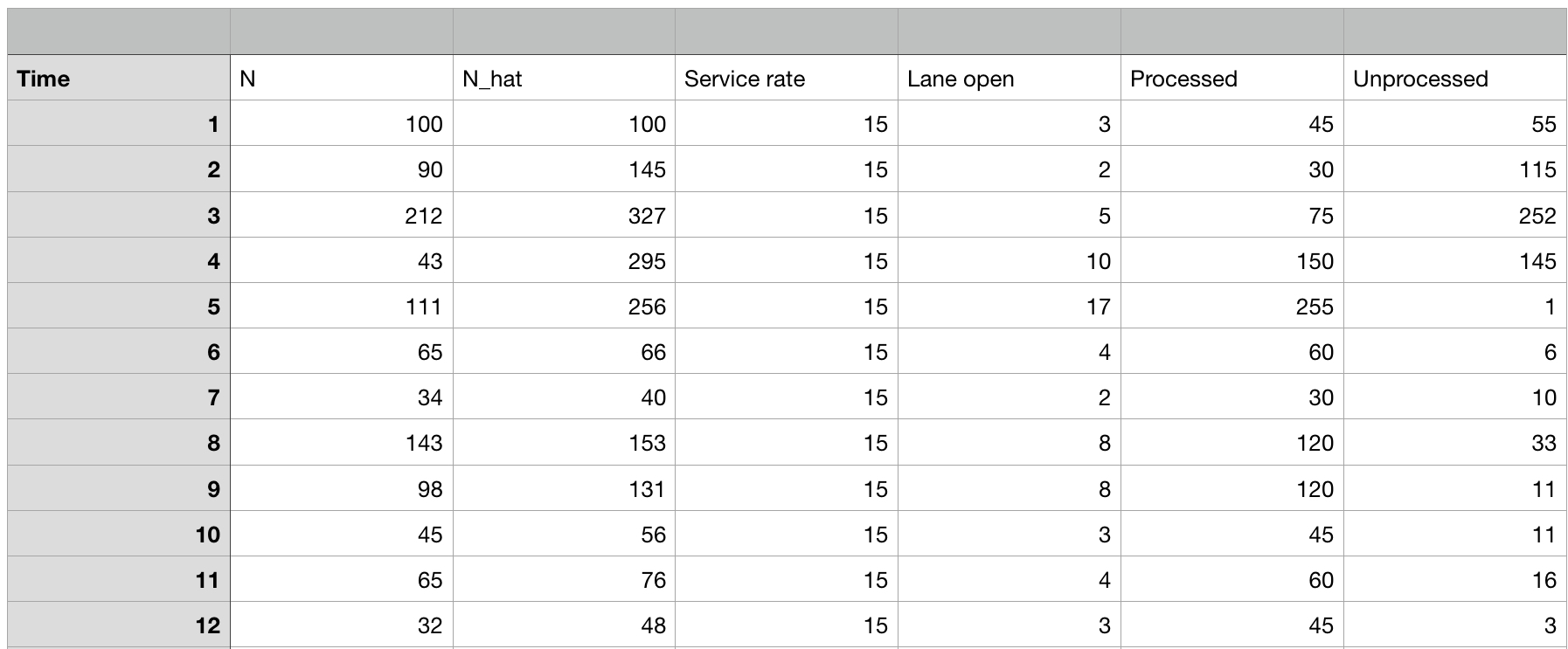
Setiap baris menandakan rentang waktu per 5 menit.

Pada rentang waktu 1, ada 100 orang passengers yang masuk ke area security checking. Oleh karena service rate-nya adalah 15 dan lane yang buka ada 3, maka processed passengers maksimum adalah sebesar 45 orang. Di akhir, akan ada sisa 55 orang unprocessed passengers.

Kemudian pada rentang waktu 2, ada 90 orang passengers yang masuk ke area plus 55 orang unprocessed passengers dari rentang waktu 1. Sehingga total passengers yang harus diproses adalah sebesar 145 orang. Oleh karena service rate-nya adalah 15 dan lane yang buka ada 2, maka processed passengers maksimum adalah sebesar 30 orang. Di akhir, akan ada sisa 115 orang unprocessed passengers.

Kemudian pada rentang waktu 3, ada 212 orang passengers yang masuk ke area plus 115 orang unprocessed passengers dari rentang waktu 2. Sehingga total passengers yang harus diproses adalah sebesar 327 orang. Oleh karena service rate-nya adalah 15 dan lane yang buka ada 5, maka processed passengers maksimum adalah sebesar 75 orang. Di akhir, akan ada sisa 252 orang unprocessed passengers.

Begitu seterusnya hingga baris ke 12.

Oleh karena antrian bersifat FIFO (first in - first out), artinya jika saya bisa mengoptimalkan berapa banyak lane yang terbuka, maka saya bisa meminimumkan unprocessed passenger sehingga waktu tunggu antrian akan kurang dari dua rentang waktu (kurang dari 10 menit).

Modelling

Pertama-tama saya akan definisikan decision variables dan beberapa parameter berikut ini:

  • i \in \mathbb{Z}^+, 1 \leq i \leq 12 menandakan rentang waktu satu jam yang dibagi per 5 menit sehingga ada 12 belas kelas.
  • l_i \in \mathbb{Z}^+, 1 \leq i \leq 17 menandakan berapa banyak lane dibuka pada waktu i.
  • sr_i \in \mathbb{Z}^+ menandakan mean service rate semua lane pada waktu i.
    • Artinya: rata-rata banyaknya penumpang yang bisa diperiksa oleh satu orang petugas selama rentang waktu 5 menit.
    • Service rate ini akan dicari dari data yang diberikan.
  • N_i \in \mathbb{Z}^+ menandakan berapa banyak penumpang yang datang ke security check pada waktu i.
  • p_i \in \mathbb{Z}^+ menandakan berapa banyak penumpang yang bisa dan selesai diproses pada waktu i.
  • u_i \in \mathbb{Z}^+ menandakan berapa banyak penumpang yang tidak bisa diproses pada waktu i.
    • Akibatnya jika u_i > 0 akan menambahkan banyaknya penumpang pada i+1.
  • \hat{N}_i \in \mathbb{Z}^+ pada i \in [2,12] menandakan banyaknya penumpang real yang dilayani pada waktu i.
    • Perhatikan bahwa saat i=1 kita dapatkan \hat{N}_1 = N_1.
    • Sedangkan pada i \in [2,12], jika u_{i-1}>0 maka \hat{N}_i = N_i + u_{i-1}.

Tujuan Optimisasi

Tujuan dari model optimisasi ini adalah meminimalkan lane yang dibuka dan unprocessed passengers.

Kelak akan dicoba beberapa objective functions dan akan dibandingkan hasilnya.

Constraints

Maksimal lane yang bisa dibuka setiap waktu i adalah 17.

l_i \leq 17, \space \forall i \in [1,12]

Banyaknya processed passengers bisa jadi kurang dari atau setara dengan service rate dikalikan dengan lane yang dibuka.

p_i \leq sr_i \times l_i, \space \forall i \in [1,12]

Banyaknya unprocessed passengers itu adalah banyaknya passengers masuk dikurangi dengan processed passengers.

u_i = \hat{N}_i - p_i , \space \forall i \in [1,12]

Pencarian Service Rate (sr_i)

Salah satu pertanyaan terbesar pada masalah ini adalah bagaimana mendekati nilai sr_i.

  • Apakah sr_i tergantung dari jam berapa petugas lane bekerja?
  • Apakah sr_i tergantung dari berapa banyak orang passengers yang datang?

Untuk menjawabnya, saya coba analisa sederhana service rate dari data yang diberikan dan buat visualisasi sebagai berikut:

Sebaran Service Rate

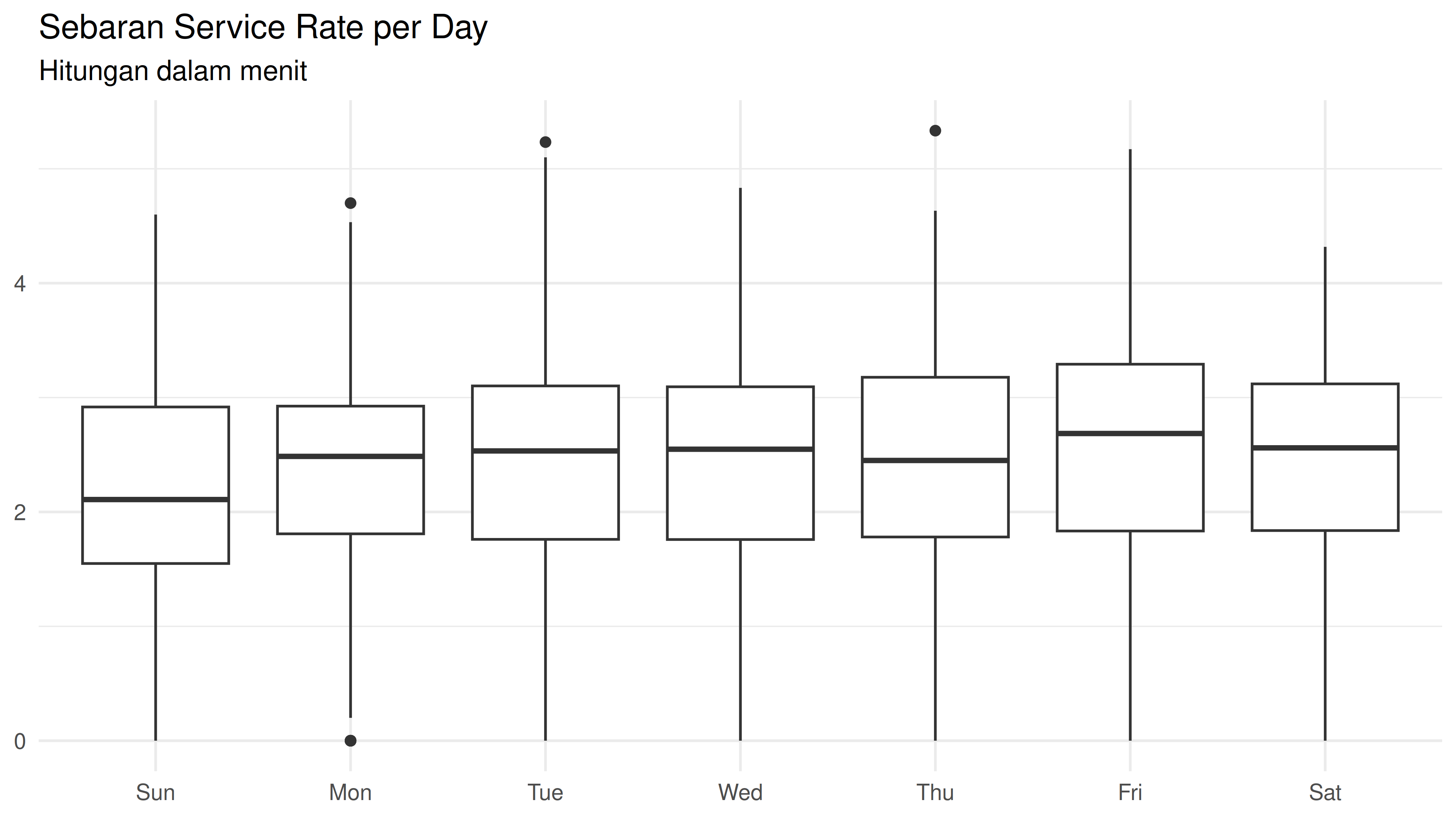
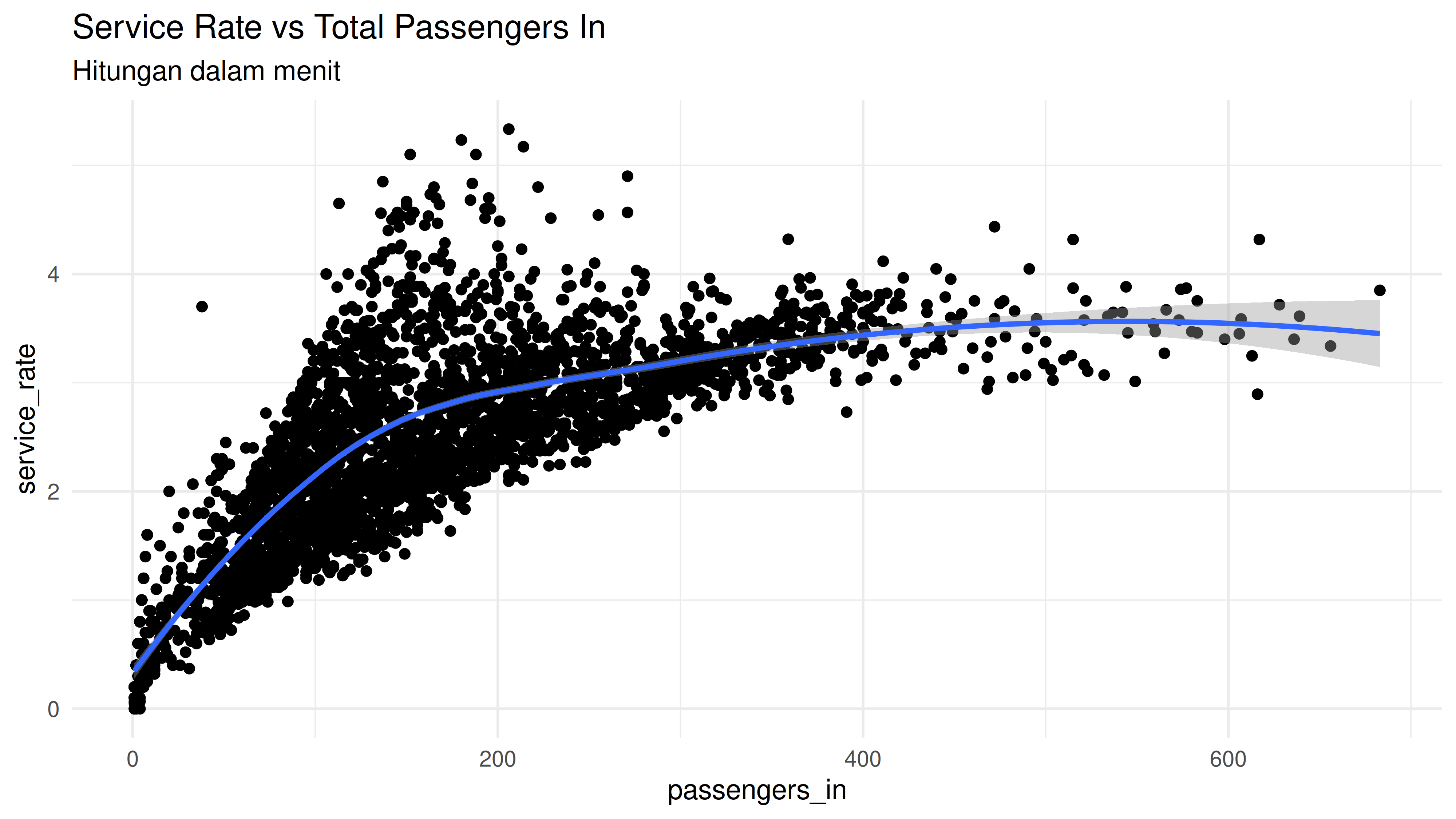
Berikut adalah hubungan antara Service Rate dan total passengers yang masuk:

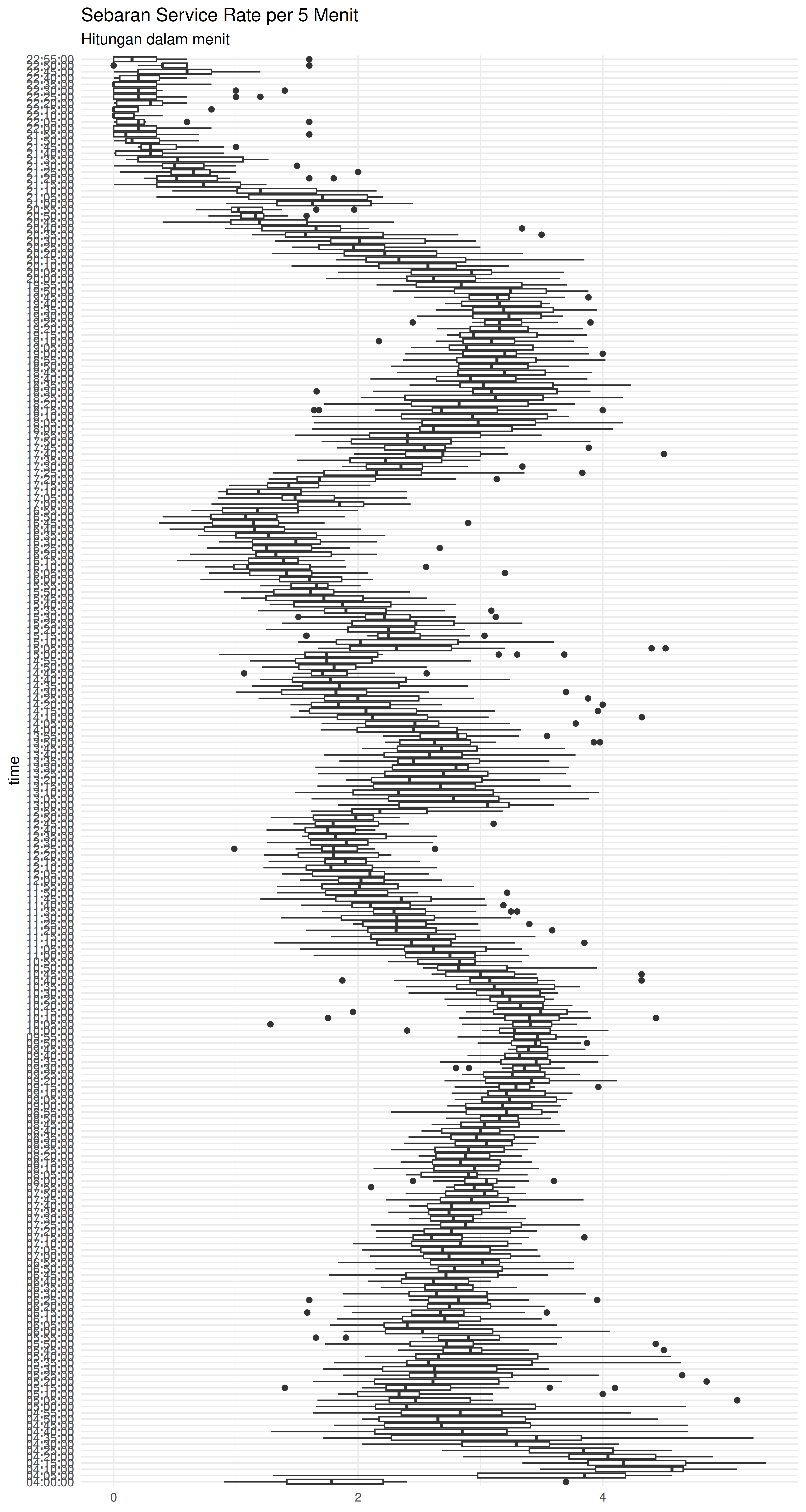
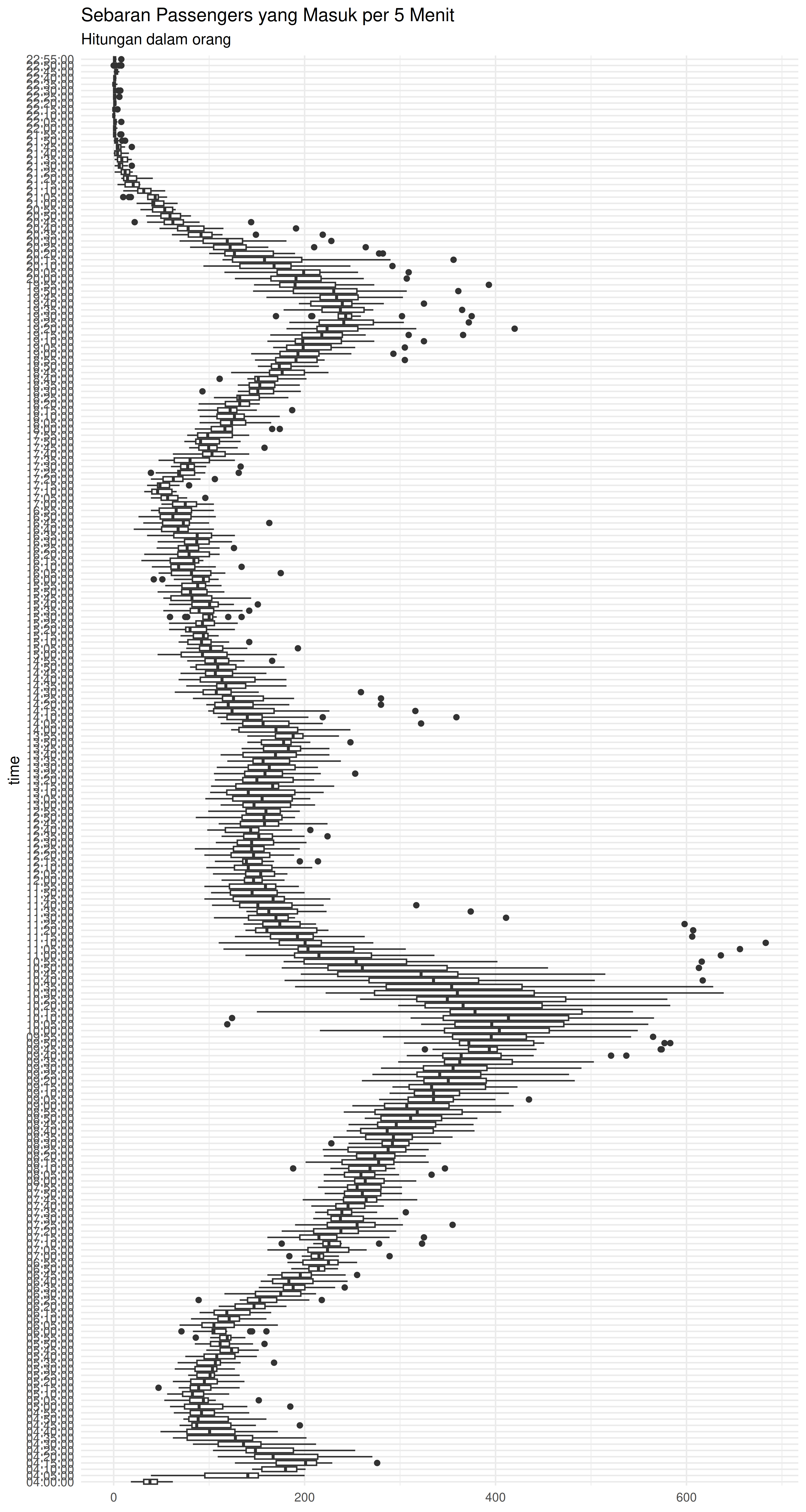
Dari dua grafik yang ditampilkan di atas, kita melihat bahwa ada pola yang mirip antara service rate dengan total passengers jika disajikan dalam timeline yang sama. Dari sini kita bisa mengeliminasi faktor timeline dan bisa menghubungkan langsung antara service rate dan total passengers.

Saat passengers yang masuk antrian membludak, security manager akan memaksa para petugas lane “mempercepat” pekerjaannya (meningkatkan service rate-nya). Namun service rate akan mentok di suatu nilai tertentu dan tak akan bisa naik lagi (manusiawi).

Hubungan Service Rate dengan Total Passengers

Saya bisa membuat model machine learning prediksinya sebagai berikut:

Model Hubungan Service Rate dengan Total Passengers

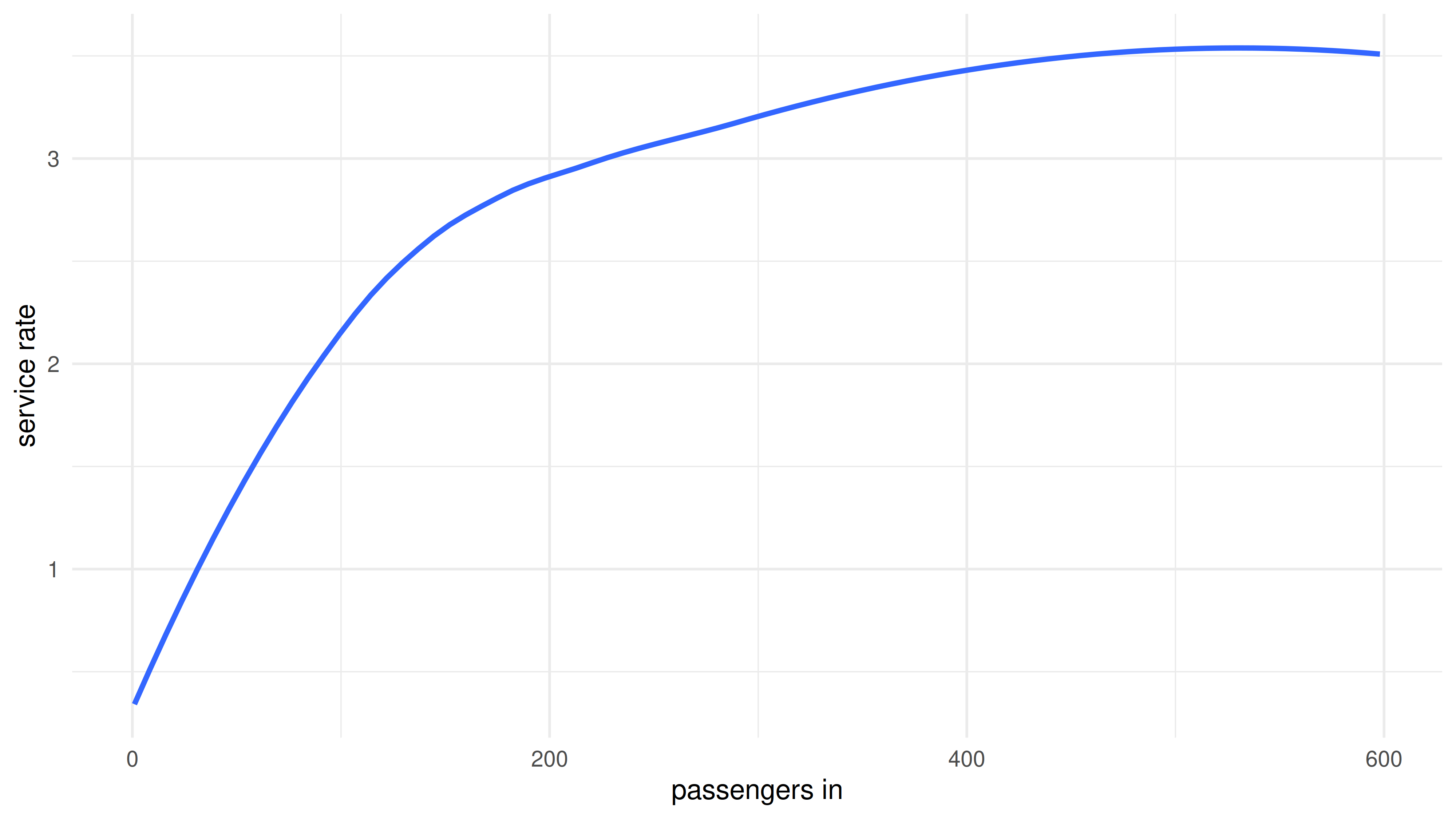
Model ini menghasilkan mean absolute error sebesar 0.409766.

Dua Objective Functions yang Dicoba

Ada dua skenario yang mungkin terjadi:

Skenario I

Security manager berkata:

Jangan sampai ada antrian yang panjang. Atur saja berapa lane yang dibuka atau ditutup!

\min{\sum_{i=1}^{12}{ u_i }}

Skenario II

Security manager berkata:

Dengan petugas seminimal mungkin, pokoknya saya tidak mau tahu, antrian yang ada tidak boleh panjang!

\min{\sum_{i=1}^{12}{ (u_i + 11 \times l_i) }}

Nilai 11 adalah bobot: seorang petugas lane setara dengan 11 orang passengers dalam selang waktu i.

Nilai ini diambil dari expected service rate data.

Semua Constraints yang Ada

l_i \leq 17, \space \forall i \in [1,12]

p_i \leq sr_i \times l_i, \space \forall i \in [1,12]

u_i = \hat{N}_i - p_i , \space \forall i \in [1,12]

Solving the Model

Pencarian solusi optimal dari model menggunakan R dengan metode simplex di library(ompr):

To cite package 'ompr' in publications use:

  Schumacher D (2023). _ompr: Model and Solve Mixed Integer Linear
  Programs_. R package version 1.0.4,
  <https://github.com/dirkschumacher/ompr>.

Hasil Model Skenario I

n_real n_total s_rate lane processed unprocessed
100 100 10.841956 10 100 0
90 90 10.059110 9 90 0
212 212 14.722498 15 212 0
43 43 5.955611 8 43 0
111 111 11.577131 10 111 0
65 65 7.764831 9 65 0
34 34 5.449367 7 34 0
143 143 13.087148 11 143 0
98 98 10.694036 10 98 0
45 45 6.088485 8 45 0
65 65 7.764831 9 65 0
32 32 5.353371 6 32 0 
                 [,1]
min_lane     6.000000
max_lane    15.000000
mean_lane    9.333333
total_antri  0.000000

Hasil Model Skenario II

n_real n_total s_rate lane processed unprocessed
100 100 10.814056 9 97 3
90 93 10.106861 9 90 3
212 215 14.687097 15 215 0
43 43 5.925740 7 41 2
111 113 11.507915 10 113 0
65 65 8.034616 8 64 1
34 35 5.023391 2 10 25
143 168 13.052182 13 168 0
98 98 10.678441 9 96 2
45 47 6.124587 8 47 0
65 65 8.034616 8 64 1
32 33 4.822358 1 4 29 
             [,1]
min_lane     1.00
max_lane    15.00
mean_lane    8.25
total_antri 66.00

Further Discussion: Sensitivity Analysis

Dari paparan model di atas, kita bisa melakukan sensitivity analysis untuk beberapa variabel yang bisa diatur oleh sang security manager.

  • Menurunkan atau menaikkan berapa maksimal lane agar didapatkan nilai optimal secara bisnis.
    • Contoh: tak semua hari petugas yang bertugas bisa lengkap 17 lanes. Barangkali ada yang cuti atau izin bekerja sehingga \leq 17 orang.
  • Menyeragamkan atau membuat standar range nilai service rate sehingga lebih seragam dan “tinggi”.
  • Definisikan berapa banyak unprocessed yang masih diperbolehkan sehingga lane yang digunakan bisa lebih “sedikit”.
  • Menambahkan multi objective optimization sehingga menemukan balance antara lane dan unprocessed.
    • Misalkan mengubah minimize lane menjadi \epsilon - constraint.

if you find this article helpful, support this blog by clicking the ads.

You May Also Enjoy