Updated: SIR Compartment Model

Pendahuluan

Tulisan ini adalah update dari tulisan saya sebelumnya mengenai SIS Model dalam penyebaran COVID-19.

Saya merasa ada beberapa yang harus diupdate terkait perkembangan yang terjadi.

Apa itu?

Update paling utama adalah penggunaan SIR Model yang menurut hemat saya lebih tepat. Apa alasannya?

1. Penjelasan virolog bahwa virus yang dilawan oleh antibodi akan menyisakan cell memory sehingga tubuh akan relatif kebal jika ada virus yang berusaha menginfeksi kembali.
2. Tidak ada penambahan kasus baru di Wuhan karena local transmission sehingga rumah sakit di sana ditutup.

Oleh karena itu, saya akan mengubah model saya yang kemarin dengan SIR Model. Penjelasan detailnya sudah saya tulis di tulisan kemarin yah. Jika belum baca, saya sarankan untuk membacanya sehingga lebih cepat nyambung dengan tulisan ini.

SIR Model

Sekarang kita akan membangun SIR Model yang dimodifikasi yah.

Berikut adalah empat kelompok yang akan dibangun persamaannya?

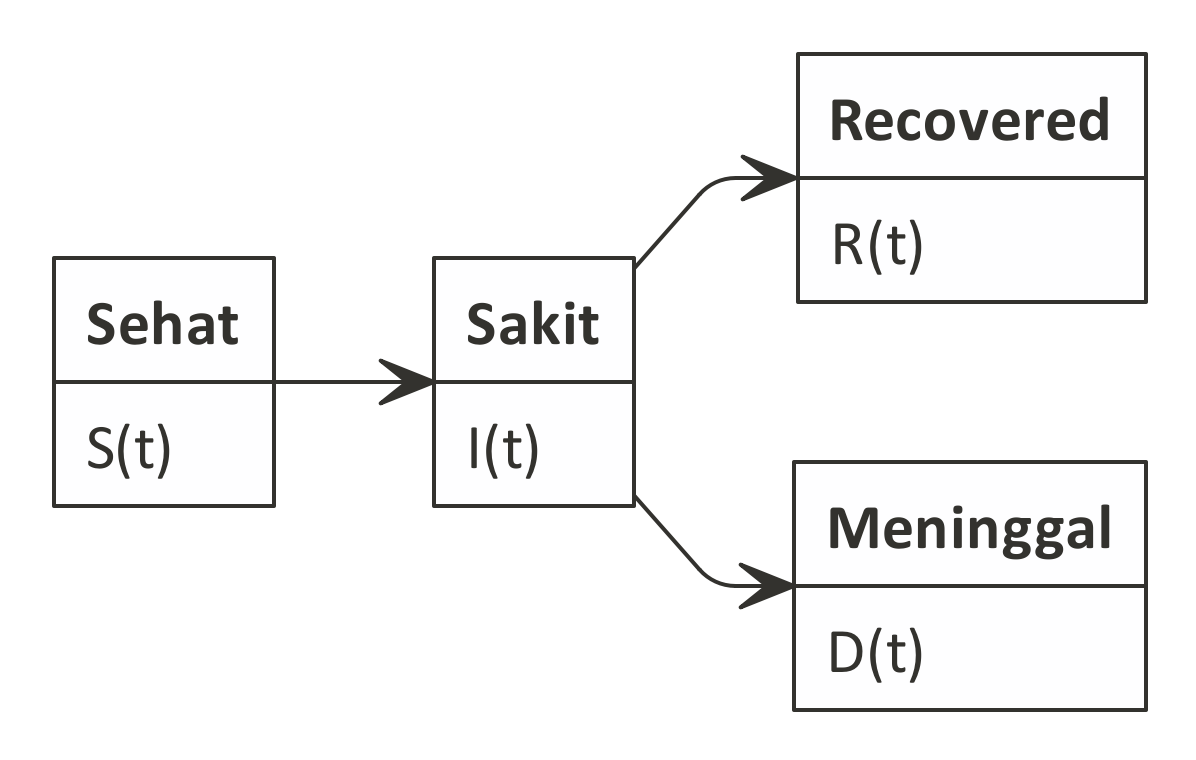
Recovered

Recovered adalah kumpulan orang yang telah sembuh dari penyakit dan dinilai telah resisten terhadap serang virus kembali.

Penambahannya hanya berasal dari orang sakit yang telah sembuh karena belum ada vaksin yang bisa menangkal penyakit ini.

Menaksir Parameter Model

Berdasarkan uraian di atas, maka persamaan diferensial untuk model saya adalah sebagai berikut:

Untuk menaksir parameter, saya akan menggunakan data dan informasi publik yang tersedia. Jika ada data yang berada dalam range, maka saya akan gunakan expected value dari data range tersebut.

Expected value yang saya ambil adalah nilai tengah dari range tersebut.

Menaksir 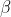, , 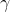dan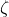

Saya masih akan menggunakan sumber data yang sama dengan sebelumnya untuk menaksir parameter yang ada.

• = 0.059.
• = 0.156.
• = 8.0410^{-4}.

Menyelesaikan Model Persamaan Diferensial

Berdasarkan penaksiran parameter tersebut, untuk menyelesaikan persamaan ini, saya menggunakan R dengan packages deSolve.

library(deSolve)
SIR.model <- function(N,I,t, b, g, z){
  require(deSolve)
  init <- c(S=(N-I)/N,I=I/N,D=0,R=0)
  parameters <- c(bet=b,gamm=g,zet=z)
  time <- seq(0,t,by=t/(2*length(1:t)))
  eqn <- function(time,state,parameters){
    with(as.list(c(state,parameters)),{
      dS <- -bet*(S)*I 
      dR <- gamm*I
      dI <- bet*S*I - gamm*I - zet*I 
      dD <- zet*I
      return(list(c(dS,dI,dD,dR)))})}
  out<-ode(y=init,times=time,eqn,parms=parameters)
  out.df<-as.data.frame(out)
  
  subtit <- bquote(list(beta==.(parameters[1]),
                        ~gamma==.(parameters[2]),
                        ~zeta==.(parameters[3])))
  
  ggplot(out.df,aes(x=time))+
    ggtitle(bquote(atop(bold(.(title)),atop(bold(.(subtit))))))+
    geom_line(aes(y=S,colour="Susceptible"),size=1.5)+
    geom_line(aes(y=I,colour="Infected"))+
    geom_line(aes(y=D,colour="Death"))+
    geom_line(aes(y=R,colour="Recovered"))+
    labs(x = 'Waktu dalam hari',
         y = 'Proporsi',
         title = 'Simple SIR Model',
         caption = 'Solved and Visualized\nusing R\nikanx101.github.io',
         subtitle = subtit) +
    theme(legend.position='bottom')+
    theme(legend.title=element_text(size=12,face="bold"),
          legend.background = element_rect(fill='#FFFFFF',
                                           size=0.5,linetype="solid"),
          legend.text=element_text(size=10),
          legend.key=element_rect(colour="#FFFFFF",
                                  fill='#C2C2C2',
                                  size=0.25,
                                  linetype="solid"))+
    scale_colour_manual("Compartments",
                        breaks=c("Susceptible","Infected",'Death','Recovered'),
                        values=c("blue","red",'black','green'))
}

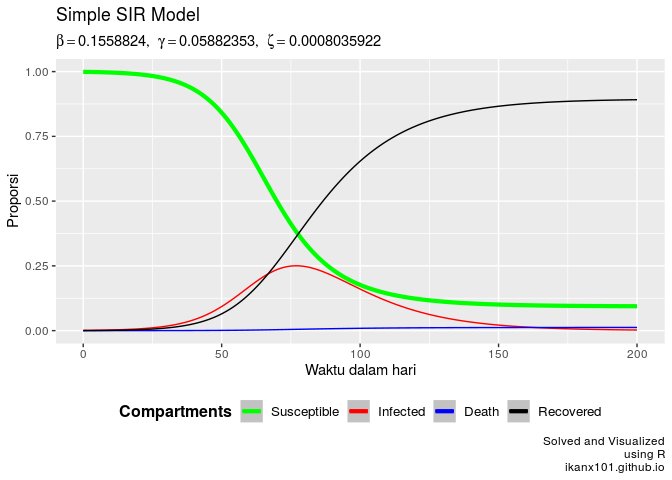
Misalkan dalam satu lingkungan berisi 1000 orang dengan 999 orang sehat dan 1 orang yang sakit, maka kondisinya dalam 200 hari menjadi sebagai berikut:

SIR.model(1000,1,200,beta,gamm,zeta)

Simulasi untuk Berbagai Nilai Parameter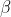

Kita tahu bahwa nilai R0 berada pada range tertentu. Oleh karena itu, saya akan coba simulasi untuk beberapa nilai R0 tersebut.

Simulasi pada saat R0 max

beta_max = 3.9 * gamm
SIR.model(1000,1,200,beta_max,gamm,zeta)

Simulasi pada saat R0 min

beta_min = 1.4 * gamm
SIR.model(1000,1,750,beta_min,gamm,zeta)

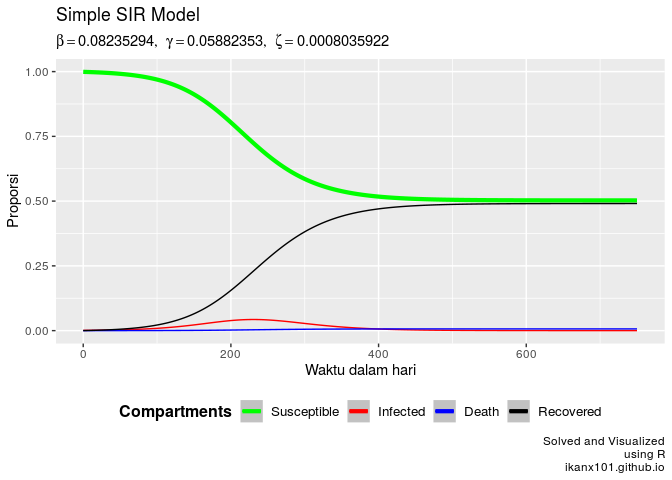
Simulasi saat berbeda-beda di 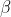maximum

Saat

SIR.model(1000,10,200,beta_max,gamm,zeta)

Saat

SIR.model(1000,15,200,beta_max,gamm,zeta)

Saat

SIR.model(1000,20,200,beta_max,gamm,zeta)

Saat

SIR.model(1000,25,200,beta_max,gamm,zeta)

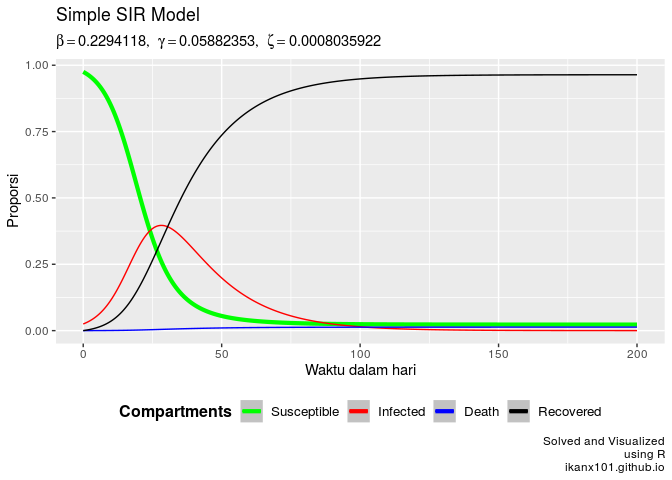
Saat

SIR.model(1000,40,200,beta_max,gamm,zeta)

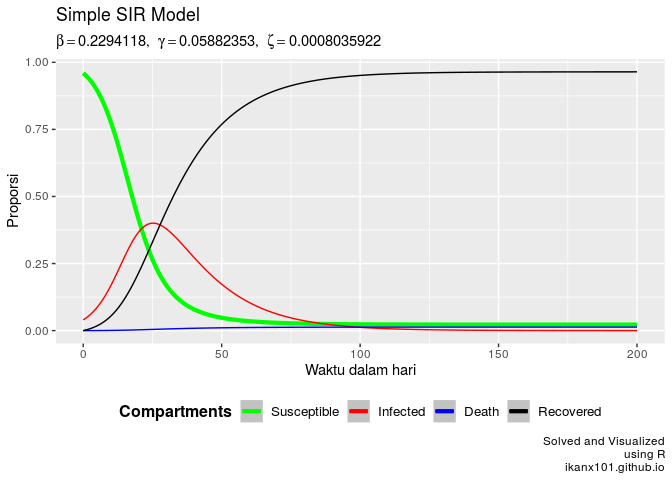
Saat

SIR.model(1000,100,200,beta_max,gamm,zeta)

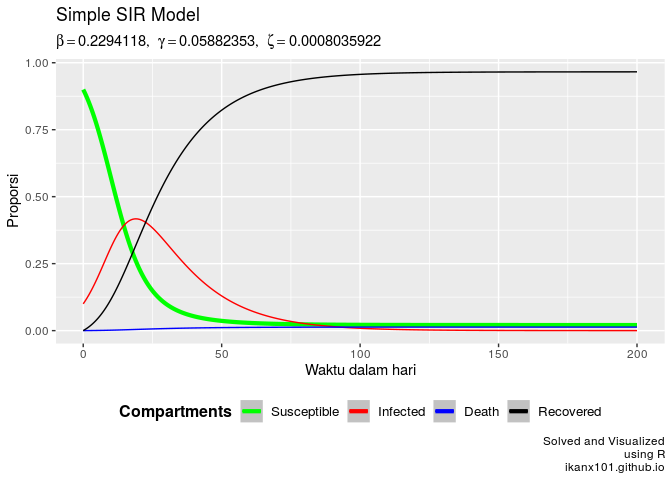
Saat

SIR.model(1000,150,200,beta_max,gamm,zeta)

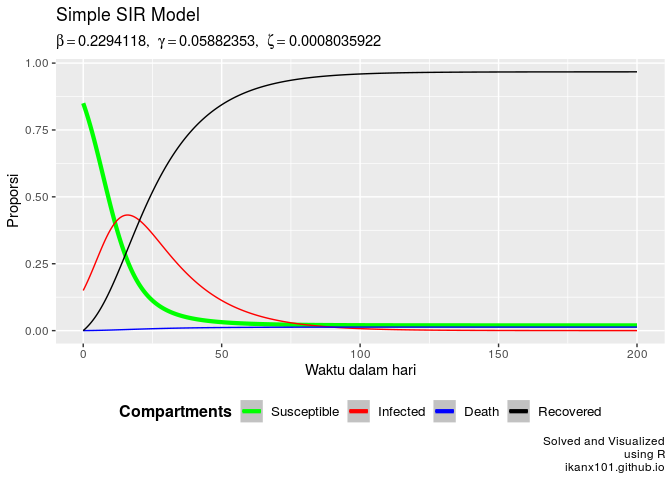
Perbedaan nilai mempengaruhi seberapa cepat wabah menyebar tapi tidak menjadikan puncak semakin tinggi.

Kesimpulan Sementara

Update model kali ini memberikan gambaran bahwa orang yang sakit akan mencapai peak position di sekitar 40% populasi.

Tapi perlu diperhatikan bahwa semua orang sehat akan terinfeksi pada akhirnya dan menjadi resisten dengan waktu relatif cepat (sekitar 30 hari).

Dengan mempertimbangkan maksimum kapasitas fasilitas dan tenaga kesehatan yang ada saat ini, saya tetap menghimbau agar kita harus melakukan langkah konkrit untuk menurunkan dengan gerakan social distancing dan WFH.

---

Komentar Lainnya

Persentase Bisa Menipu

Di awal-awal penanganan COVID-19 di Indonesia, kita mendengar beberapa pejabat dan politisi yang berkata bahwa tingkat kematian akibat COVID-19 ini relatif kecil, hanya ~3% saja.

Persentase itu masih lebih kecil dibandingkan SARS dan MERS. katanya…

Dengan data yang ada sampai saat ini, tentunya pernyataan tersebut tidak salah tapi kurang bijak. Kenapa begitu? Secara psikologi, penyampaian pernyataan tersebut tanpa disadari membuat sebagian masyarakat meremehkan penyakit ini. Gak percaya? Lihat aja lokasi wisata di Puncak dan Pantai Carita beberapa saat lalu.

Coba deh cari informasi berapa angka absolut kematian antara COVID-19, SARS, dan MERS lalu coba kalian bandingkan.

Oleh karena itu, akan sangat bijak saat kita melihat nilai absolut dari kasus kematian yang ada.

Kenapa Mortality Rate di Indonesia Tinggi?

Ada hal yang cukup mencengangkan terjadi di Indonesia. Mortality rate dari COVID-19 sudah menembus angka ~10%. Salah satu yang tertinggi di dunia.

Mengapa demikian?

Berdasarkan pendapat para ahli, COVID-19 sendiri tidak bisa menimbulkan kematian namun komplikasi yang menyertainya yang bisa menimbulkan kematian.

Angka ini sendiri menurut saya menjadi cerminan buruknya kualitas kesehatan bangsa Indonesia sebagai individual.

Ada yang bisa bantu carikan hasil Riskesdas terbaru terkait kondisi kesehatan tersebut di atas?

Bukan Terdistribusi Normal tapi Terdistribusi Pareto!

Kita tahu bahwa COVID-19 ini lebih berbahaya bagi warga senior.

Saya menduga bahwa data ini terdistribusi pareto, tidak berbentuk bell curved. Ini akan saya jadikan bahan tulisan di blog selanjutnya yah.

Stay safe dan stay healthy yah.