Menentukan Kapan Harus Mengganti Lampu Menggunakan Survival Analysis
Pada tahun ini, saya kembali akan melakukan survey panelis untuk melihat customer churn di beberapa produk. Terakhir kali saya memegang project semacam ini adalah pada saat saya masih bekerja di market research consultant / agency pada tahun 2010-2012.
Saat sedang mempersiapkan proposal risetnya, saya coba iseng bertanya ke salah satu GenAI untuk menuliskan analysis plan-nya.
Dari sekian banyak analysis plan yang dia berikan, ada satu analisa yang ternyata belum pernah sama sekali saya gunakan sepanjang karir saya, yakni survival analysis.
Oleh karena itu, pada tulisan kali ini saya akan coba bahas apa itu survival analysis dan apa aplikasinya.
Survival analysis adalah salah satu cara pintar untuk menghitung berapa lama waktu yang dibutuhkan sampai suatu event terjadi.
Bayangkan kita mulai dari titik awal, seperti saat anak kecil pertama kali diberikan mainan baru. Kemudian kita mengamati dan menunggu dengan sabar sampai mainan itu dilempar dan rusak, yang dalam statistik sering disebut sebagai “kegagalan” (failure).
Namun, dalam dunia nyata seringkali kita tidak tahu kapan persisnya mainan itu akan rusak karena adakalanya kita berhenti melihat anak itu.
Misalnya saya sedang menunggu sebuah balok kayu jatuh, tetapi saya harus pergi tidur padahal baloknya masih berdiri tegak. Kita tahu balok tersebut bertahan setidaknya sampai jam tidur saya, tetapi kita tidak tahu kapan persisnya ia akan benar-benar jatuh nanti.
Kita menggunakan probabilitas survival untuk menebak: “Seberapa besar peluang mainan tersebut masih bagus setelah dua jam bermain?”. Ada juga yang namanya waktu survival median, yaitu titik waktu di mana tepat setengah (50%) dari semua mainan di dalam ruangan sudah rusak.
Selain itu, kita bisa melihat hazard yaitu seberapa besar risiko mendadak bahwa sesuatu akan rusak pada detik ini juga padahal ia masih baik-baik saja sampai saat itu.
Pada prakteknya, survival analysis sering digunakan pada bidang medis untuk menghitung peluang kesembuhan pasien atas suatu pengobatan penyakit tertentu. Namun aplikasi survival analysis sebenarnya bisa digunakan untuk bidang lain seperti sales marketing dan predictive maintenance untuk mesin di pabrik.
Saya akan berikan satu contoh detail mengenai penerapan survival analysis pada kasus penggantian bola lampu di sebuah gedung perkantoran besar.
Studi Kasus Pemeliharaan Gedung: “Umur Pakai Bola Lampu”
Suatu waktu, seorang facility manager di sebuah gedung perkantoran memasang 1.000 bola lampu LED baru di lobi dan di seluruh ruangan:
- Untuk lobi dipasang 500 bola lampu. Di lobi, lampu-lampu ini akan terus menyala selama 24 jam.
- Untuk ruangan kantor dipasang 500 bula lampu. Di ruangan kantor, lampu-lampu hanya dinyalakan di jam kerja saja.
Untuk mengoptimalkan anggaran pemeliharaan, ia melakukan studi survival analysis untuk memahami kapan bola-bola lampu tersebut kemungkinan besar akan rusak dan padam. Oleh karena itu manager tersebut melakukan beberapa tahap berikut ini:
1. Menentukan Titik Awal dan Kejadian (Event)
- Waktu Asal
(
): Studi dimulai pada hari pemasangan lampu secara serentak. Misalkan pada tanggal 1 Januari 2023 pukul 00:00.
- Kejadian Ketertarikan (Event of Interest): Kejadian yang diamati adalah “kematian” atau kerusakan bola lampu (saat lampu berhenti berfungsi).
- Variabel Hasil: Waktu survival diukur dalam jam penggunaan sejak instalasi hingga lampu padam atau rusak.
2. Menghadapi Data Tersensor (Censoring)
Dalam dunia nyata, tidak semua bola lampu akan padam saat Anda melakukan analisis. Misalkan studi dilakukan pada rentang 5.000 jam setelah pemasangan. Setelah waktu studi berakhir, ternyata masih ada lampu yang menyala. Inilah keunggulan analisis survival dalam menangani data yang tidak lengkap:
- Sensor Administratif: Setelah 5.000 jam (studi berakhir), misalkan
ada 600 lampu yang masih menyala. Kita tak pernah tahu kapan
lampu-lampu ini akan padam tapi sudah jelas lampu-lampu ini
bertahan setidaknya 5.000 jam.
- Ini disebut sensor kanan (right censoring).
- Sensor Acak: Pada jam ke-1.000, sebanyak 50 lampu yang masih nyala terpaksa dilepas dan diganti dengan model lain. Meskipun lampu-lampu tersebut belum rusak, data umur mereka selama 1.000 jam tetap berharga dan dihitung sebagai data tersensor.
- Pentingnya Data Tersensor: Jika kita hanya menghitung lampu yang mati saja, kita akan mendapatkan estimasi umur lampu yang salah (terlalu rendah) karena mengabaikan informasi dari lampu-lampu yang awet.
3. Menganalisis dengan R
Menggunakan paket survival di R, manager tersebut memasukkan
data dan melakukan beberapa analisa kunci seperti:
- Fungsi Survival
(
): Menghasilkan kurva yang menunjukkan probabilitas sebuah lampu masih berfungsi setelah waktu tertentu.
- Waktu Survival Median: Ini adalah angka kunci bagi manajer gedung—titik waktu di mana 50% dari seluruh lampu telah padam.
4. Membandingkan Kelompok
Manager tersebut ingin tahu apakah lampu di lobi (yang menyala 24 jam) memiliki ketahanan yang sama dengan lampu di kantor (yang dimatikan di malam hari).
- Menggunakan Uji Log-Rank, kita dapat menentukan apakah perbedaan kurva survival kedua kelompok tersebut signifikan secara statistik atau hanya karena kebetulan.
- Jika data yang dimiliki lengkap, kita juga bisa menggunakan Regresi Cox untuk melihat faktor lain, seperti apakah merek lampu atau suhu ruangan meningkatkan risiko kerusakan secara signifikan.
Sekarang dari cerita tersebut, saya akan tunjukkan data simulasi yang dihadapi oleh manager tersebut.
Pertama-tama, saya akan buat data dummy terlebih dahulu:
rm(list=ls())
library(survival)
library(survminer)
library(dplyr)
library(tidyr)
set.seed(1234) # Agar hasil simulasi konsisten
# 1. Menentukan parameter simulasi
n <- 500 # Jumlah lampu per kelompok
study_end <- 5000 # Studi diakhiri pada jam ke-5000 (Sensor Administratif)
# 2. Membuat data untuk Kelompok Lobi (Risiko lebih tinggi/hazard besar)
# berdistribusi weibull rweibull(n, shape, scale)
time_lobi <- rweibull(n, shape = 2, scale = 3000)
group_lobi <- rep("Lobi", n)
# 3. Membuat data untuk Kelompok Kantor (Risiko lebih rendah/awet)
time_kantor <- rweibull(n, shape = 2, scale = 4500)
group_kantor <- rep("Kantor", n)
# 4. Menggabungkan data
data_lampu <- data.frame(
hours = c(time_lobi, time_kantor),
group = c(group_lobi, group_kantor)
)
# 5. Menerapkan Sensor Kanan (Right-Censoring)
# Jika lampu masih menyala saat studi berakhir (> 5000 jam), status = 0
data_lampu$status <- ifelse(data_lampu$hours > study_end, 0, 1)
data_lampu$hours <- pmin(data_lampu$hours, study_end) #
Berikut adalah sampel datanya:
| hours | group | status | |
|---|---|---|---|
| 57 | 2519.462 | Lobi | 1 |
| 64 | 5000.000 | Lobi | 0 |
| 71 | 4355.690 | Lobi | 1 |
| 203 | 3213.358 | Lobi | 1 |
| 223 | 3491.138 | Lobi | 1 |
| 244 | 1830.599 | Lobi | 1 |
| 499 | 2124.340 | Lobi | 1 |
| 536 | 334.272 | Kantor | 1 |
| 624 | 1970.525 | Kantor | 1 |
| 626 | 1198.530 | Kantor | 1 |
| 726 | 540.779 | Kantor | 1 |
| 799 | 5000.000 | Kantor | 0 |
| 866 | 1315.628 | Kantor | 1 |
| 891 | 1296.025 | Kantor | 1 |
| 962 | 3964.385 | Kantor | 1 |
Kolom status = 0 menunjukkan bahwa lampu tersebut masih nyala sampai
rentang studi berakhir (5.000 jam). Sedangkan status = 1 menunjukkan
bahwa lampu tersebut mati pada hours tertentu.
Sekarang kita akan lakukan survival analysis-nya:
# Membuat objek survival
surv_obj <- Surv(time = data_lampu$hours, event = data_lampu$status)
# Menghitung estimasi Kaplan-Meier berdasarkan kelompok
fit_kelompok <- survfit(surv_obj ~ group, data = data_lampu)
# Menampilkan ringkasan termasuk Median Survival Time
print(fit_kelompok)
Call: survfit(formula = surv_obj ~ group, data = data_lampu)
n events median 0.95LCL 0.95UCL
group=Kantor 500 351 3676 3411 3876
group=Lobi 500 473 2473 2337 2615
Dari tabel di atas, kita bisa melihat bahwa median survival time lampu di lobi lebih singkat daripada lampu di kantor. Artinya pada waktu median tersebut, 50% dari populasi lampu masih nyala. Sang manager bisa menjadwalkan pergantian lampu sebelum median time agar lampu-lampu tidak keburu mati di sebagian besar area gedung.
Apakah perbedaan tersebut signifikan? Berikut adalah Uji log-rank-nya:
# Melakukan Uji Log-rank
uji_perbedaan <- survdiff(surv_obj ~ group, data = data_lampu)
print(uji_perbedaan)
Call:
survdiff(formula = surv_obj ~ group, data = data_lampu)
N Observed Expected (O-E)^2/E (O-E)^2/V
group=Kantor 500 351 511 50.0 137
group=Lobi 500 473 313 81.7 137
Chisq= 137 on 1 degrees of freedom, p= <2e-16
Oleh karena kita dapatkan p-value kecil (mendekati nol – kurang dari 0.05), maka bisa disimpulkan bahwa perbedaan median survival time antara lampu di lobi dan kantor berbeda signifikan. Artinya manager harus membuat dua jadwal berbeda untuk pergantian lampu di dua area tersebut.
Berikut ini adalah kurva survival-nya:
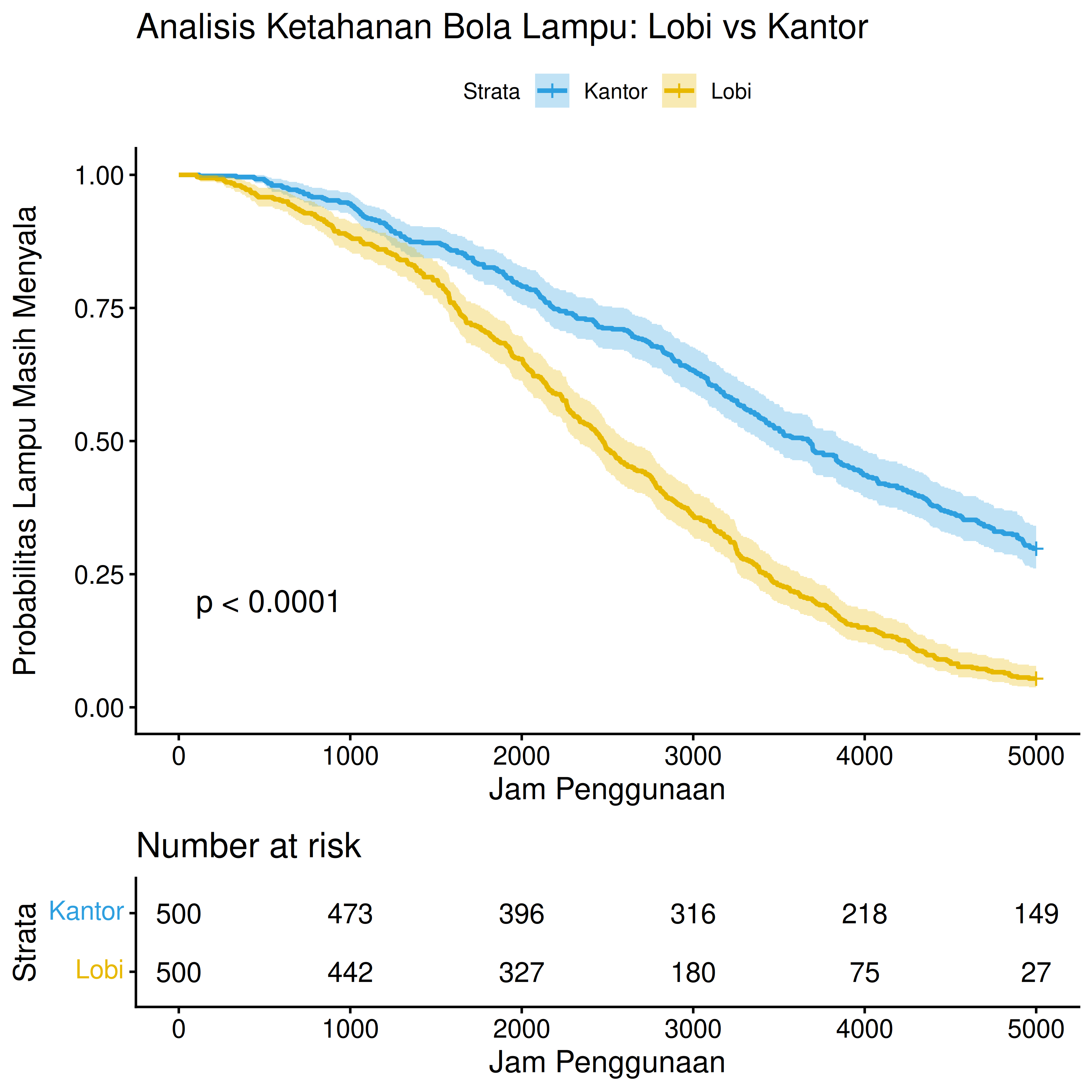
Dari kurva di atas, manager bisa membuat jadwal pergantian lampu yang lebih ketat. Misalkan ia tidak ingin lebih dari 30% lampu padam di area lobi. Berarti ia perlu mencari waktu (jam penggunaan) di mana probabilitas survival-nya 0.7.
Remarks
Berdasarkan uraian di atas, menurut keyakinan saya survival analysis kelak bisa digunakan untuk beberapa business cases yang ada di dunia marketing sales dan manufakturing.
if you find this article helpful, support this blog by clicking the ads.
