Bunch of Ideas, a little bit of Maths.

I am mathematician doing market research and data science

9 minute read

Pada tahun ini, saya dan beberapa rekan di kantor mengadakan training R secara online di kantor. Ternyata animonya luar biasa.

Ibarat kata jualan gorengan, dagangan kami laku keras.

Saking banyaknya pendaftar, tim training HR harus membagi para peserta menjadi beberapa batches.

Saat itu, ada 57 orang yang mendaftar. Sementara kapasitas para trainers untuk satu batch hanya bisa mengajar 12-16 orang saja. Oleh karena itu dibagilah para peserta menjadi 5 batches.

Saat itu, secara manual kami membagi para peserta ke dalam batches tersebut. Para peserta dipilih dan dipilah berdasarkan skor urgensi yang kami nilai secara subjektif sesuai dengan roles pekerjaan masing-masing.

Ternyata menentukan jadwal memang tidak semudah yang dibayangkan.

Pada tulisan sebelumnya, saya telah membahas bagaimana linear programming bisa digunakan untuk menentukan jadwal yang optimal.

Kini, saya akan mengggunakan mixed integer linear programming (MILP) untuk membuat jadwal training. Kasusnya tidak akan mirip persis dengan pengalaman saya tapi akan saya twist agar lebih seru.

Problem

Pada tahun 2021 nanti, tim HR akan melakukan full day training kepada sebagian karyawan. Training ini akan disebar di 4 tanggal di Q1 2021. Training ini cukup diikuti sekali per trainee. Karyawan yang tertarik bisa mendaftar dan memilih sendiri pada tanggal berapa dia bisa mengikuti training tersebut.

  • Sampai detik ini, ada 87 orang karyawan yang mendaftar.
  • Satu kali training hanya bisa diikuti maksimal 22 orang trainee.
  • Ada 4 pilihan tanggal training.
  • Calon trainee bisa memilih 3 dari 4 tanggal yang tersedia. Namun hanya akan dimasukkan ke dalam satu kelas saja.
    • Tanggal pilihan pertama memiliki bobot terbesar. Ini adalah tanggal pilihan utama trainee. Jika jumlah trainee di tanggal ini masih kosong atau mencukupi, maka trainee akan dimasukkan ke dalam kelas tersebut.
    • Tanggal pilihan kedua sebagai alternatif berikutnya.
    • Tanggal pilihan ketiga sebagai alternatif terakhir jika trainee tidak bisa masuk ke dalam tanggal pilihan pertama dan kedua.

Bagaimana cara kita menyusun trainee mana saja yang masuk ke tanggal berapa dari pilihan yang mereka berikan?

a little bit of math

Oke, ini adalah bagian serunya jika kita menyelesaikan linear programming yakni membuat formulasi matematika dari masalah yang ada. Misalkan saya telah mendapatkan data pilihan dari 87 orang tersebut.

## Cuplikan 10 data pilihan trainee

## [[1]]
## [1] 1 4 2
## 
## [[2]]
## [1] 3 4 1
## 
## [[3]]
## [1] 2 3 1
## 
## [[4]]
## [1] 4 3 2
## 
## [[5]]
## [1] 3 4 2
## 
## [[6]]
## [1] 1 3 4
## 
## [[7]]
## [1] 2 3 4
## 
## [[8]]
## [1] 3 1 4
## 
## [[9]]
## [1] 1 2 3
## 
## [[10]]
## [1] 1 4 3

Kita lihat bahwa trainee pertama memberikan pilihan 1, 4, 2. Kita harus memberikan bobot terbesar terhadap pilihan pertama, kedua, dan ketiga. Sementara tanggal yang tidak terpilih, akan saya berikan bobot yang sangat kecil.

Apa gunanya?

Agar kita bisa menjadikan pilihan-pilihan ini menjadi objective function yang harus kita maksimalkan.

Berikut adalah formulasi matematikanya:

n menandakan banyaknya trainee.

n = 1,2,3...,87

m menandakan banyaknya kelas training.

m = 1,2,3,4

Misalkan saya notasikan x_{i,j} adalah bilangan biner (0,1) yang menandakan:

  • 1 jika trainee i mengikuti training di tanggal ke j.
  • 0 jika trainee i tidak mengikuti training di tanggal ke j.

Misalkan saya notasikan w_{i,j} adalah bobot trainee i terhadap training tanggal ke j. Nilai w_{i,j} akan besar saat tanggal yang dipilih merupakah pilihan pertama dan seterusnya.

Objective Function

Kita harus memaksimalkan fungsi berikut:

MAX \sum_{i=1}^{n} \sum_{j=1}^{m} w_{i,j} * x_{i,j}

Constraints

Constraint kapasitas per kelas yang maksimal 22 orang.

\sum_{i=1}^{n} x_{i,j} \leq 22 dengan j = 1,2,3,4.

Constraint seorang trainee harus terpasang ke satu kelas saja.

\sum_{j=1}^{m} x_{i,j} = 1 dengan i = 1,2,3,...,87.

Constraint nilai x_{i,j} \in (0,1) dengan i = 1,2,3,...,87 dan j = 1,2,3,4.

Solusi

Kali ini saya tidak akan menggunakan library(lpSolve) untuk menyelesaikan masalah ini. Saya akan menggunakan OMPR (Optimization Modelling Package in R).

Jadi alih-alih membentuk beberapa matriks, saya akan langsung menggunakan persamaan-persamaan di atas.

# model = MIPModel() %>%
  
  # Definisi x[i,j]: bernilai 1 jika trainee dimasukkan ke training bulan j
#  add_variable(x[i, j], i = 1:n, j = 1:m, type = "binary") %>%
  
  # Maksimalkan objective function
#  set_objective(sum_expr(bobot(pilihan[i], j) * x[i, j], i = 1:n, j = 1:m),
#                "max") %>%
  
  # Constraint kapasitas kelas
#  add_constraint(sum_expr(x[i, j], i = 1:n) <= capacity[j], j = 1:m) %>% 
  
  # Constraint satu trainee hanya boleh masuk ke dalam satu training saja
#  add_constraint(sum_expr(x[i, j], j = 1:m) == 1, i = 1:n)

Setelah saya selesaikan, saya dapatkan konfigurasi sebagai berikut:

training_tanggal_ke banyak_trainee
1 22
2 22
3 21
4 22

Melihat hasil optimal di atas, tidak ada satupun constraint yang dilanggar.

Jika dilihat detailnya, saya akan cek apakah trainee memang dimasukkan ke dalam tanggal sesuai dengan pilihan mereka sendiri atau tidak:

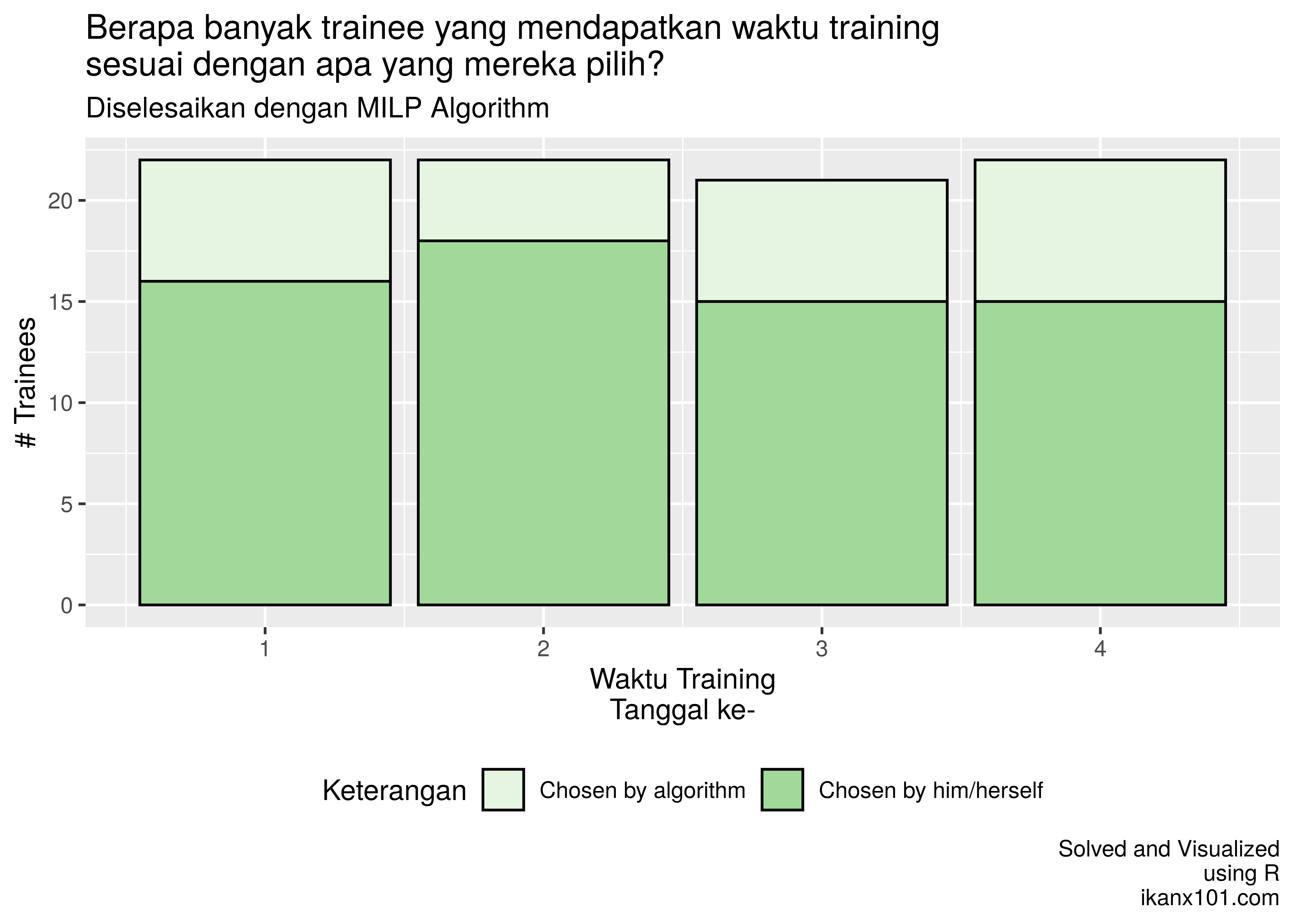
Ternyata ada sebagian kecil dari trainee yang dimasukkan ke dalam training tanggal tertentu bukan berdasarkan pilihan dari mereka.

Hal ini dimungkinkan karena algoritma akan memasukkan trainees yang lebih bisa memaksimalkan objective function sehingga trainee sisa ini dimasukkan ke dalam tanggal tertentu yang tidak melanggar constraints dan tetap memaksimalkan objective function yang ada.

You May Also Enjoy

Geocoding di R Menggunakan tidygeocoder

7 minute read

Di blog ini saya sudah menuliskan berbagai macam metode dan teknik pengambilan data longlat dari alamat (vice versa). Istilah kerennya itu geocoding.