Bunch of Ideas, a little bit of Maths.

I am mathematician doing market research and data science

13 minute read

Bagi rekan-rekan yang pernah mendapatkan mata kuliah analisis data atau statistika dasar, pasti familiar dengan istilah statistika inferensi. Saya mendefinisikannya secara simpel adalah:

Statistika inferensi adalah sekumpulan metode statistik yang digunakan untuk menganalisa data sample untuk kemudian diambil kesimpulannya secara general ke populasinya.

Dari uraian di atas, setidaknya saya highlight ada 3 keywords mendasar, yakni:

  1. Sample,
  2. Populasi, dan
  3. Mengambil kesimpulan.

Apa itu sample? Apa itu populasi?

Saya akan menjabarkannya dengan analogi sensus dan survey agar rekan-rekan lebih mudah memahami.

Misalkan suatu saat saya ingin melakukan penelitian terhadap kebiasaan makan masyarakat Jakarta. Salah satu langkah awal yang wajib saya lakukan adalah mendefinisikan target penelitian ini, yakni warga yang berdomisili di Jakarta.

Populasi dari penelitian ini berarti SEMUA ORANG YANG BERDOMISILI DI JAKARTA. Jika saya melakukan interview kepada semua orang tersebut, maka saya disebut telah melakukan sensus.

Masalah yang saya hadapi adalah: saya tidak memiliki banyak waktu, tenaga, dan biaya untuk melakukan sensus.

Saya hanya mampu meng-interview sekitar 200 orang saja, namun saya harapkan hasil interview-nya cukup mewakili populasi.

200 orang inilah yang disebut sebagai sample.

Statistika inferensi mengambil peranan sebagai alat untuk mengambil keputusan dari data sample untuk di-generalisasi ke level populasi.

Statistika inferensi ada banyak jenisnya, mulai dari uji dua proporsi, uji mean satu sample, uji mean dua sample, dan uji mean tiga atau lebih sample.

Statistika inferensi juga bisa dibedakan menjadi dua, yakni: parametrik dan non parametrik tergantung dari karakteristik data yang kita miliki.

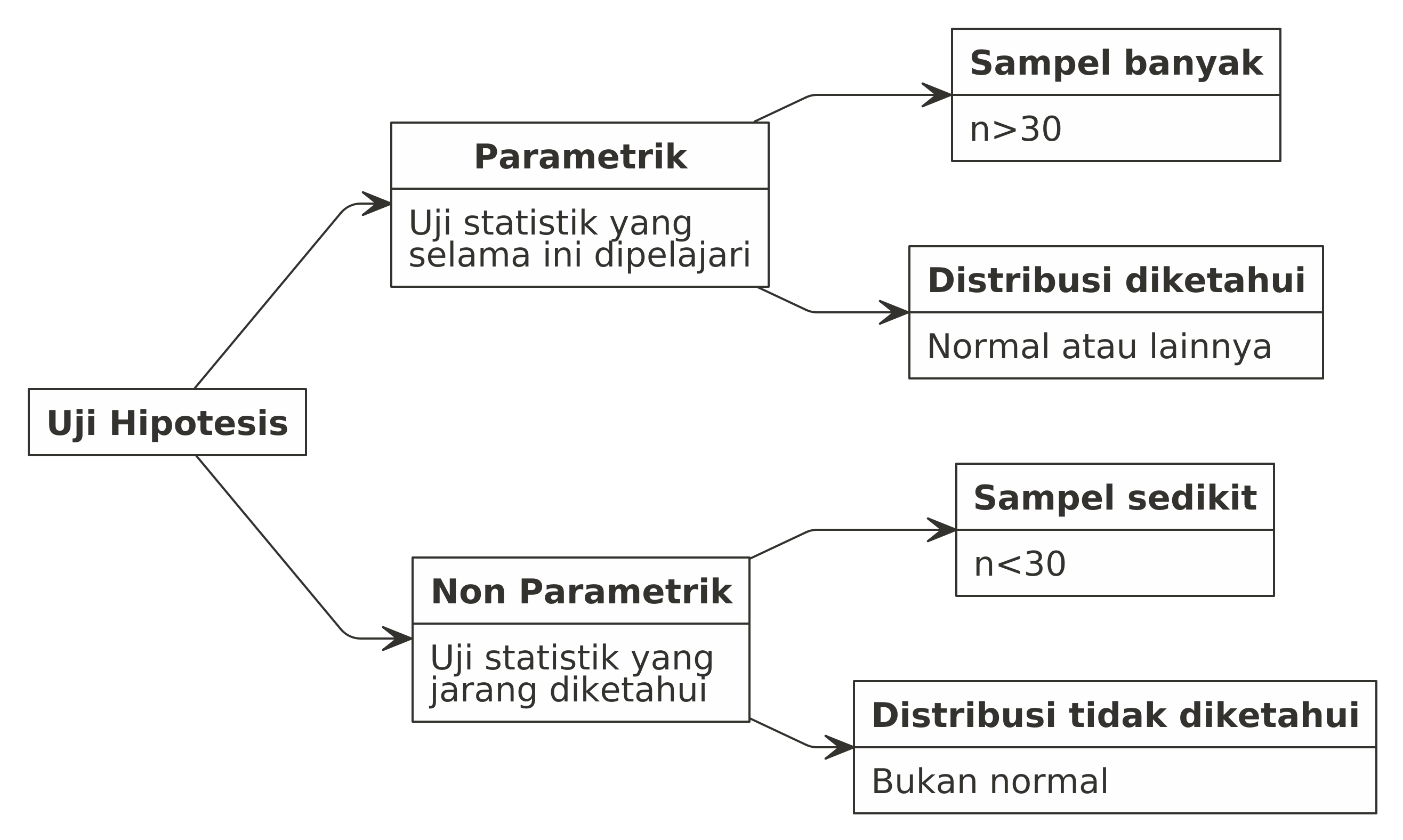
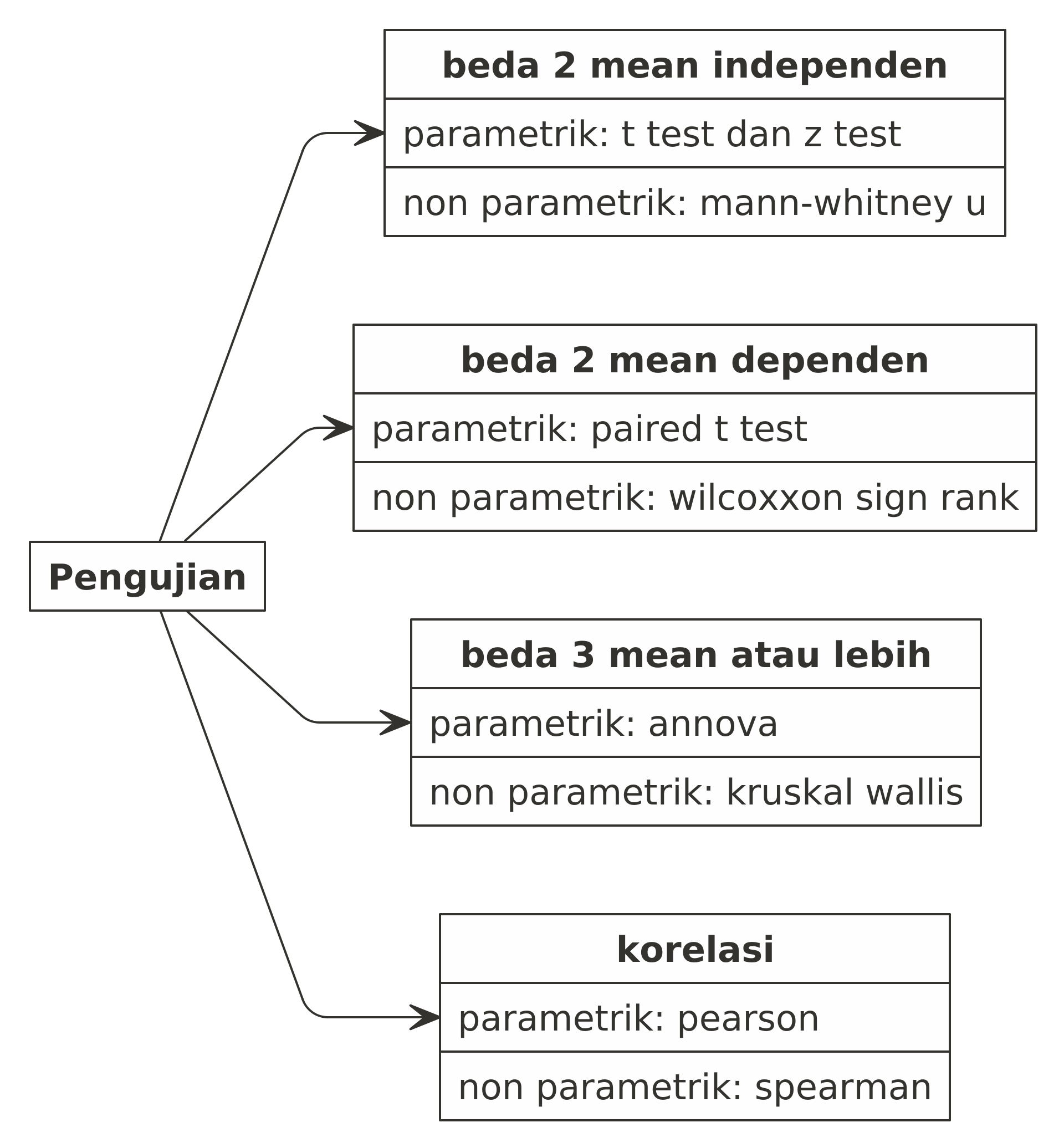
Beberapa waktu lalu, saya pernah menuliskan contoh statistika inferensi non parametrik untuk menguji suatu kasus real di sebuah perusahaan.

Statistika inferensi erat kaitannya dengan pengujian hipotesis. Kelak pengambilan kesimpulan yang dilakukan merupakan hasil pengujian dari hipotesis yang ada.

Sekarang saya hendak mengingatkan kembali bagaimana langkah-langkah yang harus dilakukan untuk melakukan pengujian hipotesis. Saya akan memberikan contoh uji mean dari 2 sample sebagai berikut:

Uji Rata-Rata dari 2 Sample

Masalah

Tim sales di kota A sedang melakukan suatu penelitian. Mereka hendak membandingkan jualan harian dari dua produk minuman:

  1. Minuman A: rasa pepaya,
  2. Minuman B: rasa jambu.

Kedua minuman tersebut memiliki harga, bentuk kemasan (sachet), dan gramasi yang sama.

Untuk itu, mereka mengumpulkan data total sachet terjual dalam sehari selama 60 hari berturut-turut.

Berikut adalah datanya:

## Data Rekapan: Total Sachet Terjual Harian
hari_ke minuman_a minuman_b
1 18 19
2 14 17
3 17 21
4 11 23
5 18 23
6 19 25
7 14 17
8 15 25
9 13 18
10 18 19
11 15 20
12 14 22
13 10 15
14 17 17
15 19 16
16 18 24
17 13 16
18 10 21
19 15 20
20 13 19
21 12 17
22 17 24
23 11 21
24 18 24
25 20 23
26 10 20
27 11 23
28 17 18
29 15 23
30 10 21
31 17 23
32 14 20
33 19 22
34 19 15
35 11 22
36 19 24
37 19 22
38 11 20
39 15 21
40 14 17
41 14 24
42 15 24
43 10 18
44 20 21
45 13 20
46 11 25
47 14 22
48 15 17
49 19 16
50 20 17
51 13 15
52 12 22
53 17 15
54 18 16
55 11 24
56 14 23
57 20 20
58 19 24
59 12 21
60 19 17

Berikut adalah density plot (persebaran data) yang ada:

Langkah-Langkah Uji Hipotesis

Perlu saya ingatkan kembali bahwa uji mean 2 sample ada dua jenis, yakni:

  1. Uji untuk dua data berpasangan: dilakukan jika subjek penelitian sama dan ingin melihat apakah perlakuan yang ada memberikan dampak terhadap perubahan mean data atau tidak. Contoh: peneliti hendak menguji apakah ada perbedaan nilai pre test dan post test dari suatu kelompok murid dalam mengikuti suatu pelatihan. Pada uji ini, kedua sample wajib memiliki jumlah baris yang sama.
  2. Uji untuk data independen: dilakukan jika dua kelompok sample yang diuji tidak saling berkaitan sama sekali. Pada uji ini, tidak ada keharusan jumlah baris data dari kedua sample harus sama (bisa berbeda).

Pada kasus ini, kita akan melakukan uji mean 2 sample yang independen.

Untuk melakukannya, ada dua pendekatan:

  1. Menggunakan z-test: digunakan jika kita mengetahui parameter variansi dari populasi.
  2. Menggunakan t-test: digunakan jika kita tidak mengetahui parameter variansi dari populasi sehingga variansi populasi akan kita dekati dengan variansi dari sample.

Nah, pada t-test ini juga ada dua jenis, yakni: saat kedua variansi diasumsikan sama dan saat kedua variansi diasumsikan berbeda. Oleh karena itu langkah yang proper adalah kita harus mengecek terlebih dahulu apakah kedua sample memiliki variansi yang sama atau berbeda. Sayangnya langkah ini seingat saya tidak ada default function di Ms. Excel.

Jika di R, kita bisa menggunakan function berikut:

var.test(data$minuman_a,data$minuman_b)

Pada kasus ini, variansi dari kedua sample sudah saya set sama. Sehingga kita akan melakukan uji mean 2 sample yang independen menggunakan t-test. Sekali lagi, untuk penyederhanaan, saya asumsikan data yang digunakan berdistribusi normal.

Berikut adalah langkah-langkah uji hipotesis:

  • Tentukan hipotesis nol dan hipotesis tandingan.
    • Notasi: H_0 dan H_1
    • Hipotesis nol adalah hipotesis yang mengandung unsur sama dengan.
  • Hitung statistik uji atau p-value.
  • Kesimpulan: Tolak H_0 jika p_{value} < 0.05.
    • Kenapa dipilih nilai 0.05?
    • Nilai tersebut sebenarnya bisa kita ganti tergantung seberapa besar atau kecil akurasi pengujian yang kita lakukan.
    • Nilai 0.05 yang digunakan biasanya lazim dipakai pada banyak kasus.
    • Penjelasan terkait nilai 0.05 atau \alpha atau yang biasa disebut sebagai significance level bisa rekan-rekan cari di berbagai sumber.
  • Tuliskan kesimpulan dengan kalimat non matematis.

Pengujian Hipotesis

Pertama-tama kita tentukan hipotesis nol dan hipotesis tandingan.

  • Hipotesis nol pada kasus ini adalah: rata-rata sachet terjual dari minuman A dan minuman B sama (tidak ada perbedaan). Notasi: \mu_A = \mu_B.
  • Hipotesis tandingan pada kasus ini adalah: rata-rata sachet terjual dari minuman A dan minuman B berbeda. Notasi: \mu_A \neq \mu_B.

Selanjutnya kita akan hitung p-value. Untuk melakukannya, saya akan menggunakan R dengan perintah mudah sebagai berikut:

t.test(data$minuman_a,data$minuman_b)

## 
##  Welch Two Sample t-test
## 
## data:  data$minuman_a and data$minuman_b
## t = -9.0997, df = 117.56, p-value = 2.765e-15
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -6.331668 -4.068332
## sample estimates:
## mean of x mean of y 
##      15.1      20.3

Kita dapatkan p-value sebesar 2.7647682^{-15}.

Rata-rata sachet terjual dari minuman A adalah: 15.1. Sedangkan rata-rata sachet terjual dari minuman B adalah: 20.3

Jika dibandingkan dengan nilai 0.05, maka didapatkan bahwa p_{value} < 0.05 sehingga kita menolak H_0.

Kesimpulannya:

Rata-rata sachet terjual dari kedua minuman tersebut berbeda. Minuman B terjual lebih banyak dibandingkan minuman A.

if you find this article helpful, support this blog by clicking the ads.

You May Also Enjoy

Geocoding di R Menggunakan tidygeocoder

7 minute read

Di blog ini saya sudah menuliskan berbagai macam metode dan teknik pengambilan data longlat dari alamat (vice versa). Istilah kerennya itu geocoding.