Bisakah Mendapatkan Nilai Bagus pada Ujian dengan Cara Menjawab Asal?

Waktu sekolah dulu (SMP atau SMA), apakah kalian pernah memiliki teman yang selalu mendapatkan nilai bagus saat ujian tapi saat ditanya-tanya, dia hanya bilang:

Gw gak belajar, beruntung aja dapat nilai bagus padahal jawabnya ngasal…

Dulu saya ppernah punya teman yang seperti itu. Saya pribadi sih tidak percaya bahwa itu adalah keberuntungan. Kenapa? Secara simulasi statistik, kita bisa membuktikan pernyataan itu.

---

Perhitungan Matematis

Misalkan saya memiliki 50 pertanyaan ujian berupa pilihan ganda (empat opsi pilihan) dengan hanya satu opsi yang benar.

Secara simpel, kita bisa hitung bahwa peluang seseorang menjawab satu pertanyaan dengan benar_ **secara **_ngasal_ adalah .

Jadi untuk menjawab 50 pertanyaan secara ngasal, kita bisa hitung expected nilai ujiannya sebesar:

Dari hitung-hitungan di atas, kita bisa dapatkan bahwa expected nilai ujiannya adalah sebesar 25.

Pembuktian dengan Simulasi

Perhitungan di atas belum cukup untuk membuktikan pernyataan teman saya tersebut. Kenapa?

Saya perlu menghitung berapa peluang seseorang mendapatkan nilai bagus dengan cara menjawab ngasal!

Lantas bagaimana cara saya menghitung peluangnya?

Saya akan gunakan simulasi Monte Carlo.

Bagaimana cara kerjanya?

Saya akan generate semua kemungkinan nilai ujian yang muncul sebanyak 90.000 kali iterasi dengan ketentuan:

1. Ada 50 soal ujian pilihan ganda.
2. Ada 4 opsi jawaban dengan hanya satu pilihan yang benar.

Dari hasil 90.000 kali iterasi, saya akan buat histogramnya dan kemudian saya akan hitung berapa peluang seseorang mendapatkan nilai bagus.

Saya akan definisikan nilai bagus adalah minimal sebesar 80 (minimal 40 soal terjawab benar dari 50 total soal yang ada).

Berikut hasil simulasi saya:

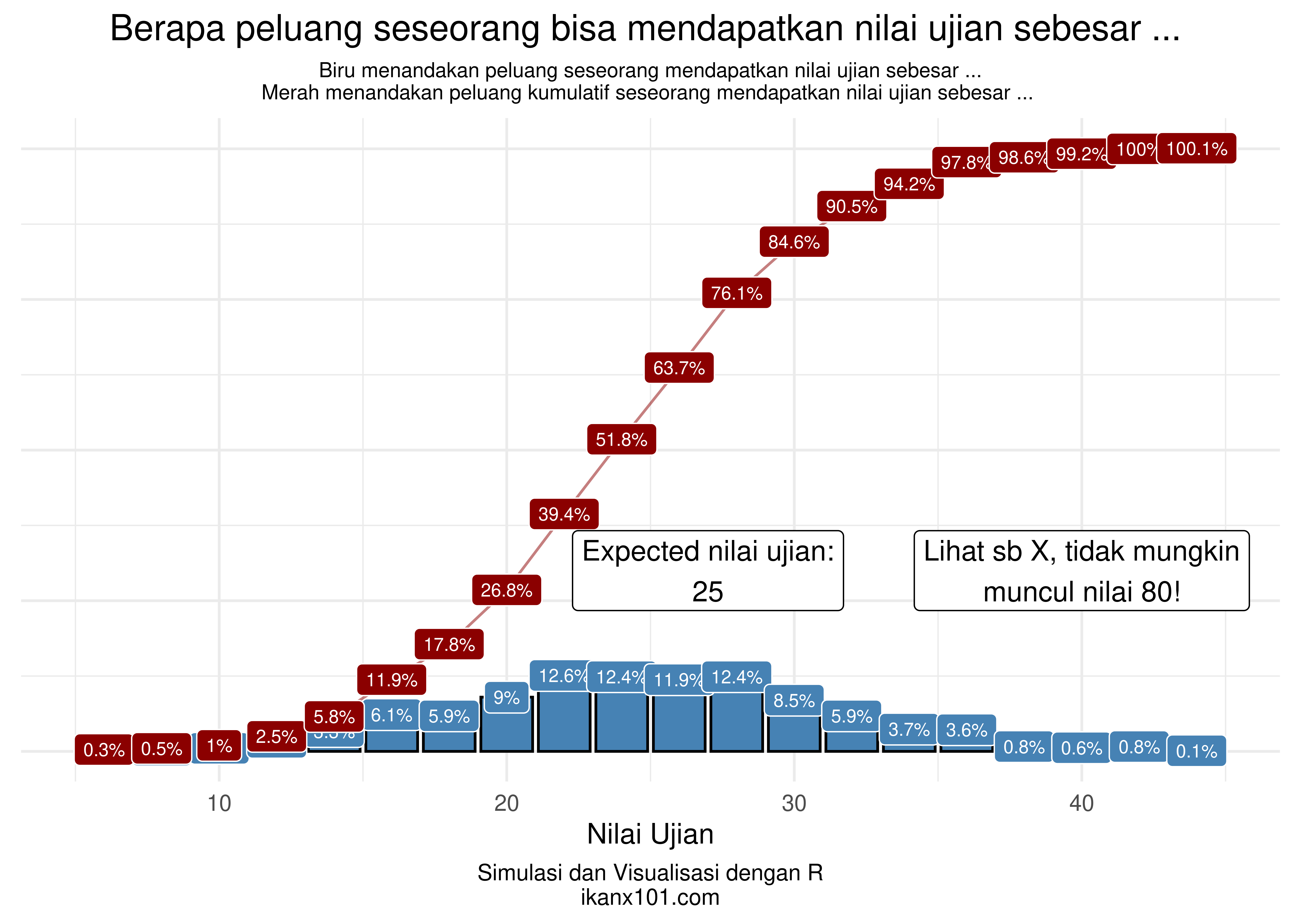
Dilihat dari grafik hasil simulasi di atas, bahwa hampir tidak mungkin seseorang mendapatkan nilai ujian minimal 80.

Peluangnya nol.

Pembuktian dengan Distribusi Binomial

Sebenarnya kasus di atas bisa dipandang sebagai masalah di data berdistribusi Binomial.

Peluang terjadinya event dari total dengan proporsi sukses sebesar .

Untuk kasus ini, maka peluang seseorang mendapatkan nilai bagus adalah:

Peluangnya nol.

---

Kesimpulan

Jadi teman saya sepertinya tidak bisa dipercayai omongannya. hehe

---

if you find this article helpful, support this blog by clicking the ads.