Bunch of Ideas, a little bit of Maths.

I am mathematician doing market research and data science

12 minute read

SOAL 1a

Soal Utama

Diketahui sebuah fungsi:

\frac{(x+1)^2}{16} + \frac{(y-1)^2}{8} = 1

Sub Soal Ia i

Gambarlah fungsi tersebut. Hitunglah luas area di bawah kurva pada kuadran pertama untuk nilai x \in [0, \sqrt{14}-1] dengan metode partisi trapesium.

Jawaban Sub Soal Ia i

Gambar Fungsi Berikut adalah gambar fungsi yang saya buat dengan R.

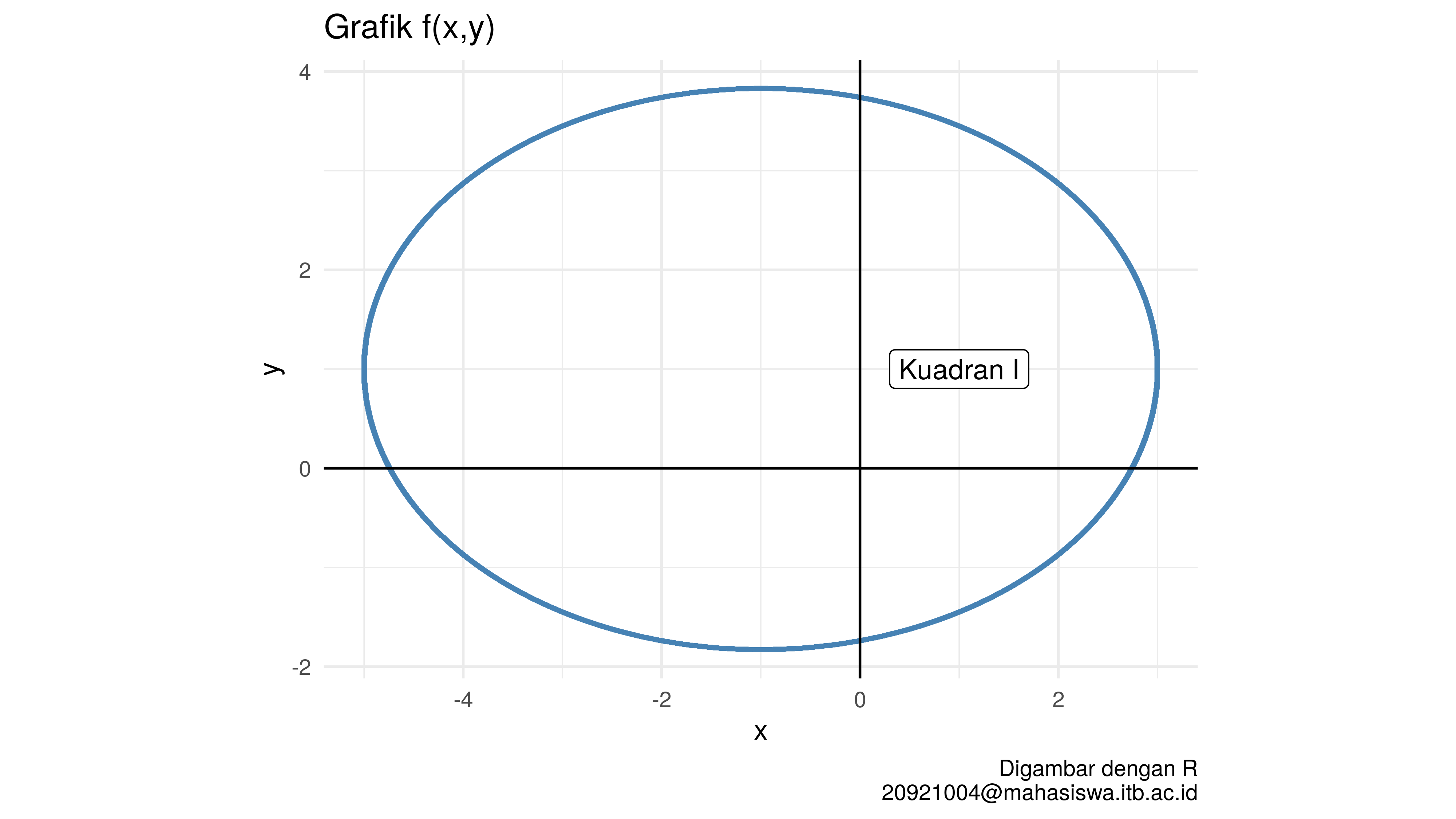
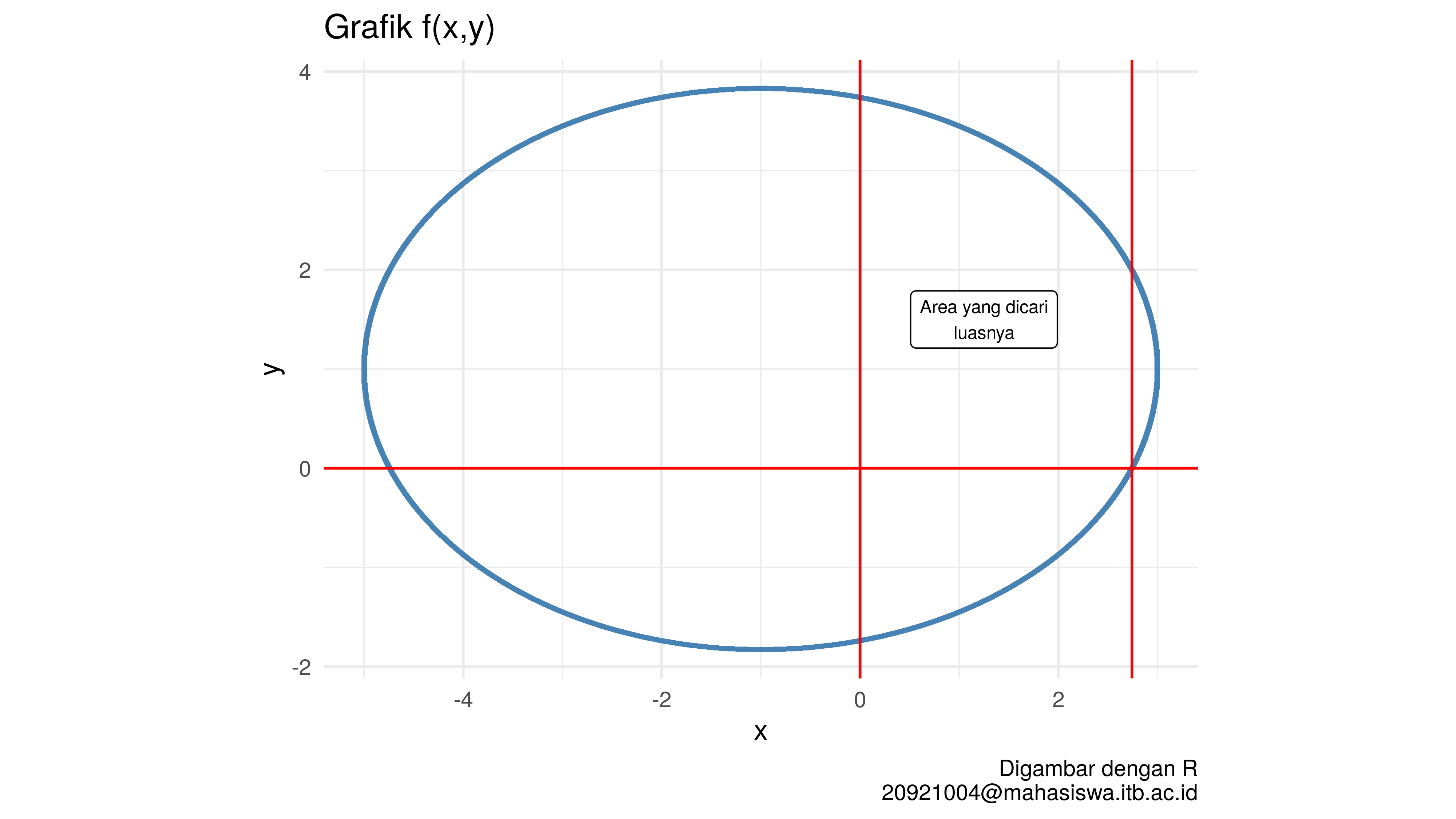
Sekarang kita akan menghitung luas area pada kuadran I di selang x \in [0, \sqrt(14)-1]. Saya akan gambarkan selang tersebut dengan garis merah sebagai berikut:

Mengubah Fungsi Untuk memudahkan, kita perlu memodifikasi fungsi f(x,y) ke dalam bentuk y = g(x) yang lebih sederhana.

y = 1+ \sqrt{8 - \frac{(x+1)^2}{2}}

Karena kita akan menghitung luas area di kuadran I, maka nilai akar yang dihasilkan kita akan ambil hanya yang bernilai positif saja.

Luas Area di Bawah Kurva Ide dasar untuk menghitung luas area di bawah kurva adalah:

L = alas \times tinggi

Pada partisi trapesium, tinggi yang akan digunakan adalah: tinggi = \frac{f(x_1) + f(x_2)}{2}

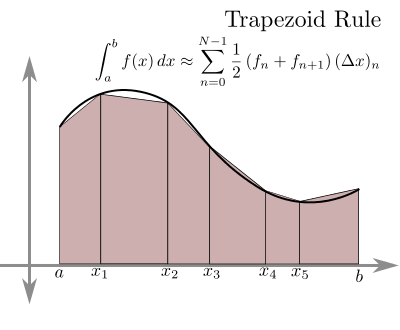
Pada metode trapesium ini, penentuan berapa banyak selang akan mempengaruhi seberapa akurat hasilnya.

Barikut adalah program luastrap yang saya buat di R:

luas_trap = function(x0, # titik awal
                     xn, # titik akhir
                     n,  # banyak selang
                     f){ # fungsi y = f(x)
  # menghitung delta x
  h = (xn - x0) / n
  # menghitung f di x0
  f0 = f(x0)
  # selang pertama
  i = 1
  k = x0 + i*h
  fn = f(k)
  integration = (f0+fn)/2
  # iterasi untuk selang berikutnya hingga selesai
  for(i in 2:n){
    f0 = fn
    k = x0 + i*h
    fn = f(k)
    temp = (f0+fn)/2
    integration = integration + temp
  }
  # menghitung hampiran luas
  integration = integration * h
  return(integration)
}

Sekarang kita akan bandingkan hasilnya untuk berbagai banyak selang.

n banyak selang Luas aproksimasi
10 8.64494288
50 8.65494631
100 8.65526330
200 8.65534260
1000 8.65536798
2500 8.65536887
5000 8.65536899
100000 8.65536904
250000 8.65536904
500000 8.65536904
750000 8.65536904
1000000 8.65536904

Hasil Perhitungan Luas Trapesium

Terlihat bahwa semakin banyak selangnya, hasilnya konvergen ke suatu nilai yang sama yakni: 8.65536904.

Sub Soal Ia ii

Buatlah algoritma dan flowchart untuk menghitung luas soal sebelumnya dengan metode Monte Carlo. Lakukan analisa hasil yang diperoleh dengan jumlah sampling yang diberikan. Anggaplah perhitungan analitis adalah yang benar sehingga merupakan rujukan nilai.

Jawaban Sub Soal Ia ii

Perhitungan Analitis Kita bisa menghitung secara analitis luas area di bawah kurva dengan cara melakukan integral tentu berikut ini:

\int_0^{\sqrt{14}-1} 1+ \sqrt{8 - \frac{(x+1)^2}{2}} \text{ dx} \simeq 8.65536904

Metode Monte Carlo Analogi dari metode ini adalah seperti melempar sekian banyak darts ke suatu target. Luas area di bawah kurva didefinisikan sebagai rasio dari banyaknya darts yang jatuh di bawah kurva dengan total semua darts yang dilempar.

Berikut adalah flowchart-nya:

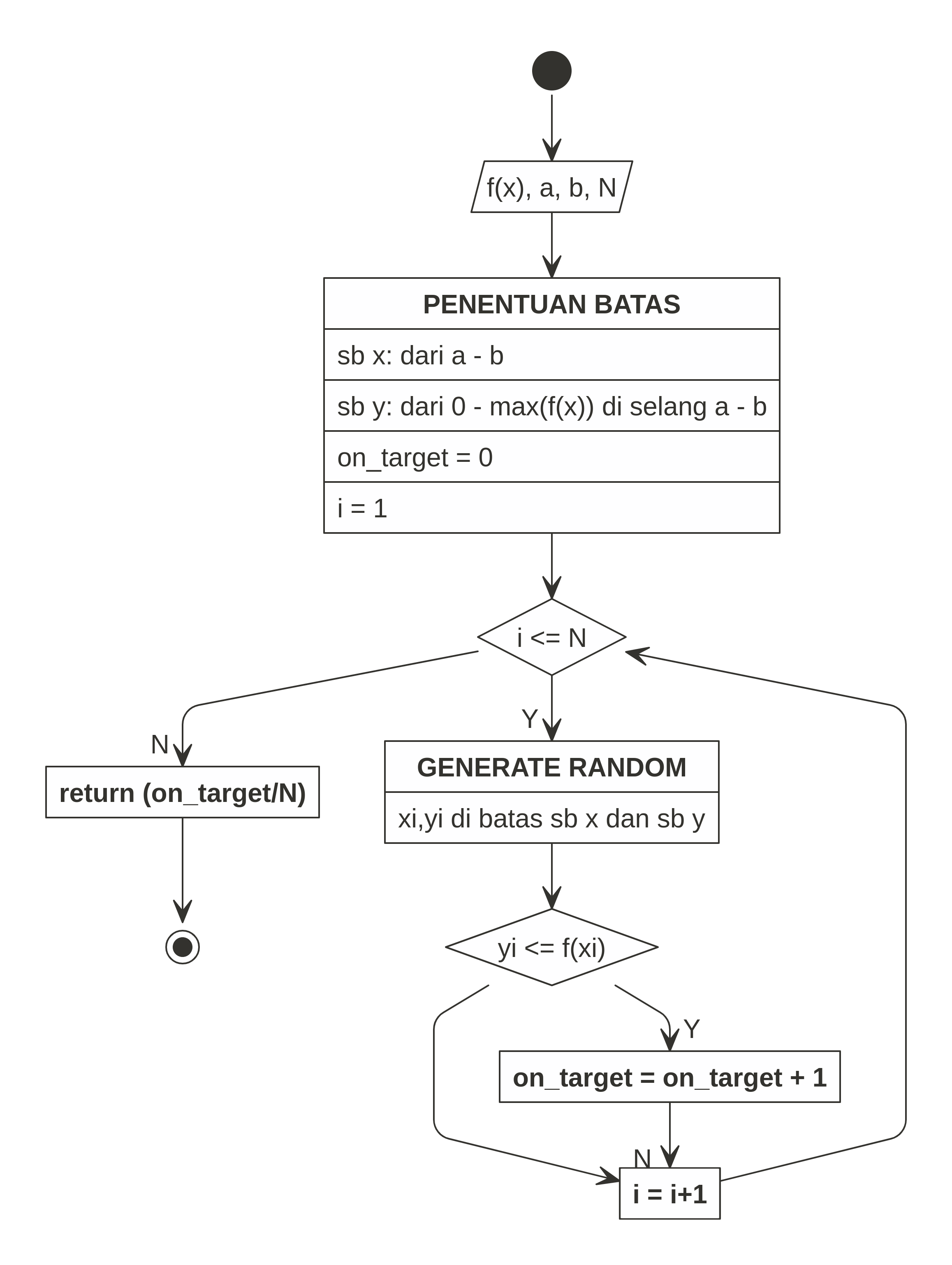
Hal terpenting dalam metode ini adalah mendefinisikan batas titik x,y untuk di-random. Kenapa?

Kita tidak ingin darts yang kita lempar jatuh ke area sembarang! Kita harus definisikan di mana area bermain darts.

Perhatikan kembali grafik di bawah ini:

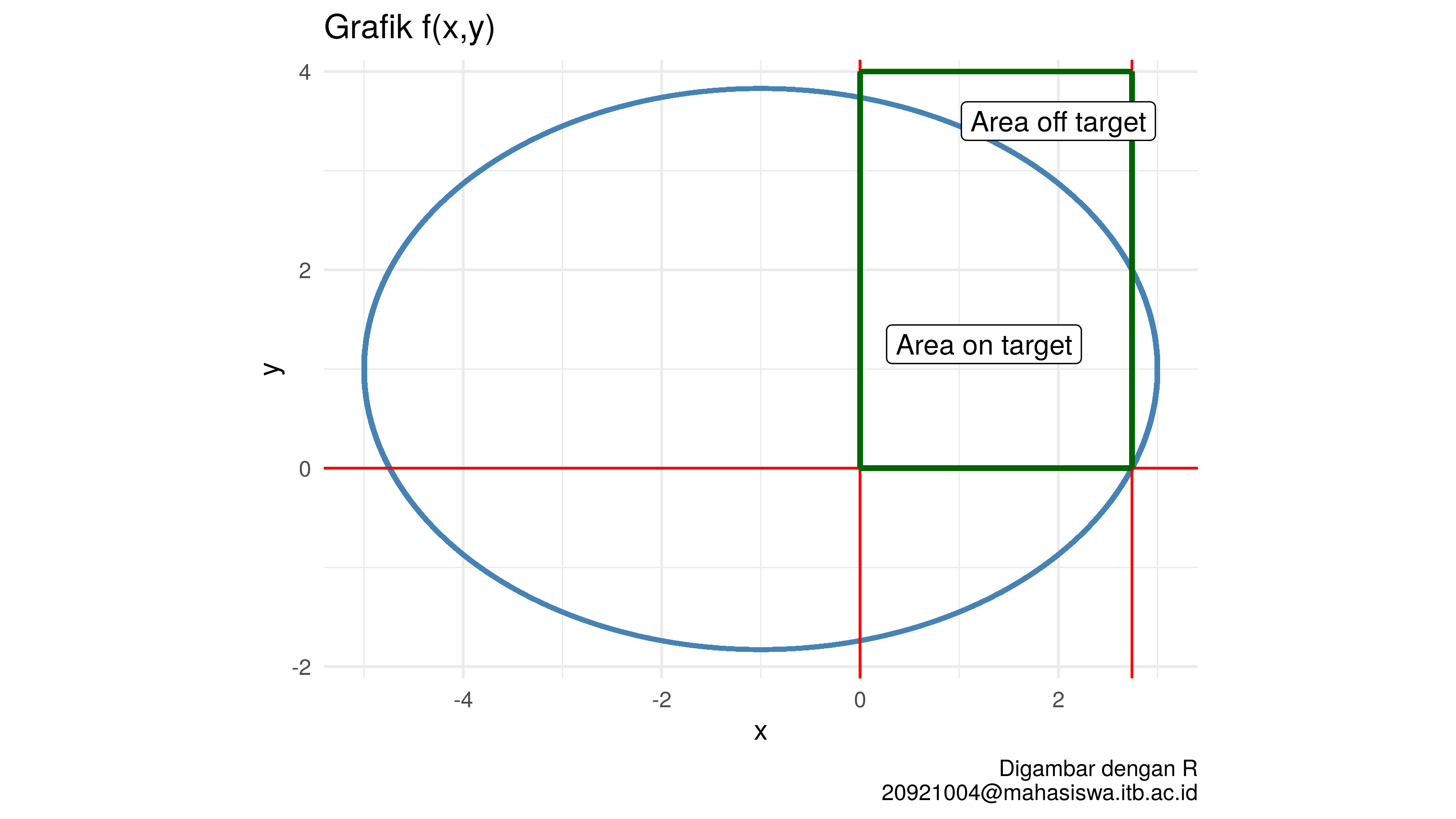
Saya akan menjadikan area di dalam kotak warna hijau sebagai area random titik metode Monte Carlo. Jika titik tersebut jatuh ke bawah kurva, maka akan dihitung sebagai on target. Jika jatuh di atasnya, berarti off target.

Kelak luas akan dihitung dengan cara:

L = 4 \times (\sqrt{14}-1) \times ratio

Berikut adalah programnya dalam R:

brute_force = function(f,x1,x2,y1,y2,N){
  # generating random number
  x = runif(N,x1,x2)
  y = runif(N,y1,y2)
  
  # pengecekan y <= f(x)
  rekap = 
    data.frame(x,y) %>% 
    mutate(f_x = f(x),
           on_target = ifelse(y <= f_x,1,0))
  
  # hitung rasio on target vs all dots
  rasio = sum(rekap$on_target) / N
  # hitung luas
  luas = (x2-x1)*(y2-y1)*rasio
  
  # perbandingan dengan eksak
  eksak = 8.65536904
  delta = abs(eksak - luas)
  
  # output plot
  plot_sim = 
    soal +
    geom_point(data = rekap,aes(x,y,color = on_target)) +
    theme(legend.position = "none") +
    labs(subtitle = paste0("Didapat nilai rasio sebesar ",rasio))
  
  # output
  output = list(
    "Plot Brute Force" = plot_sim,
    "Luas area di bawah kurva" = luas,
    "Absolute selisih dg solusi eksak" = delta
    )
  
  return(output)
}

Saya menghitung error atau selisih solusi numerik dengan solusi eksak dengan cara:

![\Delta = |eksak - numerik|](https://latex.codecogs.com/svg.latex?%5CDelta%20%3D%20%7Ceksak%20-%20numerik%7C “\Delta = eksak - numerik ”)

Sekarang kita akan coba program tersebut untuk N = 100

$`Plot Brute Force`


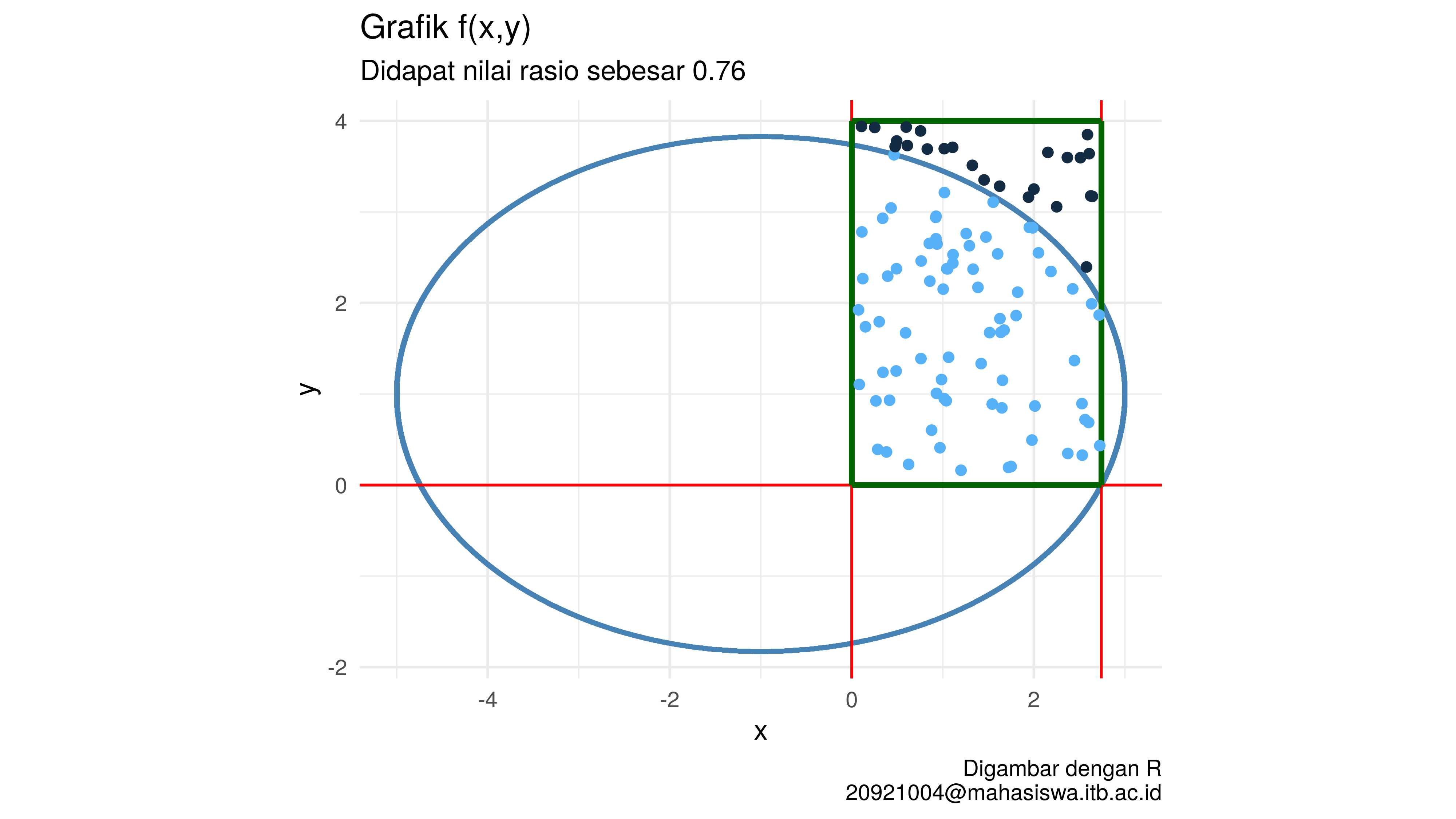
$`Luas area di bawah kurva`
[1] 8.33463846

$`Absolute selisih dg solusi eksak`
[1] 0.320730584

Sekarang kita akan coba program tersebut untuk N = 200

$`Plot Brute Force`


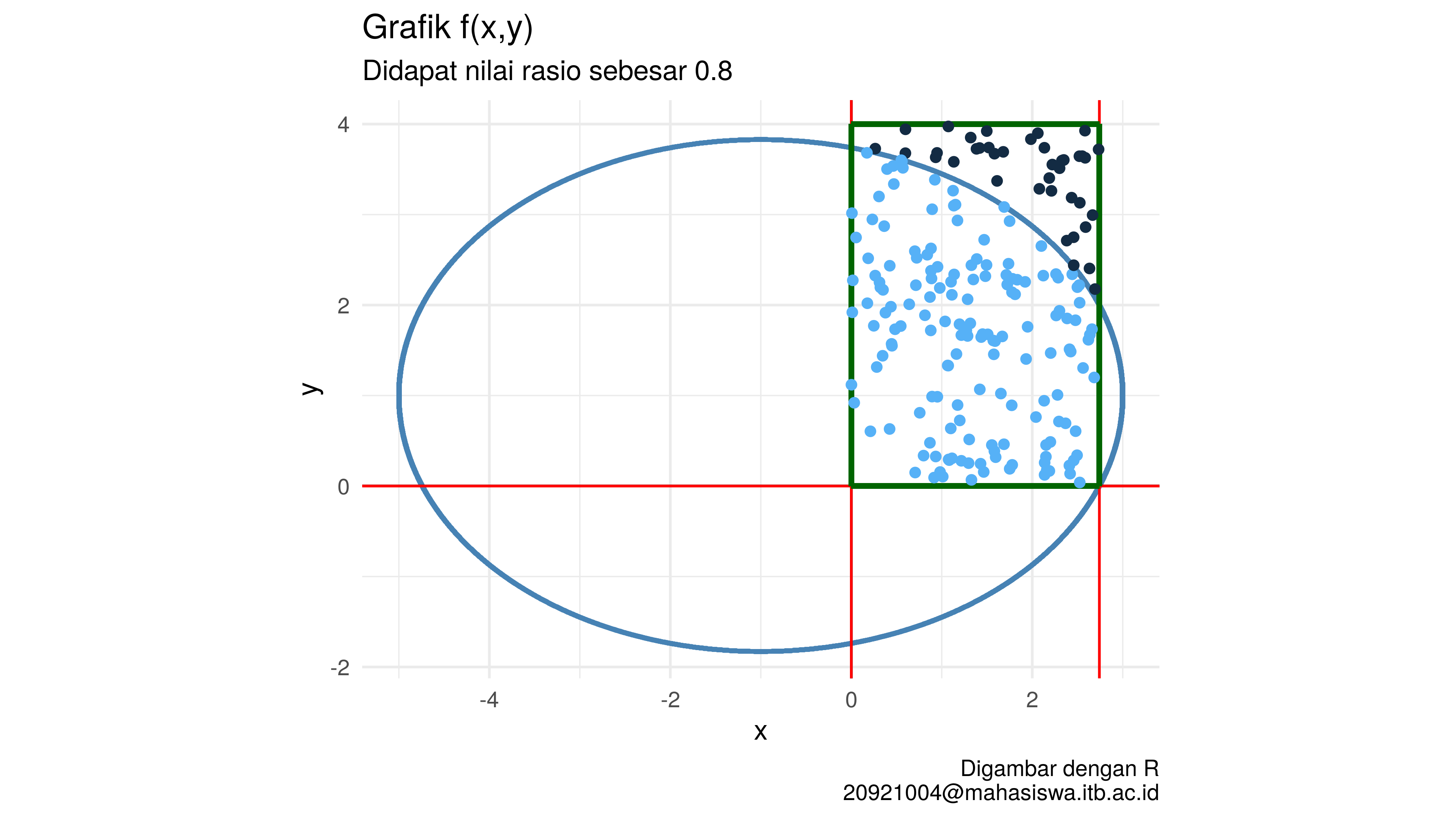
$`Luas area di bawah kurva`
[1] 8.77330364

$`Absolute selisih dg solusi eksak`
[1] 0.117934598

Sekarang kita akan coba program tersebut untuk N = 500

$`Plot Brute Force`


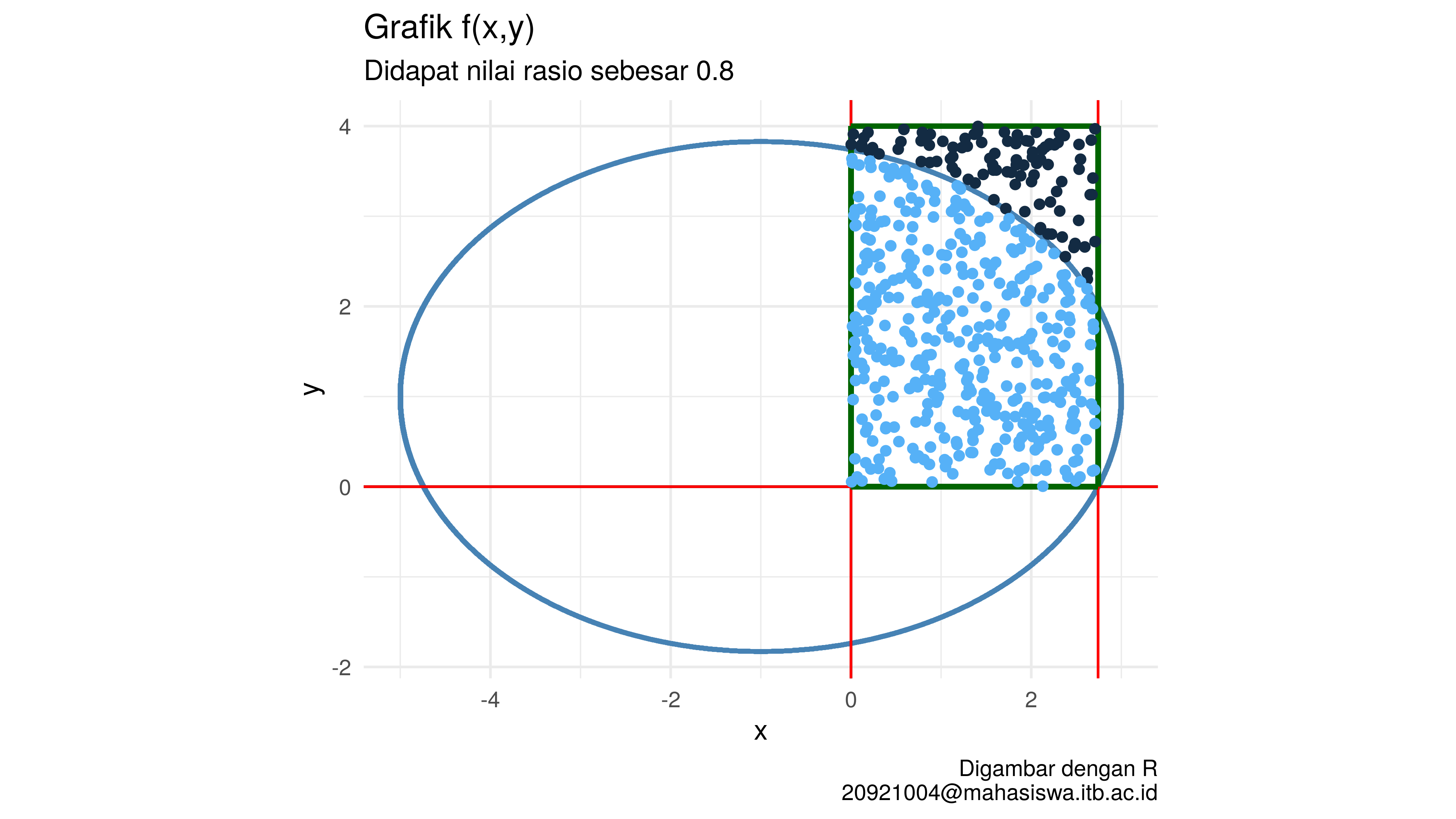
$`Luas area di bawah kurva`
[1] 8.77330364

$`Absolute selisih dg solusi eksak`
[1] 0.117934598

Masalah pada Brute Force Salah satu prinsip metode ini adalah random bumber generator. Oleh karena itu, bisa jadi pada N besar hasilnya tidak lebih baik pada N kecil dalam sekali run.

Untuk mengatasi hal tersebut kita harus melakukan run berulang-ulang dan menghitung nilai rata-ratanya sebagai output finalnya. Saya akan coba melakukan pengulangan sebanyak 100 kali setiap kali run untuk mendapatkan aproksimasi yang lebih baik.

Berikut adalah modifikasi program sebelumnya yang saya berikan nama luasmc.

luas_mc = function(f,x1,x2,y1,y2,N){
  # membuat template vector luas
  luas = c()
  # lakukan 100 x pengulangan
  for(ikanx in 1:100){
    # generating random number
    x = runif(N,x1,x2)
    y = runif(N,y1,y2)
  
    # pengecekan y <= f(x)
    rekap = 
      data.frame(x,y) %>% 
      rowwise() %>% 
      mutate(f_x = f(x),
             on_target = ifelse(y <= f_x,1,0)) %>% 
      ungroup()
  
    # hitung rasio on target vs all dots
    rasio = sum(rekap$on_target) / N
    # hitung luas
    luas_temp = (x2-x1)*(y2-y1)*rasio
    # memasukkan ke dalam template
    luas = c(luas,luas_temp)
  }
  
  # menghitung rata-rata luas
  return(mean(luas))
}

Kita akan coba hitung untuk nilai N yang berbeda-beda sebagai berikut:

n banyak titik Luas aproksimasi Absolute selisih dengan eksak
10 8.71847049 0.063101450
50 8.68776393 0.032394887
100 8.64609073 0.009278305
200 8.67953895 0.024169915
500 8.68140328 0.026034242
1000 8.63282111 0.022547927
2500 8.65824176 0.002872720

Hasil Perhitungan Luas Monte Carlo

Kita bisa lihat bahwa ada indikasi semakin tinggi N yag digunakan, nilai absolut selisih aproksiasi dengan eksak relatif semakin kecil.

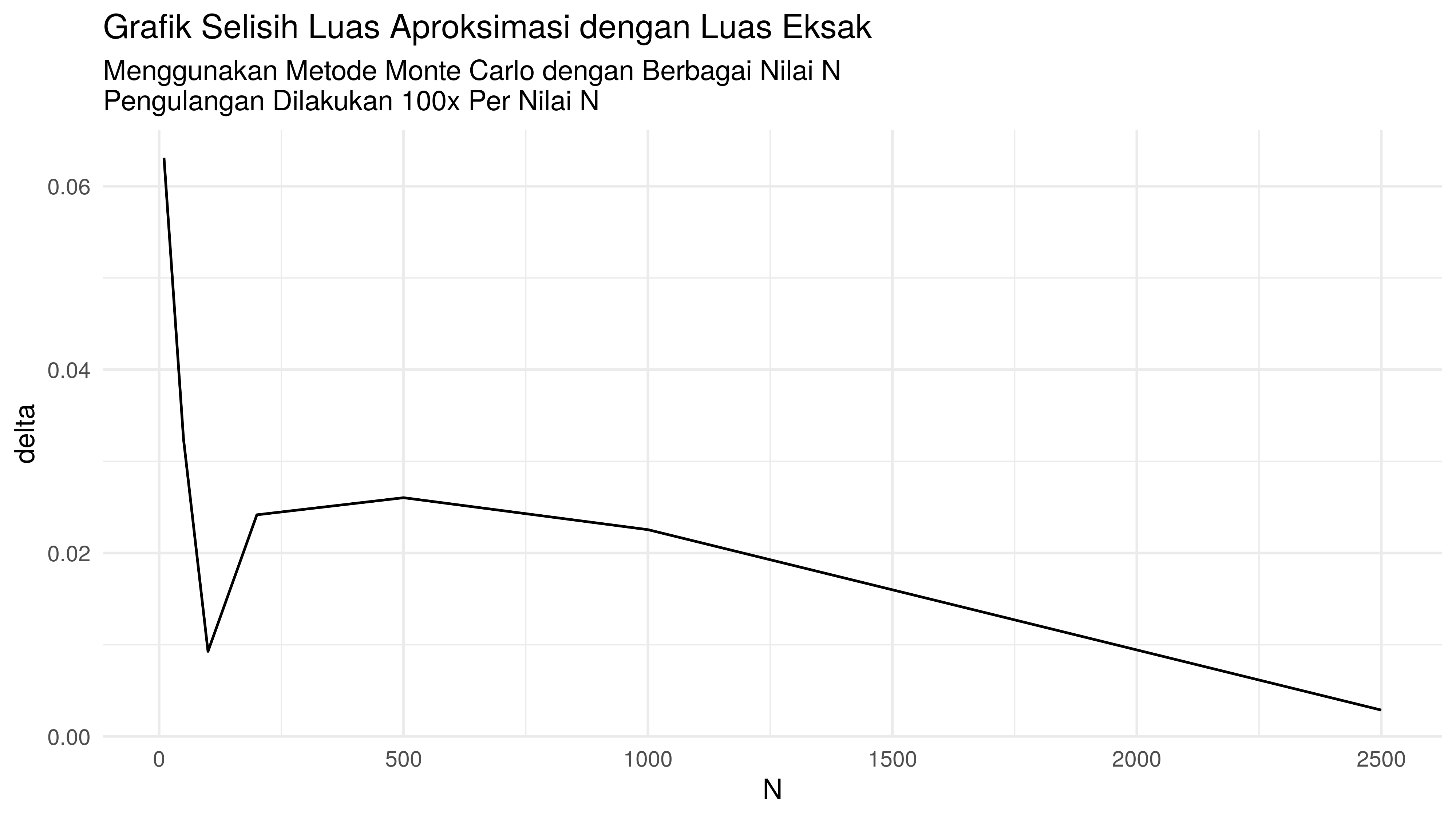
Namun agar metode ini lebih stabil dan konvergen, kita bisa mengulang komputasi lebih banyak per nilai N dengan konsekuensi runtime yang semakin panjang. Pada soal ini, saya menggunakan 100 x pengulangan.

if you find this article helpful, support this blog by clicking the ads.

You May Also Enjoy

Geocoding di R Menggunakan tidygeocoder

7 minute read

Di blog ini saya sudah menuliskan berbagai macam metode dan teknik pengambilan data longlat dari alamat (vice versa). Istilah kerennya itu geocoding.