Tugas/Ujian Sains Komputasi: Algoritma dan Perancangan Software - Tugas III

17 minute read

TASK 1
- Soal
- Jawab
  - Analitik
  - Numerik

TASK 1

Soal

Buatlah algoritma sederhana dengan metode Monte Carlo untuk mencari solusi dari integral berikut:

$f(x) = \int_1^5 x^2 dx$

Bandingkan nilainya jika integralnya dipecah menjadi dua sebagai berikut:

$f(x) = \int_1^3 x^2 dx + \int_3^5 x^2 dx$

Bandingkan dengan solusi analitiknya!

Jawab

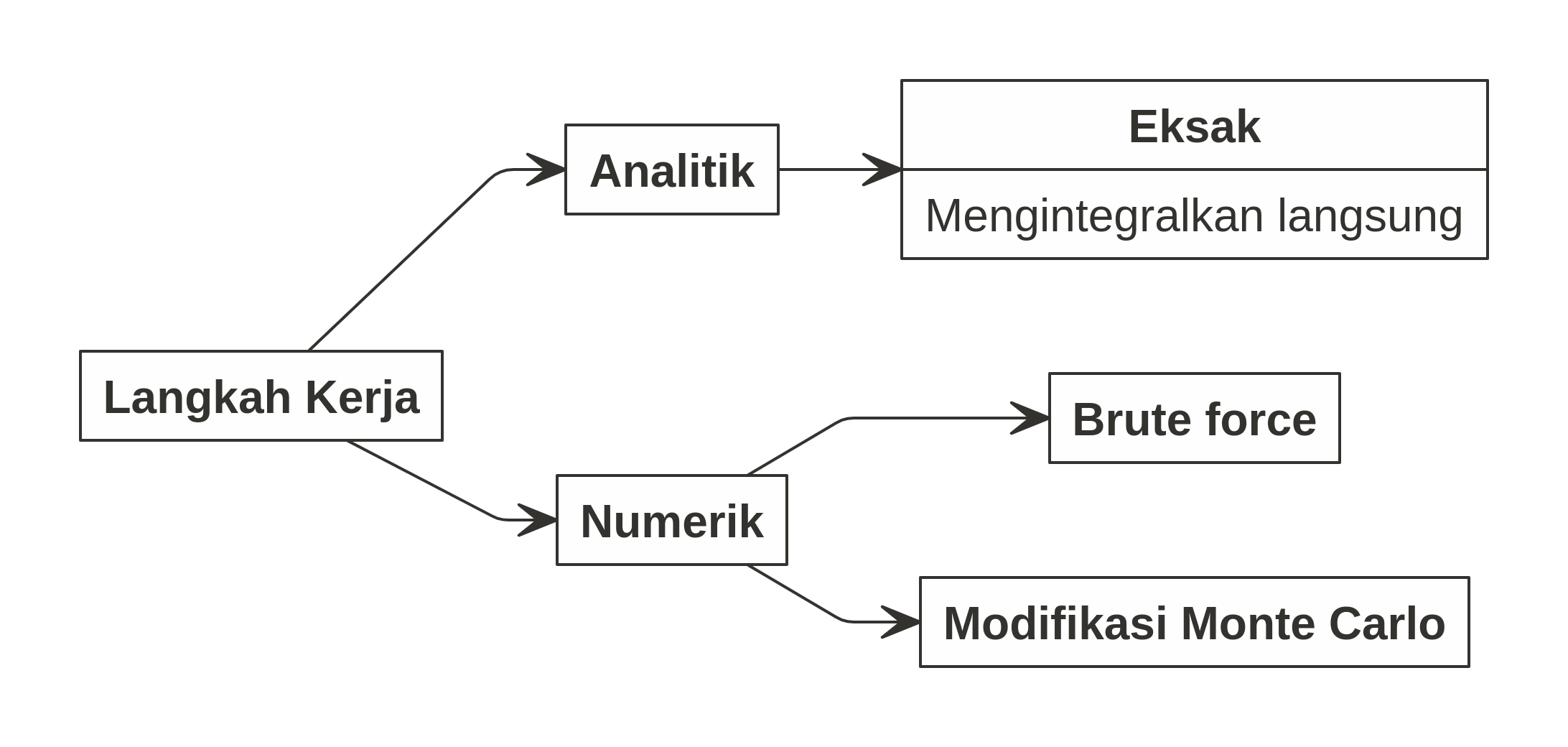
Berikut adalah langkah kerja yang dilakukan untuk menjawab soal ini:

Kelak akan kita bandingkan metode numerik dengan hasil eksaknya.

Analitik

Perhatikan bahwa pada integral tentu berlaku:

$\int_a^b f(x) dx = F(b) - F(a)$

Oleh karena itu, jika kita memiliki $f(x) = x^2$ , maka $F(x) = \int f(x) dx = \frac{x^3}{3}$ dari soal:

$\int_1^5 x^2 dx = \frac{5^3}{3} - \frac{1^3}{3} \approx 41.33333$

Numerik

Brute Force

Analogi dari metode numerik ini adalah seperti melempar darts. Luas area di bawah kurva bisa didefinisikan sebagai:

$L = \frac{N darts_{ \text{on target} }} {N darts_{ \text{All} }}$

Berikut adalah flowchart-nya:

Hal terpenting dalam metode ini adalah mendefinisikan batas titik $x,y$ untuk di-random. Kenapa?

Kita tidak ingin darts yang kita lempar jatuh ke area sembarang! Kita harus definisikan di mana area bermain darts.

Perhatikan grafik $f(x)$ berikut:

Untuk sumbu $x$ , batas titik yang akan di-random sudah jelas, yakni: $[1,5]$ .

Lantas bagaimana dengan sumbu $y$ ?

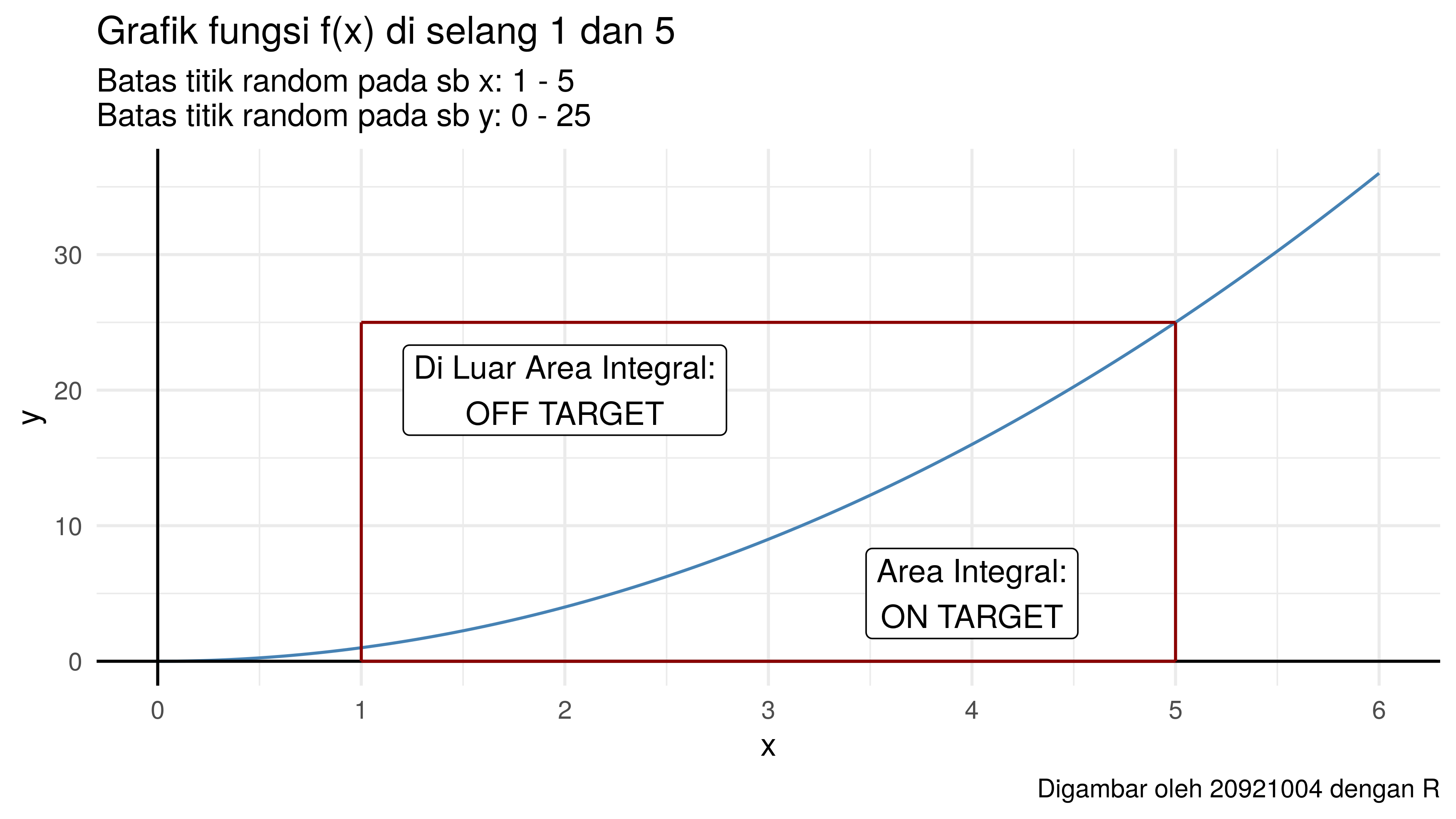
Kita akan membuat sejumlah random di dalam area kotak merah dari grafik di atas. Kelak luas akan dihitung dari rasio titik di dalam area on target dengan total semua titik yang ada dikalikan dengan luas dari kotak merah.

$L = 4 \times 25 \times \frac{N darts_{ \text{on target} }} {N darts_{ \text{All} }}$

Berikut adalah algoritmanya dalam R:

set.seed(2021)

brute_force = function(f,x1,x2,y1,y2,N){
  # generating random number
  x = runif(N,x1,x2)
  y = runif(N,y1,y2)
  
  # pengecekan y <= f(x)
  rekap = 
    data.frame(x,y) %>% 
    mutate(f_x = f(x),
           on_target = ifelse(y <= f_x,1,0))
  
  # hitung rasio on target vs all dots
  rasio = sum(rekap$on_target) / N
  # hitung luas
  luas = (x2-x1)*(y2-y1)*rasio
  
  # perbandingan dengan eksak
  eksak = ((5^3)/3) - 1/3
  delta = abs(eksak - luas)
  
  # output plot
  plot_sim = 
    plot +
    geom_point(data = rekap,aes(x,y,color = on_target)) +
    theme(legend.position = "none") +
    labs(title = paste0("Hasil Simulasi dengan ",N," titik"),
         subtitle = paste0("Didapat nilai rasio sebesar ",rasio))
  
  # output
  output = list(
    "Plot Brute Force" = plot_sim,
    "Luas area di bawah kurva" = luas,
    "Absolute selisih dg solusi eksak" = delta
    )
  
  return(output)
}

Saya menghitung error atau selisih solusi numerik dengan solusi eksak dengan cara:

![\Delta = |eksak - numerik|](https://latex.codecogs.com/svg.latex?%5CDelta%20%3D%20%7Ceksak%20-%20numerik%7C “\Delta =

eksak - numerik

”)

Dari function di atas, kita akan coba hitung dengan berbagai nilai $N$ sebagai berikut:

$N=10$

brute_force(f,x1 = 1,x2 = 5,y1 = 0,y2 = 25,N = 10)

$`Plot Brute Force`

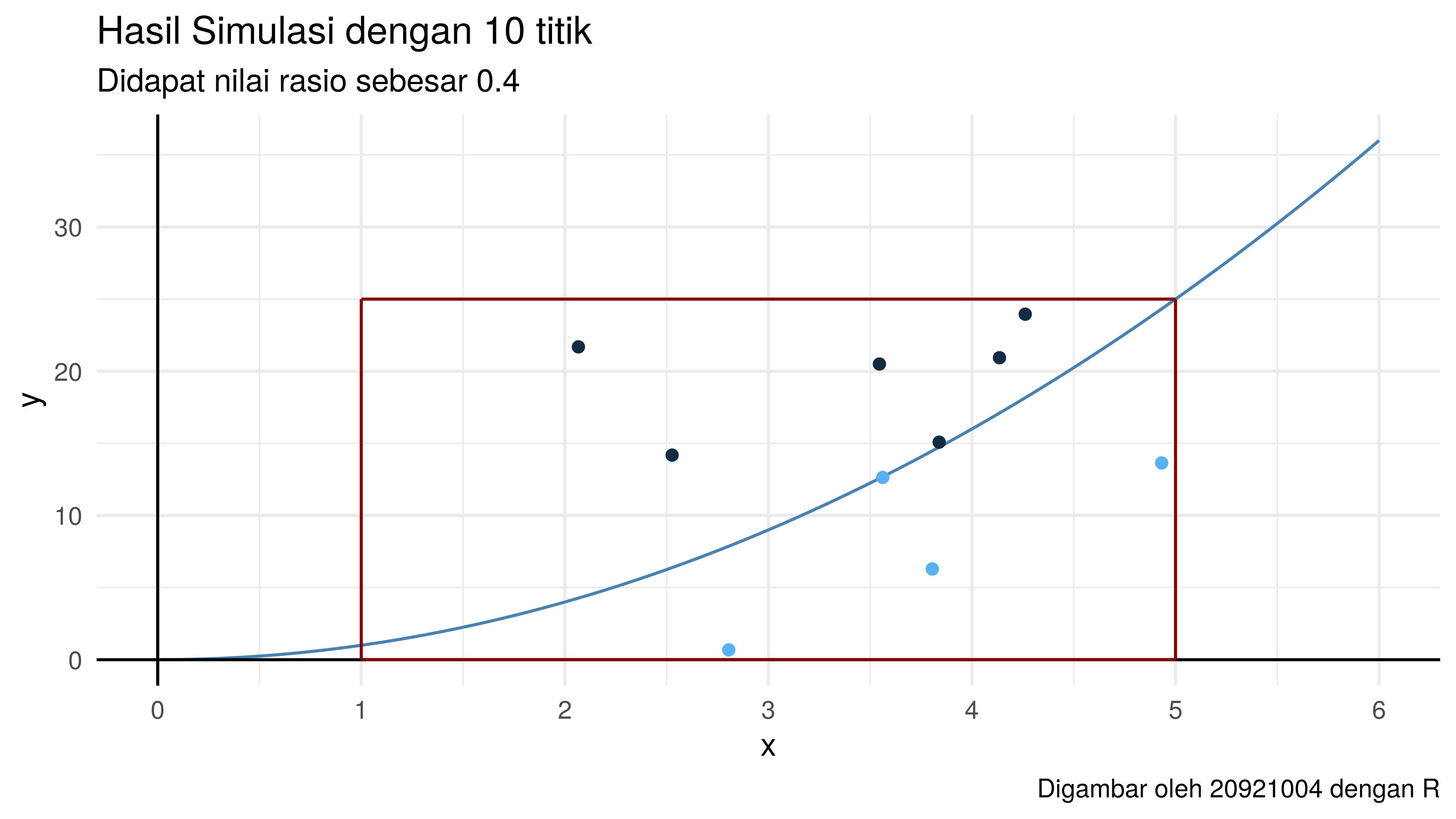
$`Luas area di bawah kurva`
[1] 40

$`Absolute selisih dg solusi eksak`
[1] 1.333333

$N=50$

brute_force(f,x1 = 1,x2 = 5,y1 = 0,y2 = 25,N = 50)

$`Plot Brute Force`

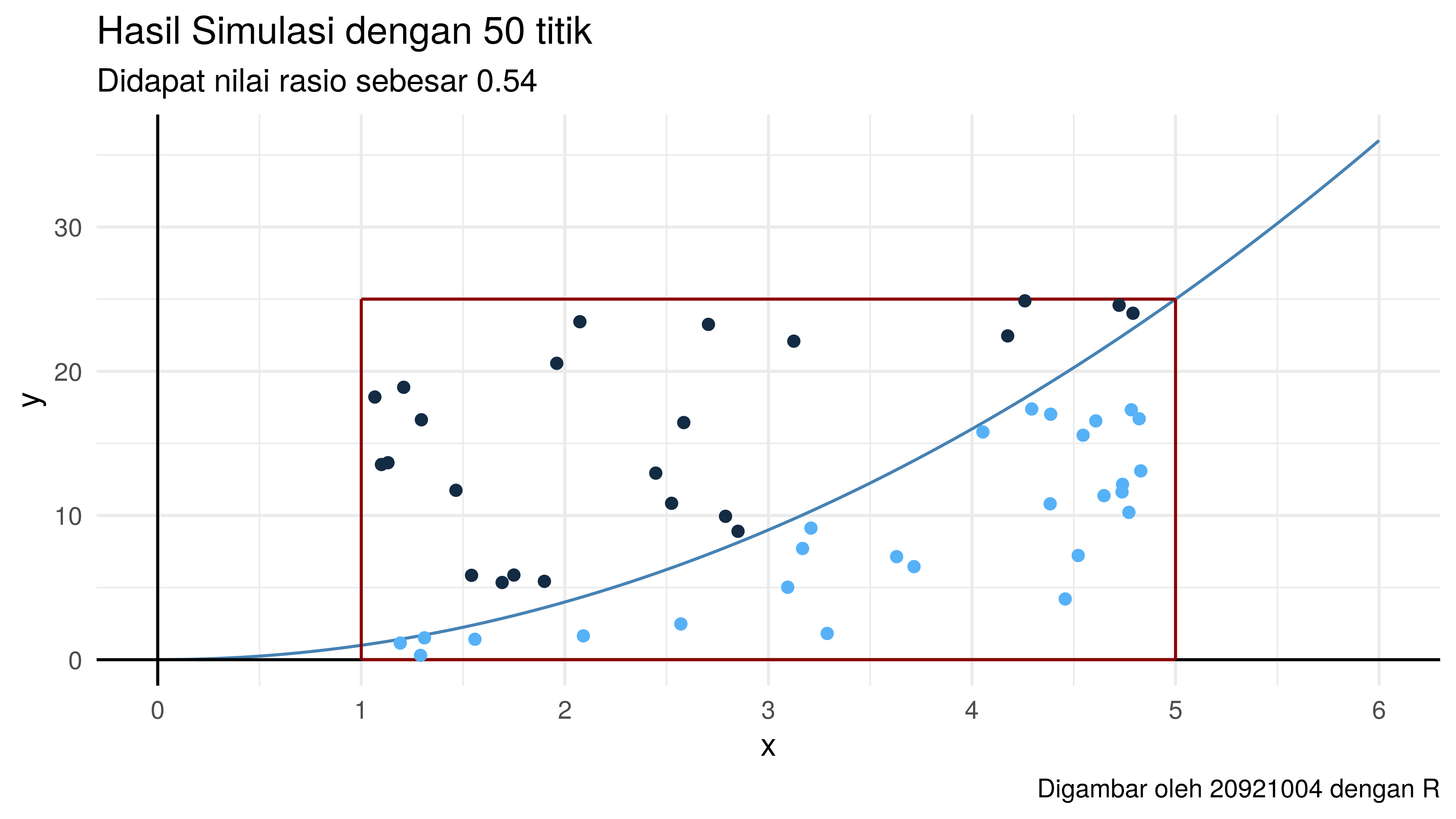
$`Luas area di bawah kurva`
[1] 54

$`Absolute selisih dg solusi eksak`
[1] 12.66667

$N=1000$

brute_force(f,x1 = 1,x2 = 5,y1 = 0,y2 = 25,N = 1000)

$`Plot Brute Force`

$`Luas area di bawah kurva`
[1] 41.6

$`Absolute selisih dg solusi eksak`
[1] 0.2666667

$N=50000$

brute_force(f,x1 = 1,x2 = 5,y1 = 0,y2 = 25,N = 50000)

$`Plot Brute Force`

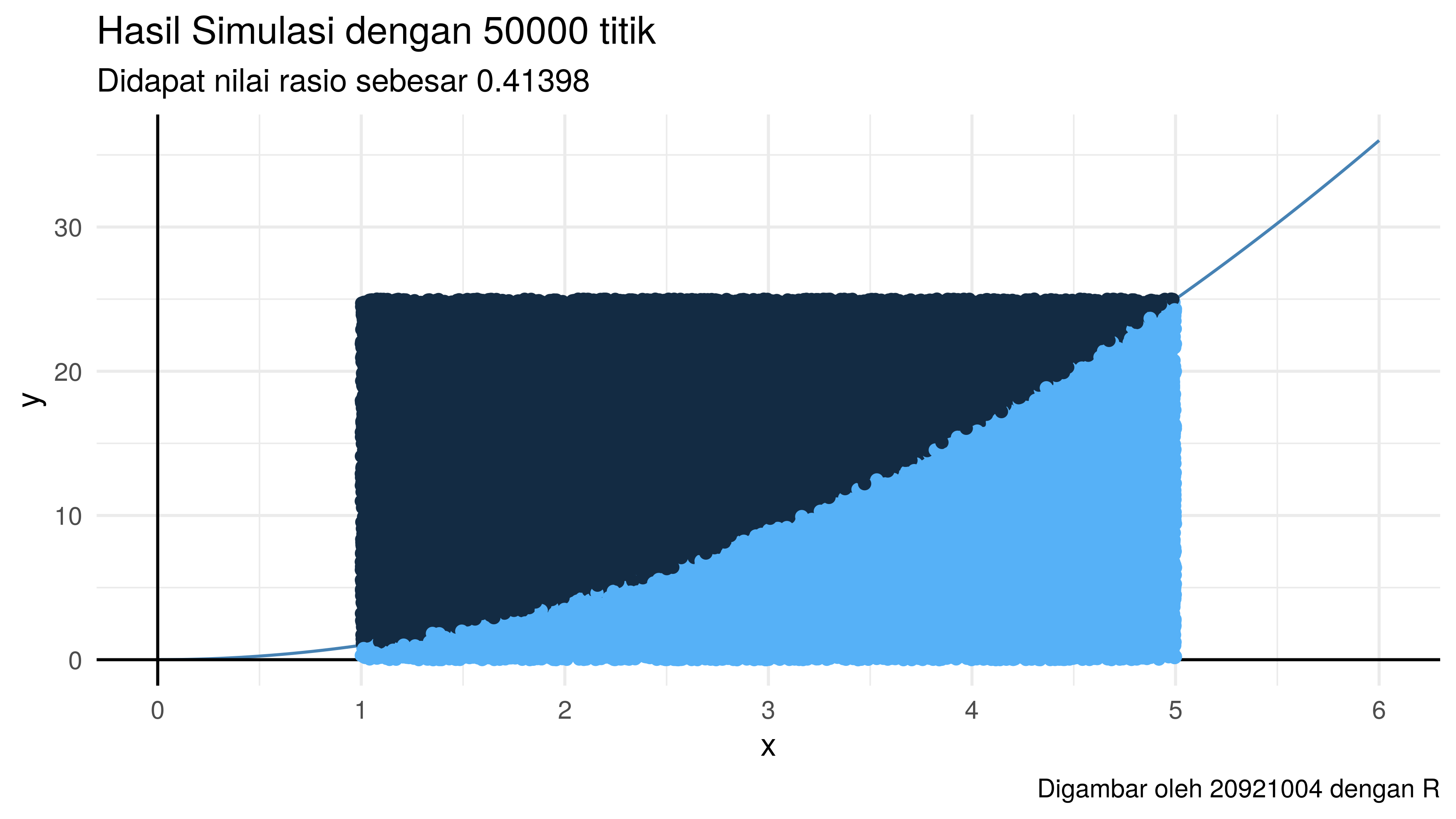
$`Luas area di bawah kurva`
[1] 41.398

$`Absolute selisih dg solusi eksak`
[1] 0.06466667

Bagaimana jika selang integralnya dipisah menjadi:_

$f(x) = \int_1^3 x^2 dx + \int_3^5 x^2 dx$

Menggunakan prinsip yang sama seperti bagian sebelumnya, saya akan buat tabel perbandingan sebagai berikut:

N	Selang 1-5	Selang 1-3 + 3-5	Delta 1-5	Delta 1-3 + 3-5
10	50.00000	55.00000	8.6666667	13.6666667
100	38.00000	35.00000	3.3333333	6.3333333
500	43.60000	41.70000	2.2666667	0.3666667
750	44.53333	41.20000	3.2000000	0.1333333
1000	42.90000	41.40000	1.5666667	0.0666667
5000	42.14000	41.19000	0.8066667	0.1433333
7500	41.73333	41.33333	0.4000000	0.0000000
10000	41.18000	41.82500	0.1533333	0.4916667
25000	40.59200	41.55800	0.7413333	0.2246667
50000	40.89600	41.21400	0.4373333	0.1193333
100000	41.28000	41.25150	0.0533333	0.0818333
250000	41.44920	41.22820	0.1158667	0.1051333
500000	41.37380	41.34020	0.0404667	0.0068667
750000	41.33627	41.33840	0.0029333	0.0050667

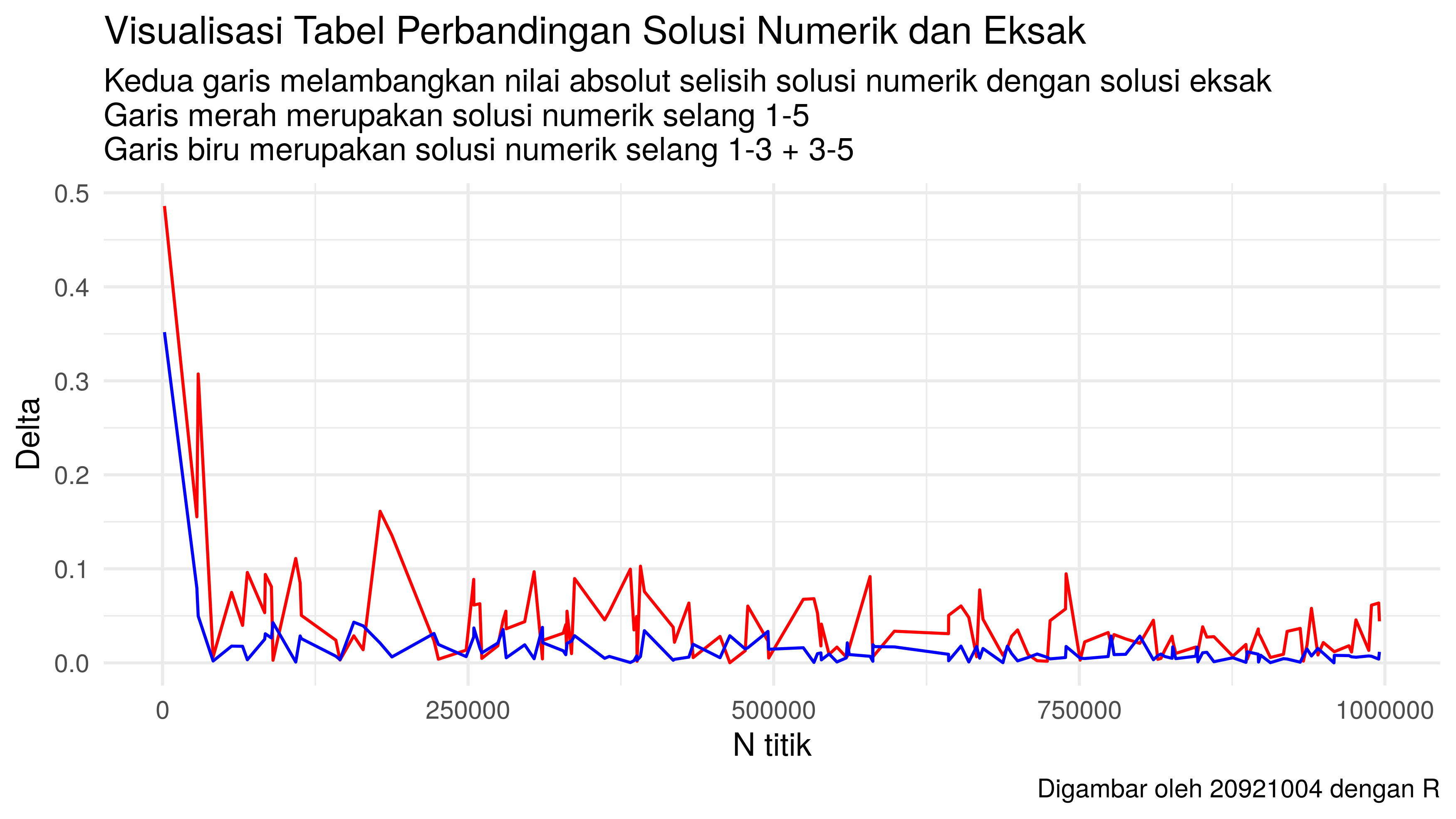
Hasil Perbandingan Solusi Numerik dan Eksak

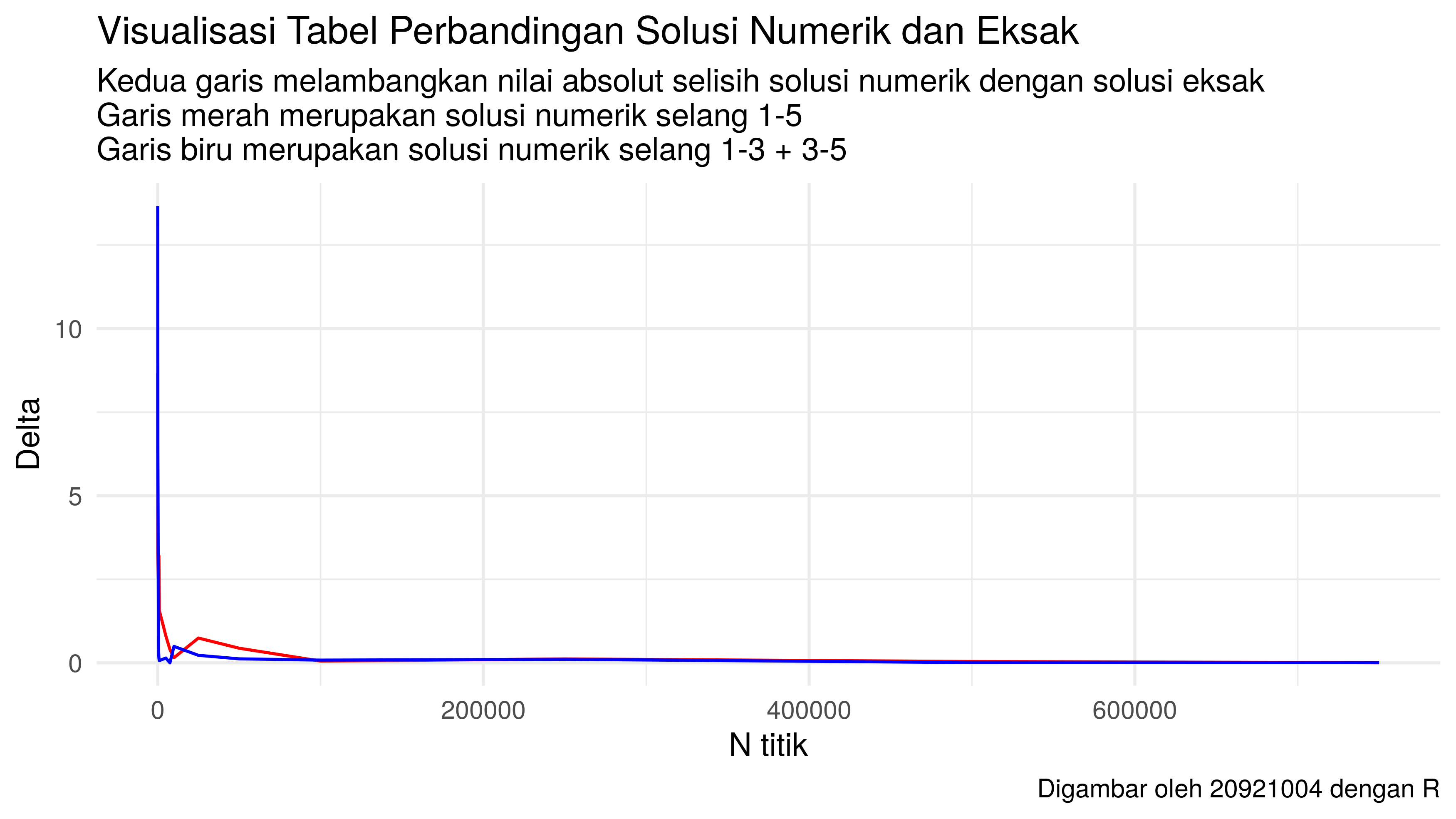
Konklusi Sementara

Secara intuitif, kita bisa melihat bahwa saat selang dibagi menjadi dua, sejatinya kita telah membuat $2 \times$ titik lebih banyak dibanding menggunakan selang awal.

Modifikasi Monte Carlo

Ide dari algoritma ini adalah men-generate titik random di selang integral, kemudian dihitung luas square yang ada.

$I = \int_z^b f(x)dx$

dihitung sebagai:

$<F^N> = \frac{b-a}{N+1} \sum_{i=0}^N f(a + (b-a) \xi_i)$

dengan

$\xi_i \text{ adalah random number antara 0 dan 1}$

Berikut adalah flowchart-nya:

Berdasarkan flowchart di atas, berikut adalah function di R -nya:

modif_monte = function(f,x1,x2,N){
  # generating random number
  x = runif(N,x1,x2)
  # hitung f(x)
  f_x = f(x)
  # hitung luas
  luas = (x2-x1) * f_x
  # mean luas
  mean_luas = mean(luas)
  # output
  return(mean_luas)
  }

Saya menghitung error atau selisih solusi numerik dengan solusi eksak dengan cara:

![\Delta = |eksak - numerik|](https://latex.codecogs.com/svg.latex?%5CDelta%20%3D%20%7Ceksak%20-%20numerik%7C “\Delta =

eksak - numerik

”)

Dari function di atas, kita akan coba hitung dengan berbagai nilai $N$ sebagai berikut:

N	Selang 1-5	Selang 1-3 + 3-5	Delta 1-5	Delta 1-3 + 3-5
1600	41.81926	41.68512	0.4859241	0.3517865
28100	41.48867	41.41292	0.1553348	0.0795848
29200	41.64061	41.38310	0.3072806	0.0497682
41400	41.32692	41.33135	0.0064157	0.0019800
56500	41.25840	41.31553	0.0749363	0.0178029
65500	41.37319	41.35093	0.0398559	0.0175950
69400	41.42950	41.33001	0.0961617	0.0033213
83600	41.38672	41.30822	0.0533898	0.0251127
84100	41.23927	41.36426	0.0940609	0.0309302
89100	41.25233	41.30688	0.0810023	0.0264573
90400	41.33610	41.29055	0.0027676	0.0427851
109000	41.44435	41.33247	0.1110215	0.0008681
112600	41.41836	41.30473	0.0850310	0.0286035
113600	41.28286	41.35909	0.0504742	0.0257552
141800	41.30924	41.32624	0.0240932	0.0070897
145200	41.33033	41.32992	0.0029987	0.0034161
156500	41.30460	41.29008	0.0287327	0.0432545
164100	41.34728	41.29394	0.0139501	0.0393940
178000	41.17209	41.35439	0.1612409	0.0210549
187700	41.19791	41.32701	0.1354196	0.0063240
222100	41.30986	41.36459	0.0234739	0.0312604
225700	41.33723	41.35290	0.0038949	0.0195692
248400	41.31981	41.32669	0.0135230	0.0066471
254600	41.24452	41.36102	0.0888116	0.0276870
254700	41.39484	41.29624	0.0615084	0.0370975
259600	41.39621	41.34907	0.0628816	0.0157412
261200	41.33808	41.34389	0.0047433	0.0105612
274300	41.31526	41.35442	0.0180697	0.0210847
278600	41.37850	41.29782	0.0451640	0.0355131
280900	41.38828	41.32498	0.0549446	0.0083487
281200	41.29711	41.33874	0.0362280	0.0054022
296300	41.28953	41.31415	0.0438007	0.0191800
304000	41.23640	41.33775	0.0969283	0.0044140
310800	41.33753	41.29559	0.0041976	0.0377457
311100	41.30933	41.35475	0.0240006	0.0214155
327800	41.30178	41.34617	0.0315539	0.0128355
329900	41.29272	41.32464	0.0406130	0.0086966
330500	41.34844	41.34925	0.0151077	0.0159195
330900	41.38829	41.31256	0.0549541	0.0207726
334600	41.32349	41.31024	0.0098399	0.0230908
337100	41.24367	41.30444	0.0896615	0.0288887
361700	41.28759	41.33816	0.0457453	0.0048260
365500	41.27898	41.34018	0.0543543	0.0068489
382700	41.43299	41.33371	0.0996603	0.0003745
385700	41.36837	41.33567	0.0350415	0.0023407
387900	41.28396	41.34070	0.0493688	0.0073645
388200	41.33162	41.33054	0.0017165	0.0027903
391000	41.43616	41.34005	0.1028259	0.0067184
394200	41.25750	41.36758	0.0758293	0.0342476
417800	41.29549	41.33608	0.0378439	0.0027417
418800	41.35525	41.32958	0.0219162	0.0037554
430600	41.39695	41.33945	0.0636188	0.0061141
434100	41.32773	41.35314	0.0056080	0.0198112
456100	41.36146	41.33882	0.0281315	0.0054871
464100	41.33347	41.36217	0.0001388	0.0288366
476700	41.34621	41.31857	0.0128797	0.0147587
478800	41.27292	41.34939	0.0604100	0.0160550
495300	41.35654	41.36678	0.0232019	0.0334424
495900	41.33847	41.31887	0.0051353	0.0144667
524200	41.40094	41.34941	0.0676098	0.0160797
532900	41.26510	41.33284	0.0682372	0.0004949
535800	41.38628	41.32356	0.0529508	0.0097717
538600	41.35134	41.34391	0.0180074	0.0105729
539000	41.29209	41.33653	0.0412407	0.0031924
545300	41.32430	41.32383	0.0090342	0.0095002
551700	41.31657	41.33429	0.0167605	0.0009611
559300	41.32713	41.33854	0.0062047	0.0052113
560200	41.34030	41.31204	0.0069631	0.0212936
561800	41.31715	41.32450	0.0161865	0.0088334
578800	41.42511	41.34032	0.0917810	0.0069895
581100	41.34072	41.33165	0.0073893	0.0016874
581200	41.33976	41.31413	0.0064231	0.0192075
582600	41.32465	41.35061	0.0086827	0.0172765
598700	41.36701	41.31635	0.0336754	0.0169832
643000	41.36436	41.34244	0.0310272	0.0091095
643100	41.38389	41.33112	0.0505582	0.0022164
653200	41.39389	41.31550	0.0605562	0.0178352
659600	41.38163	41.33235	0.0482993	0.0009799
666000	41.32681	41.35067	0.0065248	0.0173383
668500	41.25570	41.32834	0.0776308	0.0049914
671200	41.28690	41.34859	0.0464369	0.0152569
687500	41.34136	41.33311	0.0080292	0.0002279
691100	41.34887	41.31559	0.0155340	0.0177480
694600	41.30500	41.34324	0.0283290	0.0099056
699500	41.29834	41.33545	0.0349977	0.0021141
708100	41.34219	41.33901	0.0088584	0.0056784
715500	41.33108	41.34276	0.0022525	0.0094249
723800	41.33161	41.32749	0.0017205	0.0058403
726100	41.37821	41.33758	0.0448813	0.0042443
738700	41.39065	41.32767	0.0573136	0.0056678
739200	41.23861	41.35076	0.0947277	0.0174273
750700	41.33619	41.32840	0.0028596	0.0049383
754400	41.31103	41.32873	0.0222990	0.0046078
773600	41.36559	41.34008	0.0322578	0.0067452
776000	41.35383	41.36183	0.0204966	0.0284997
778400	41.30326	41.34211	0.0300742	0.0087721
787900	41.35883	41.34242	0.0254943	0.0090883
799500	41.31258	41.36175	0.0207540	0.0284153
810600	41.37866	41.33668	0.0453274	0.0033494
814200	41.33709	41.32563	0.0037592	0.0077037
816800	41.33808	41.32394	0.0047490	0.0093897
819900	41.34675	41.34010	0.0134204	0.0067706
825900	41.30501	41.33818	0.0283190	0.0048501
826400	41.30971	41.35032	0.0236247	0.0169880
828900	41.34339	41.32886	0.0100572	0.0044730
845200	41.35013	41.32628	0.0167949	0.0070491
846400	41.32447	41.31664	0.0088587	0.0166923
847000	41.34560	41.33438	0.0122635	0.0010515
850900	41.37169	41.32258	0.0383573	0.0107543
854300	41.36072	41.34455	0.0273883	0.0112214
860100	41.36120	41.33456	0.0278684	0.0012286
875600	41.34042	41.33874	0.0070851	0.0054112
886300	41.35290	41.33387	0.0195643	0.0005365
887400	41.32935	41.34513	0.0039832	0.0117991
896400	41.36939	41.34253	0.0360607	0.0091972
896600	41.30186	41.33245	0.0314742	0.0008879
898400	41.30605	41.32525	0.0272795	0.0080795
906300	41.32763	41.33357	0.0057000	0.0002380
917000	41.34246	41.33777	0.0091285	0.0044345
920000	41.29987	41.33742	0.0334678	0.0040871
930700	41.36998	41.33259	0.0366419	0.0007389
933300	41.33147	41.32566	0.0018610	0.0076756
936300	41.31416	41.34805	0.0191687	0.0147201
939900	41.27535	41.32598	0.0579801	0.0073521
945200	41.34172	41.31805	0.0083860	0.0152811
949600	41.31171	41.34355	0.0216260	0.0102158
958300	41.32117	41.33336	0.0121623	0.0000283
958600	41.32149	41.32537	0.0118480	0.0079589
970500	41.31517	41.34104	0.0181645	0.0077070
972700	41.34482	41.32690	0.0114848	0.0064341
976300	41.28765	41.33933	0.0456865	0.0059945
986800	41.34657	41.32598	0.0132404	0.0073556
989000	41.39467	41.32631	0.0613390	0.0070265
994900	41.39698	41.33734	0.0636470	0.0040077
995500	41.37752	41.32160	0.0441827	0.0117368

Hasil Perbandingan Solusi Numerik dan Eksak

Share on

Twitter Facebook LinkedIn

Bunch of Ideas, a little bit of Maths.

Tugas/Ujian Sains Komputasi: Algoritma dan Perancangan Software - Tugas III

TASK 1

Soal

Jawab

Analitik

Numerik

Brute Force

Konklusi Sementara

Modifikasi Monte Carlo

Share on

You May Also Enjoy

Menghitung Jarak Antara Dua Lokasi di R Menggunakan OSRM

Geocoding di R Menggunakan tidygeocoder

Apa Saja Komen Netizen di Post Instagram Terhits Nutrifood Sepanjang Tahun 2024

Pengelompokkan Data Teks Menggunakan LLM Word Embedding dan Hierarchical Clustering