Mengenal Analisa Bayesian yang Hasilnya Lebih Holistik

Sudah beberapa tahun ini saya sering mendengar istilah Bayesian berseliweran di berbagai artikel. Konon, statistika yang selama ini dipelajari oleh kita semua itu termasuk ke dalam frequentist. Bayesian ini bisa mengubah cara pandang kita terhadap statistik karena memiliki perubahan cara pandang terhadap pengambilan keputusannya.

Bayesian adalah filosofi dan metodologi dalam statistika yang dinamai dari Teorema Bayes (ditemukan oleh Thomas Bayes). Inti dari pendekatan ini adalah memperbarui keyakinan kita tentang suatu hal berdasarkan bukti atau data baru.

Bayangkan kita memiliki sebuah hipotesis atau asumsi awal (disebut dengan Prior). Ketika data baru datang, kita menggunakan data tersebut untuk memperbarui keyakinan awal (hasil pembaruannya disebut Posterior).

1. Prior: Keyakinan awal kita tentang suatu parameter (misalnya, rata-rata tinggi badan) sebelum melihat data. Ini bisa berdasarkan pengetahuan ahli, penelitian sebelumnya, atau asumsi yang masuk akal.
2. Likelihood: Probabilitas untuk mengamati data yang kita miliki jika hipotesis kita benar. Ini mirip dengan konsep dalam statistika frequestist.
3. Posterior: Keyakinan yang telah diperbarui tentang parameter tersebut setelah kita menggabungkan keyakinan awal (Prior) dengan bukti dari data baru (Likelihood). Ini adalah hasil akhir yang kita cari.

Analogi Bayesian itu seperti:

1. Memasak dengan resep (prior = bumbu dasar).
2. Mencicipi terus (data baru).
3. Menyesuaikan rasa (posterior = resep yang disesuaikan).

Contoh Sederhana: Mendiagnosa Penyakit

Misalkan secara umum kita mengetahui bahwa ada suatu penyakit langka yang hanya diderita oleh 1% populasi.

Ini adalah keyakinan awal (prior).

Kemudian ada seseorang pasien yang hendak dites untuk mengetahui apakah pasien tersebut mengidap penyakit langka atau tidak. Suatu tes digunakan dengan akurasi 99% (baik untuk orang sakit maupun sehat). Ternyata hasil tes tersebut menyatakan positif.

Bagi frequentist, probabilitas seseorang tersebut mengidap penyakit adalah sebesar 99%.

Namun bagi Bayesian, probabilitas seseorang tersebut mengidap penyakit adalah sebesar 50%. Lho kok bisa? Kenapa bukan 99%? Pada kasus ini Bayesian menggunakan confusion matrix untuk menghitung peluang bersyarat seorang pasien sakit jika hasil tesnya positif. Intuisi di balik hasil ini:

1. Penyakit sangat langka (hanya 1% populasi)
2. Meskipun tes sangat akurat (99%), false positive-nya 1%.
3. Karena populasi sehat sangat besar (99%), jumlah false positive menjadi signifikan

Begini perhitungannya:

Dari informasi yang ada pada, kita bisa definisikan:

1. : Probabilitas sakit = 1% = 0.01.

2. 

   Probabilitas tes positif jika pasien sakit = 99% = 0.99.

3. 

   Probabilitas tes negatif jika pasien sehat = 99% = 0.99.

Kita ingin mencari: , yakni probabilitas pasien sakit jika tes positif.

# Probabilitas prior
P_S              = 0.01  # Probabilitas sakit
P_Tplus_given_S  = 0.99  # Probabilitas tes positif jika sakit
P_Tminus_given_H = 0.99  # Probabilitas tes negatif jika sehat

# Probabilitas sehat
P_H = 1 - P_S  # 0.99

# Probabilitas tes positif jika sehat (False Positive)
P_Tplus_given_H = 1 - P_Tminus_given_H  # 1 - 0.99 = 0.01

# Probabilitas marginal tes positif
P_Tplus = (P_Tplus_given_S * P_S) + (P_Tplus_given_H * P_H)

# Teorema Bayes: P(S|T+) = [P(T+|S) × P(S)] / P(T+)
P_S_given_Tplus = (P_Tplus_given_S * P_S) / P_Tplus
P_S_given_Tplus

[1] 0.5

Kita dapatkan probabilitasnya sebesar 50%.

Sekarang kita akan lakukan simulasi untuk populasi sebanyak 10.000 orang.

# Analisis dengan populasi 10,000 orang
populasi = 10000

# Jumlah yang sakit dan sehat
sakit = populasi * P_S      
sehat = populasi * P_H      

# Tes positif pada orang sakit (True Positive)
TP <- sakit * P_Tplus_given_S 

# Tes positif pada orang sehat (False Positive)
FP <- sehat * P_Tplus_given_H  

# Total tes positif
total_positif <- TP + FP

# Probabilitas sakit jika tes positif
prob_sakit_jika_positif <- TP / total_positif

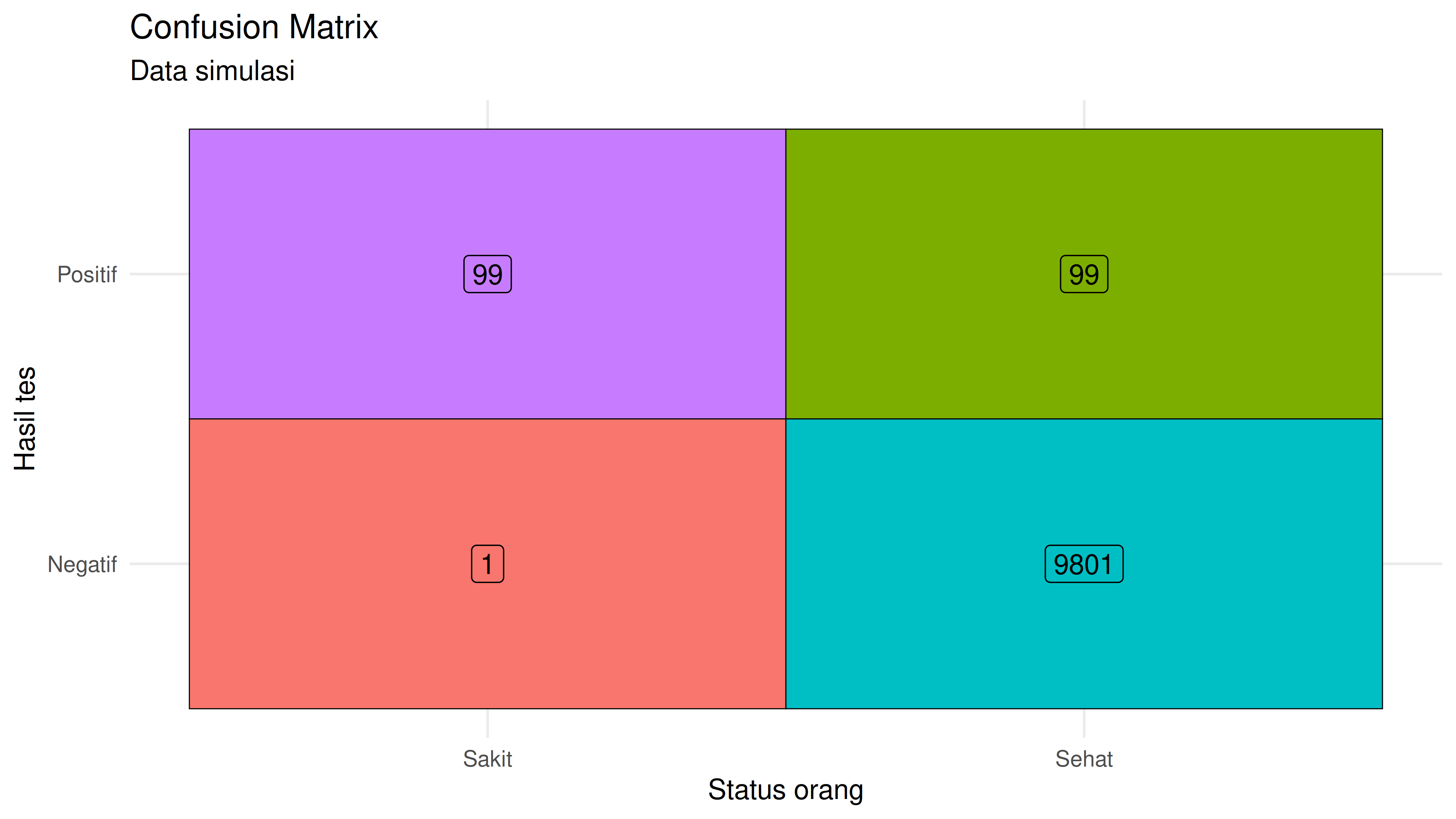
Analisis Populasi 10.000 orang:

Jumlah sakit: 100 orang

Jumlah sehat: 9900 orang

True Positive (sakit dan tes positif): 99 orang

False Positive (sehat tapi tes positif): 99 orang

Total tes positif: 198 orang

Probabilitas sakit jika tes positif: 0.5 = 50 %

Kesimpulan Penting

1. Bayesian mempertimbangkan base rate (prevalensi penyakit).
2. Untuk penyakit langka, bahkan tes yang sangat akurat bisa menghasilkan banyak false positive.
3. Hasil tes harus diinterpretasi dalam konteks prevalensi.
4. Inilah mengapa tes diagnostik sering dikonfirmasi dengan tes kedua.

Bagaimana? Cukup membingungkan ya? Hehe. Sama!

Awalnya mungkin kita belum terbiasa dengan proses logikanya. Sekarang saya akan berikan contoh kasus lain yang relevan dengan bisnis, yakni kasus A/B Testing.

Contoh Lainnya: A/B Testing

A/B testing adalah sebuah metode eksperimen yang sangat sederhana untuk membandingkan dua versi dari sesuatu. Misalnya dua judul email, dua desain iklan, atau dua tata letak halaman web. Tujuannya adalah untuk melihat mana yang memberikan hasil lebih baik.

Misalkan kita memiliki dua ide dan ingin tahu mana yang paling disukai oleh audiens. Alih-alih menebak, kita membagi audiens menjadi dua kelompok secara acak. Kelompok A melihat ide pertama dan Kelompok B melihat ide kedua. Dengan mengukur respons dari masing-masing kelompok, seperti berapa banyak yang mengklik tautan atau melakukan pembelian, kita bisa mendapatkan bukti nyata tentang versi mana yang lebih efektif dalam mencapai tujuan Anda.

Frequentist akan memastikan bahwa perbedaan hasil yang Anda lihat antara Versi A dan Versi B bukanlah karena kebetulan semata. Metode yang digunakan adalah konsep signifikansi statistik untuk memberikan keyakinan bahwa jika Anda memilih versi pemenang, keputusan tersebut didasarkan pada data yang kuat, bukan keberuntungan acak.

Dalam A/B testing Bayesian, kita tidak hanya melihat mana yang lebih baik tetapi seberapa yakin kita bahwa B lebih baik daripada A (vice versa) dan berapa besar perkiraan improvement-nya.

Mulai bingung ya? Oke, saya coba simulasikan contoh A/B testing sederhana ya. Misalkan ada dua buah marketing campaigns (A dan B) yang diuji coba selama 30 hari kepada dua kelompok dalam suatu target market. Sudah dipastikan bahwa tidak ada orang yang melihat kedua marketing campaigns tersebut (hanya salah satu saja).

nama	hari	pengunjung	konversi
Campaign A	1	100	2
Campaign A	2	100	4
Campaign A	3	100	2
Campaign A	4	100	5
Campaign A	5	100	6
Campaign A	6	100	0
Campaign A	7	100	3
Campaign A	8	100	5
Campaign A	9	100	3
Campaign A	10	100	3
Campaign A	11	100	6
Campaign A	12	100	3
Campaign A	13	100	4
Campaign A	14	100	3
Campaign A	15	100	1
Campaign A	16	100	5
Campaign A	17	100	2
Campaign A	18	100	0
Campaign A	19	100	2
Campaign A	20	100	6
Campaign A	21	100	5
Campaign A	22	100	4
Campaign A	23	100	3
Campaign A	24	100	8
Campaign A	25	100	4
Campaign A	26	100	4
Campaign A	27	100	3
Campaign A	28	100	3
Campaign A	29	100	2
Campaign A	30	100	1

nama	hari	pengunjung	konversi
Campaign B	1	100	8
Campaign B	2	100	7
Campaign B	3	100	5
Campaign B	4	100	6
Campaign B	5	100	1
Campaign B	6	100	4
Campaign B	7	100	6
Campaign B	8	100	3
Campaign B	9	100	3
Campaign B	10	100	3
Campaign B	11	100	2
Campaign B	12	100	4
Campaign B	13	100	4
Campaign B	14	100	4
Campaign B	15	100	2
Campaign B	16	100	2
Campaign B	17	100	3
Campaign B	18	100	4
Campaign B	19	100	3
Campaign B	20	100	7
Campaign B	21	100	1
Campaign B	22	100	4
Campaign B	23	100	6
Campaign B	24	100	2
Campaign B	25	100	5
Campaign B	26	100	3
Campaign B	27	100	2
Campaign B	28	100	6
Campaign B	29	100	7
Campaign B	30	100	4

Ringkasan Data A/B Test:

Versi A - Total konversi: 102 dari 3000 pengunjung ( 0.034 )

Versi B - Total konversi: 121 dari 3000 pengunjung ( 0.0403 )

Bagi saya yang seorang frequentist, saya biasanya cukup melihat apakah conversion rate campaign B lebih tinggi signifikan dibandingkan campaign A.

Nah, bagaimana cara analisa Bayesian? Kita mulai dengan menentukan prior. Prior bisa ditentukan dengan:

1. Data historikal sebelumnya, atau
2. Dugaan atau hipotesis dari expert, atau
3. Diasumsikan random berdasarkan distribusi beta.

Banyak kasus Bayesian menggunakan distribusi beta untuk menggambarkan distribusi dari posterior. Bagaimana penjelasannya? Analoginya seperti ini:

Bayangkan saya hendak menebak seberapa jago seorang teman bermain basket, khususnya dalam melakukan lemparan bebas. “Jago” di sini adalah sebuah probabilitas (nilai antara 0 sampai 1, atau 0% sampai 100%). Saya belum pernah melihat teman saya bermain, jadi tebakan awal saya mungkin sangat luas.

Di sinilah Distribusi Beta berperan. Anggap saja Distribusi Beta adalah sebuah wadah keyakinan yang fleksibel untuk menampung tebakan saya tentang probabilitas. Wadah ini memiliki dua inputs untuk mengatur bentuknya, yaitu dan .

sebagai jumlah lemparan “masuk” yang sudah saya saksikan (atau saya duga). sebagai jumlah lemparan “gagal” yang sudah saya saksikan (atau saya duga).

Karena saya buta sama sekali terhadap seberapa “jago” teman saya, Anda bisa set dan . Ini membuat wadah keyakinan saya flat, artinya semua kemungkinan (dari 0% jago sampai 100% jago) sama masuk akalnya bagi saya.

Sekarang, teman saya mulai melempar bola. Dia melakukan 10 lemparan, 7 masuk (sukses) dan 3 gagal. Di sinilah keajaiban Bayesian dan Distribusi Beta terjadi. Untuk memperbarui keyakinan saya, prosesnya sangat mudah: Saya cukup menambahkan data baru ke pegangan wadah!

• Alpha baru = lama + lemparan masuk = 1 + 7 = 8
• Beta baru = lama + lemparan gagal = 1 + 3 = 4

Wadah keyakinan saya yang tadinya datar, sekarang bentuknya berubah. Puncaknya bergeser ke arah 8 / (8+4) = 0.67 atau 67%.

Ini adalah keyakinan baru Saya: kemungkinan besar teman saya punya tingkat keberhasilan sekitar 67%.

Oke kita kembali ke kasus A/B Testing awal. Misalkan saya asumsikan prior untuk campaign A dan campaign B sama.

# Prior non-informatif (tidak ada asumsi awal)
# Beta(1,1) = Uniform distribution
alpha_prior = 1
beta_prior  = 1

Kemudian dari data pada kedua tabel di atas, saya akan memperbarui posterior untuk campaign A dan campaign B.

# Hitung posterior parameters
posterior_A = c(
  alpha = alpha_prior + sum(data_A$konversi),
  beta  = beta_prior + (sum(data_A$pengunjung) - sum(data_A$konversi))
)

posterior_B = c(
  alpha = alpha_prior + sum(data_B$konversi),
  beta = beta_prior + (sum(data_B$pengunjung) - sum(data_B$konversi))
)

Parameter Posterior:

Versi A: Beta( 103 , 2899 )

Versi B: Beta( 122 , 2880 )

Setelah itu, saya akan buat density plot dari conversion rate campaign A dan campaign B.

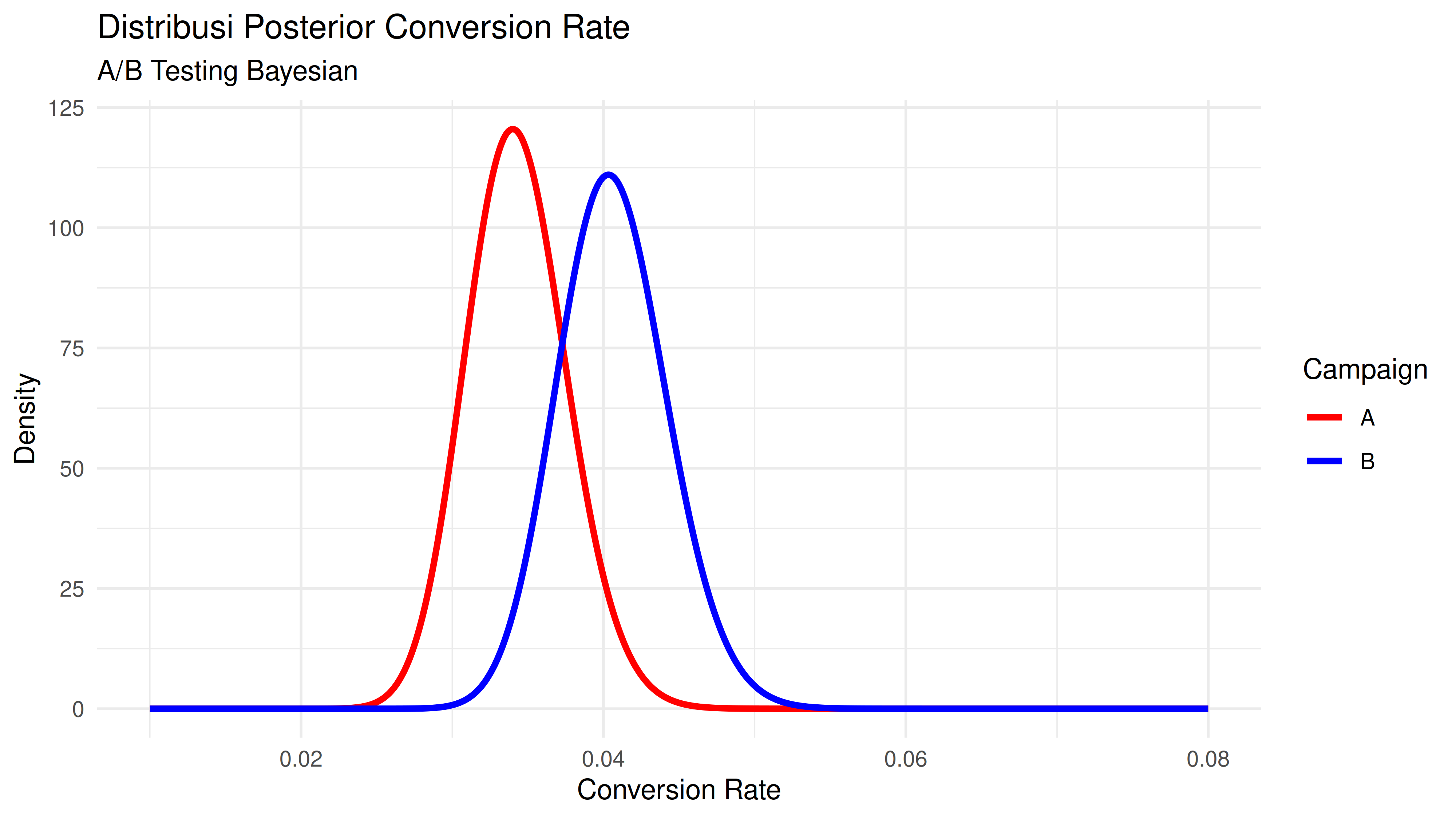
Terlihat dari grafik di atas bahwa secara distribusi, campaign B relatif lebih baik conversion rate-nya. Pertanyaan selanjutnya adalah: seberapa baik campaign B?

Bayesian bisa melakukan analisis perbandingan menggunakan simulasi Monte Carlo. Saya akan coba membuat 100 ribu simulasi dan akan membandingkan berapa banyak kejadian conversion rate campaign B lebih tinggi dibandingkan campaign A.

# Simulasi Monte Carlo
n_simulations = 100000

# Sample dari posterior distributions
samples_A = rbeta(n_simulations, posterior_A["alpha"], posterior_A["beta"])
samples_B = rbeta(n_simulations, posterior_B["alpha"], posterior_B["beta"])

# Probabilitas B > A
prob_B_better = mean(samples_B > samples_A)

# Berapa kali B better
berapa_kali_B = sum(samples_B > samples_A)

Berapa kali kejadian conversion rate campaign B lebih baik daripada conversion rate campaign A: 90054 kali


Probabilitas B lebih baik daripada A: 0.9005 ( 90.05 % )

Selanjutnya kita bisa menghitung lift, yaitu perbedaan conversion rate antara campaign B dan campaign A.

# Hitung lift (improvement)
lift          = (samples_B - samples_A) / samples_A
relative_lift = samples_B - samples_A

# Analisis lift
lift_summary <- data.frame(
  metric = c("Mean Lift", "Median Lift", "95% CI Lower", "95% CI Upper"),
  value = c(
    mean(lift),
    median(lift),
    quantile(lift, 0.025),
    quantile(lift, 0.975)
  )
)

metric	value
Mean Lift	0.1953679
Median Lift	0.1844093
95% CI Lower	-0.0848808
95% CI Upper	0.5377136

Interpretasinya:

1. Mean Lift: 19.54%.
   • Rata-rata peningkatan conversion rate campaign B dibandingkan campaign A.
   • Artinya campaign B secara rata-rata 19.54% lebih baik dari campaign A.
2. Median Lift: 18.44%
   • Nilai tengah dari distribusi lift.
   • Lebih robust terhadap outlier dibanding mean.
3. 95% Credible Interval Lower: -8.49%
   • Batas bawah interval kepercayaan 95%.
   • Dalam skenario terburuk, conversion rate campaign B bisa 8.49% lebih buruk dari conversion rate campaign A.
4. 95% Credible Interval Upper: 53.77%
   • Batas atas interval kepercayaan 95%.
   • Dalam skenario terbaik, conversion rate campaign B bisa 53.77% lebih baik dari conversion rate campaign A.

Berikut adalah density plot dari lift yang sudah saya hitung di atas:

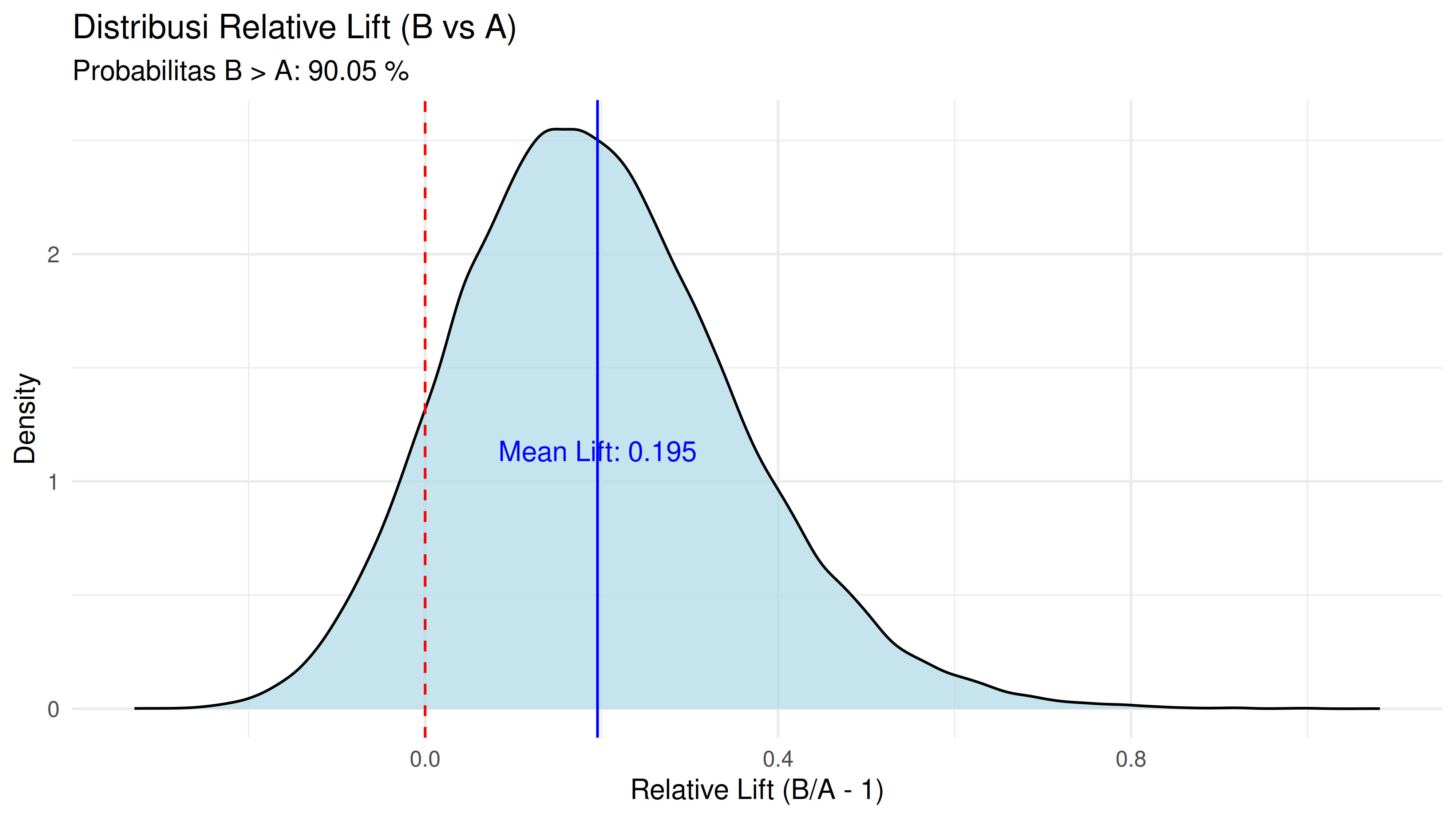
Dari distribusi relative lift di atas, kita bisa melihat bahwa kemungkinan conversion rate campaign B lebih rendah dibandingkan conversion rate campaign A cukup kecil.

Bayesian juga bisa digunakan untuk menghitung expected loss. Apa maksudnya? Kita bisa menghitung loss saat memilih campaign B tapi ternyata campaign A lebih baik conversion rate-nya (vice versa).

# Expected loss jika memilih salah satu versi
expected_loss_A <- mean(pmax(samples_B - samples_A, 0))  # Loss jika pilih A padahal B lebih baik
expected_loss_B <- mean(pmax(samples_A - samples_B, 0))  # Loss jika pilih B padahal A lebih baik

Berikut ini adalah hasil analisanya:

Expected Loss Analysis:

Expected Loss jika pilih A: 0.00655 

Expected Loss jika pilih B: 0.00023 

Kesimpulan: B secara praktis lebih baik (expected loss lebih kecil)

Salah satu keunggulan Bayesian adalah, analisa-analisa di atas bisa dilakukan iteratif harian. Jadi keputusan bisa diambil tanpa harus menunggu 30 hari. Secara bisnis, hal ini sangat berguna untuk meminimalisir budget dari eksperimen. Analisa ini disebut dengan sequential analysis.

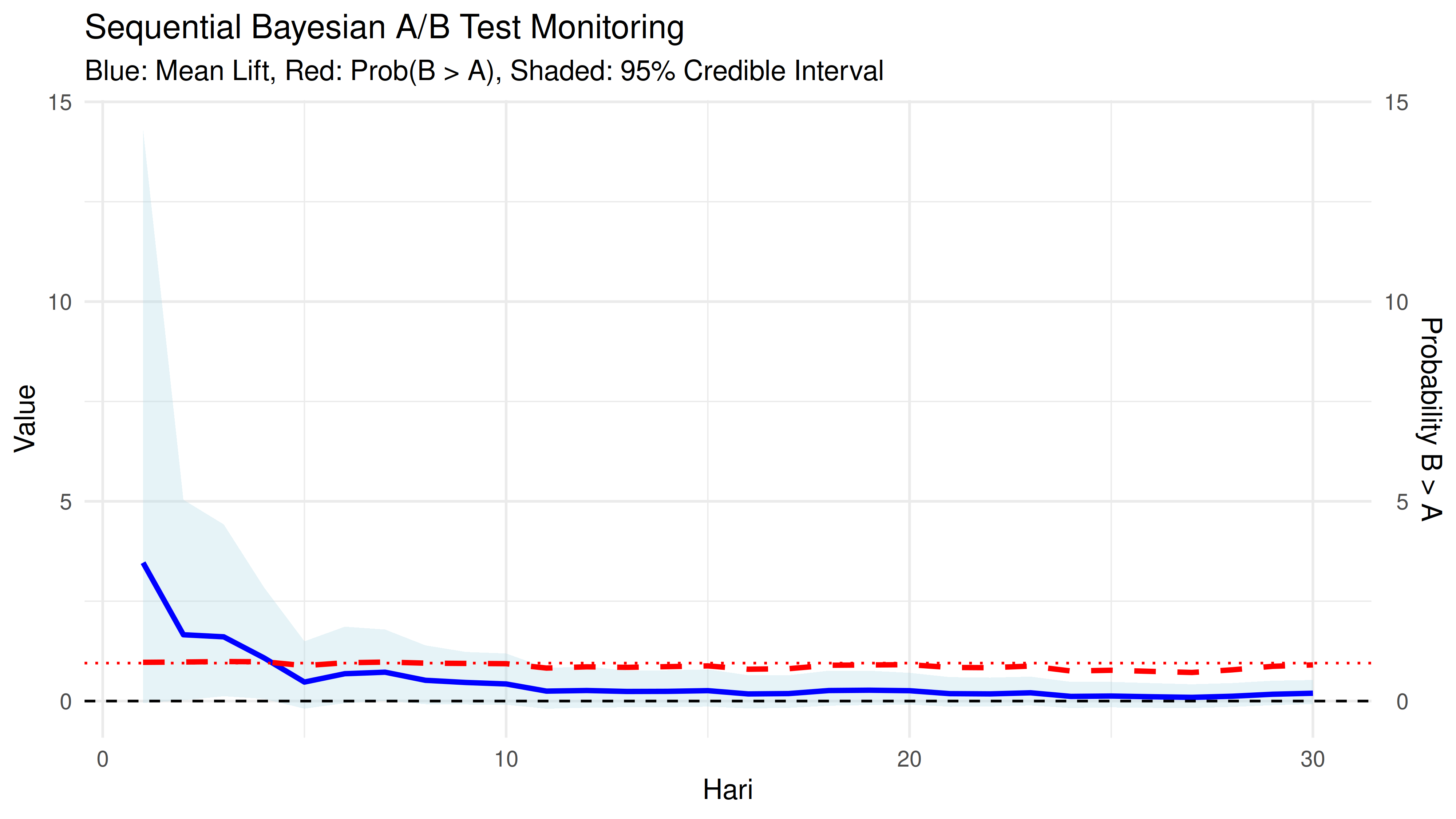
Insights dari grafik di atas adalah:

1. Campaign B konsisten menunjukkan probabilitas tinggi (>85%) untuk lebih baik dari campaign A.
2. Lift tertinggi di awal eksperimen (hari 1-4), kemudian stabil di sekitar 15-25%.
   • Hari 1-4: Lift sangat tinggi (100-345%) dengan interval kredibel lebar.
   • Ini menunjukkan data awal yang tidak stabil.
3. Lift stabil di hari ke 15-30.
   • Lift stabil di 10-25%.
   • Interval kredibel semakin sempit.
   • Probabilitas konsisten di 75-90%.

Catatan untuk eksperimen berikutnya:

• Pertimbangkan menghentikan eksperimen lebih awal (sekitar hari ke 15).
• Data sudah cukup konklusif di tengah eksperimen.
• Hemat waktu dan resources.

---

KESIMPULAN

Bayesian memiliki keuntungan dibandingkan frequentist karena bisa melakukan analisa yang lebih holistik karena melibatkan distribusi dari data simulasi yang ada. Kita juga bisa mengambil keputusan dengan lebih tepat dan cepat tanpa harus menunggu semua prosesnya selesai.

---

if you find this article helpful, support this blog by clicking the ads.