Analisa Bayesian terhadap Tren Persentase Loyal User suatu Brand
Pada tulisan ini saya masih akan membahas tentang Bayesian Statistics untuk menyelesaikan masalah saya di kantor. Tentu saya tidak akan menggunakan data real pada tulisan ini namun saya akan menggunakan data masking yang serupa tapi tak sama. Bagaimana masalah saya? Berikut ini ceritanya:
Setiap tahun, saya dan tim selalu melakukan survey konsumen untuk mencari tahu dari populasi target market brand X ada berapa persentase loyal user dari brand tersebut. Berikut ini adalah data yang saya dapatkan:
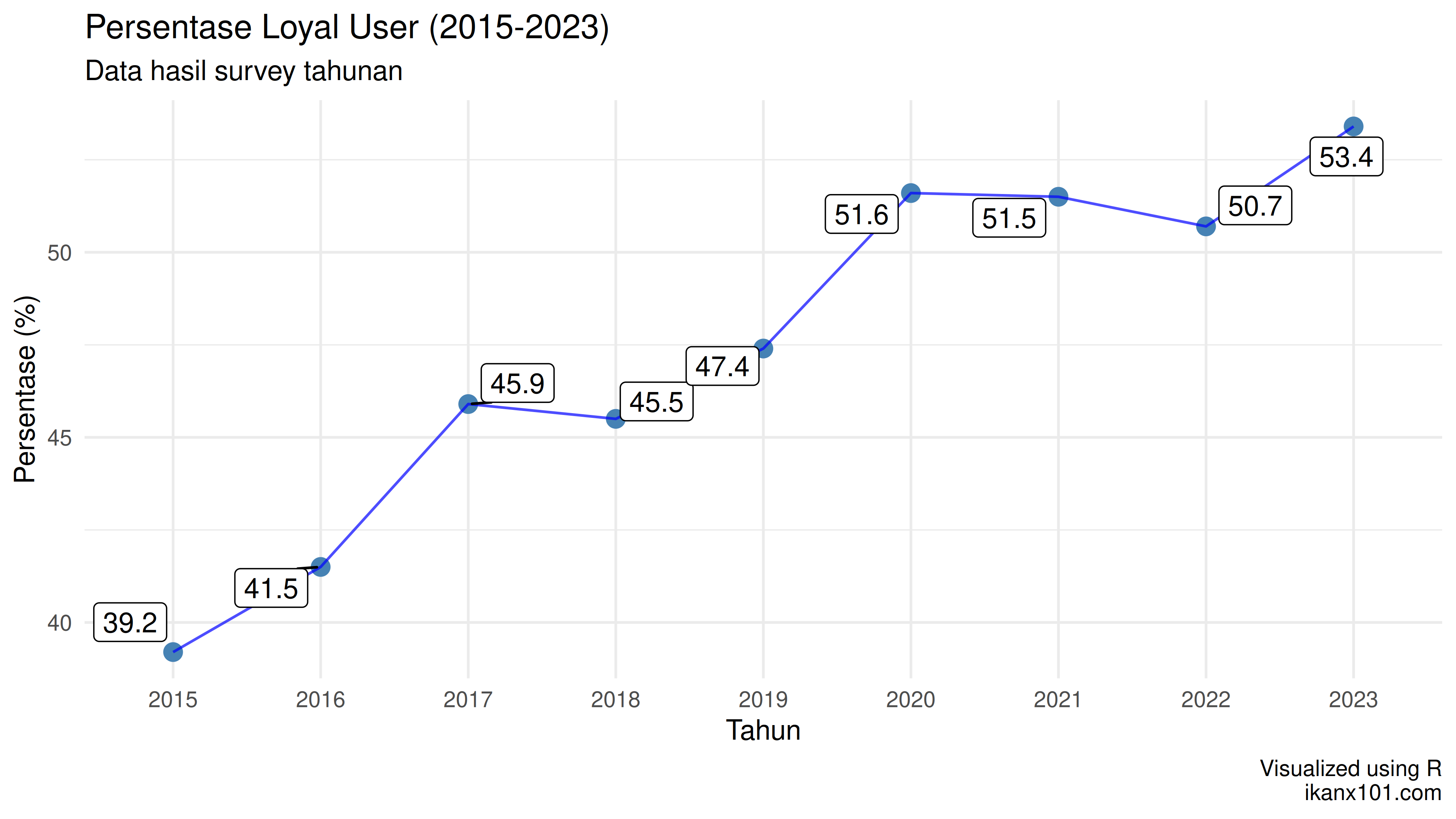
Business question yang kami hadapi cukup sederhana secara kalimat tapi sangat dalam secara konteks, yakni: tim marketing ingin mengetahui bagaimana tren perubahan persentase loyal user ke depannya.
“Apa tren jangka panjang dari loyal user? Seberapa yakin kita dengan estimasi tren ini?”
Kali ini saya akan menggunakan Bayesian untuk menjawab business question itu. Saya akan membuat regresi linear Bayesian yang menghubungkan tahun dengan persentase loyal user.
Apakah diperbolehkan membuat model regresi dari tahun yang memprediksi persentase loyal user?
Boleh saja TAPI dengan pemahaman dan interpretasi yang tepat. Saya menginterpretasikan model regresi ini sebagai:
Terdapat tren peningkatan sebesar X% per tahun dalam data loyal user kita. Tren ini kemungkinan disebabkan oleh faktor-faktor yang berkorelasi dengan waktu, seperti peningkatan kematangan produk, akumulasi pengalaman pengguna, atau perubahan lingkungan eksternal.
Jadi kita tidak bisa mengatakan tahun mengakibatkan perubahan persentase loyal user.
Oke, saya akan buat model regresi linear Bayesian-nya:
SAMPLING FOR MODEL 'continuous' NOW (CHAIN 1).
Chain 1:
Chain 1: Gradient evaluation took 3.9e-05 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.39 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1:
Chain 1:
Chain 1: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 1: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 1: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 1: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 1: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 1: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 1: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 1: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 1: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 1: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 1: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 1: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 1:
Chain 1: Elapsed Time: 0.03 seconds (Warm-up)
Chain 1: 0.03 seconds (Sampling)
Chain 1: 0.06 seconds (Total)
Chain 1:
SAMPLING FOR MODEL 'continuous' NOW (CHAIN 2).
Chain 2:
Chain 2: Gradient evaluation took 1.5e-05 seconds
Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.15 seconds.
Chain 2: Adjust your expectations accordingly!
Chain 2:
Chain 2:
Chain 2: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 2: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 2: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 2: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 2: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 2: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 2: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 2: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 2: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 2: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 2: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 2: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 2:
Chain 2: Elapsed Time: 0.028 seconds (Warm-up)
Chain 2: 0.029 seconds (Sampling)
Chain 2: 0.057 seconds (Total)
Chain 2:
SAMPLING FOR MODEL 'continuous' NOW (CHAIN 3).
Chain 3:
Chain 3: Gradient evaluation took 1.6e-05 seconds
Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0.16 seconds.
Chain 3: Adjust your expectations accordingly!
Chain 3:
Chain 3:
Chain 3: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 3: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 3: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 3: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 3: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 3: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 3: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 3: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 3: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 3: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 3: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 3: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 3:
Chain 3: Elapsed Time: 0.029 seconds (Warm-up)
Chain 3: 0.029 seconds (Sampling)
Chain 3: 0.058 seconds (Total)
Chain 3:
SAMPLING FOR MODEL 'continuous' NOW (CHAIN 4).
Chain 4:
Chain 4: Gradient evaluation took 2e-05 seconds
Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.2 seconds.
Chain 4: Adjust your expectations accordingly!
Chain 4:
Chain 4:
Chain 4: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 4: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 4: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 4: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 4: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 4: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 4: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 4: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 4: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 4: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 4: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 4: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 4:
Chain 4: Elapsed Time: 0.039 seconds (Warm-up)
Chain 4: 0.025 seconds (Sampling)
Chain 4: 0.064 seconds (Total)
Chain 4:
stan_glm
family: gaussian [identity]
formula: persentase ~ tahun_std
observations: 9
predictors: 2
------
Median MAD_SD
(Intercept) 47.4 0.5
tahun_std 1.7 0.2
Auxiliary parameter(s):
Median MAD_SD
sigma 1.6 0.4
------
* For help interpreting the printed output see ?print.stanreg
* For info on the priors used see ?prior_summary.stanreg
Perlu saya ingatkan bahwa formula regresi yang diharapkan adalah:
Perbedaan regresi linear Bayesian dengan frequentist adalah
dan
bukan merupakan satu
nilai pasti tapi berupa variabel acak dengan distribusi tertentu.
Berikut ini adalah trace plot dan density plot dari
dan
:
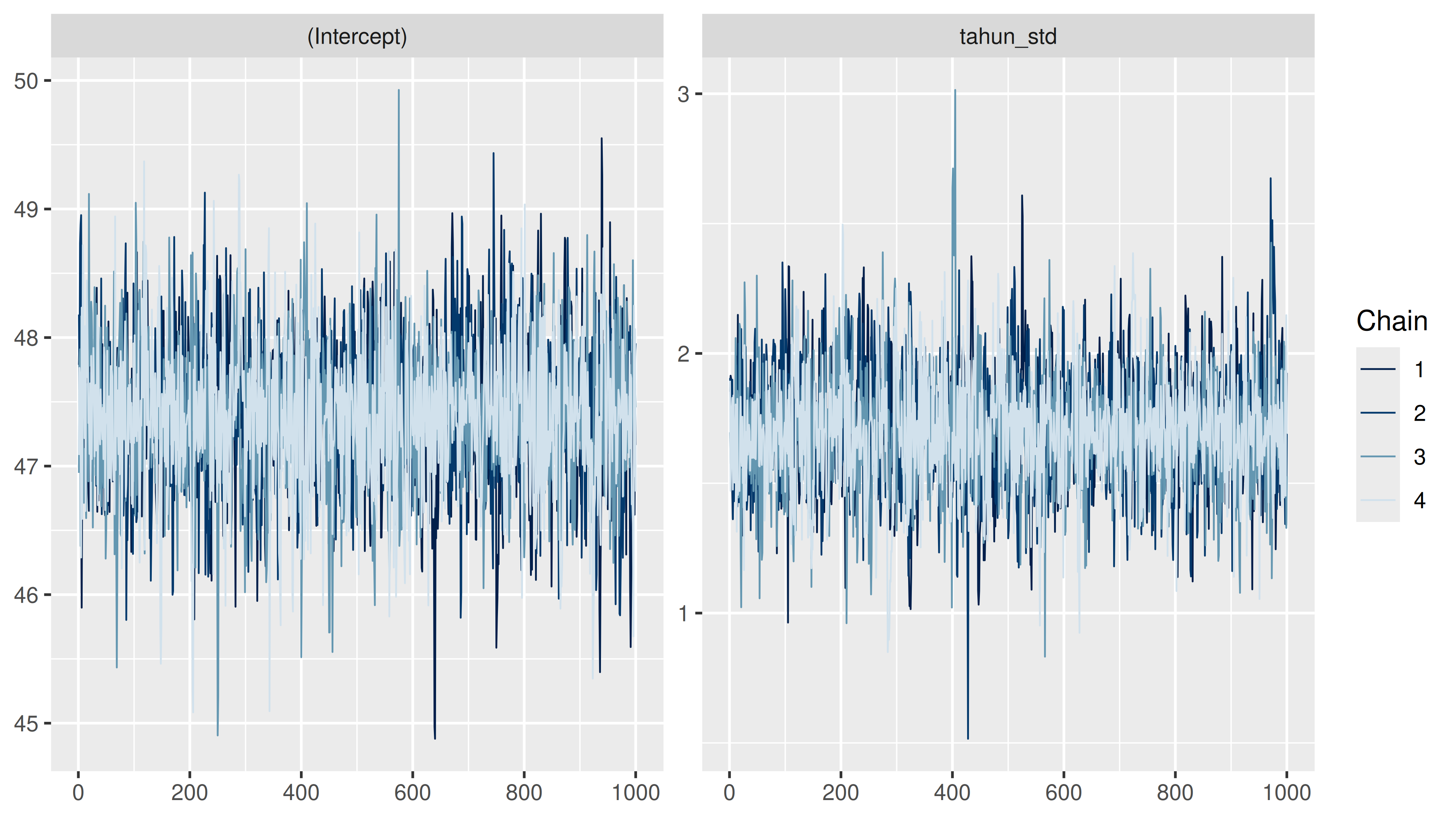
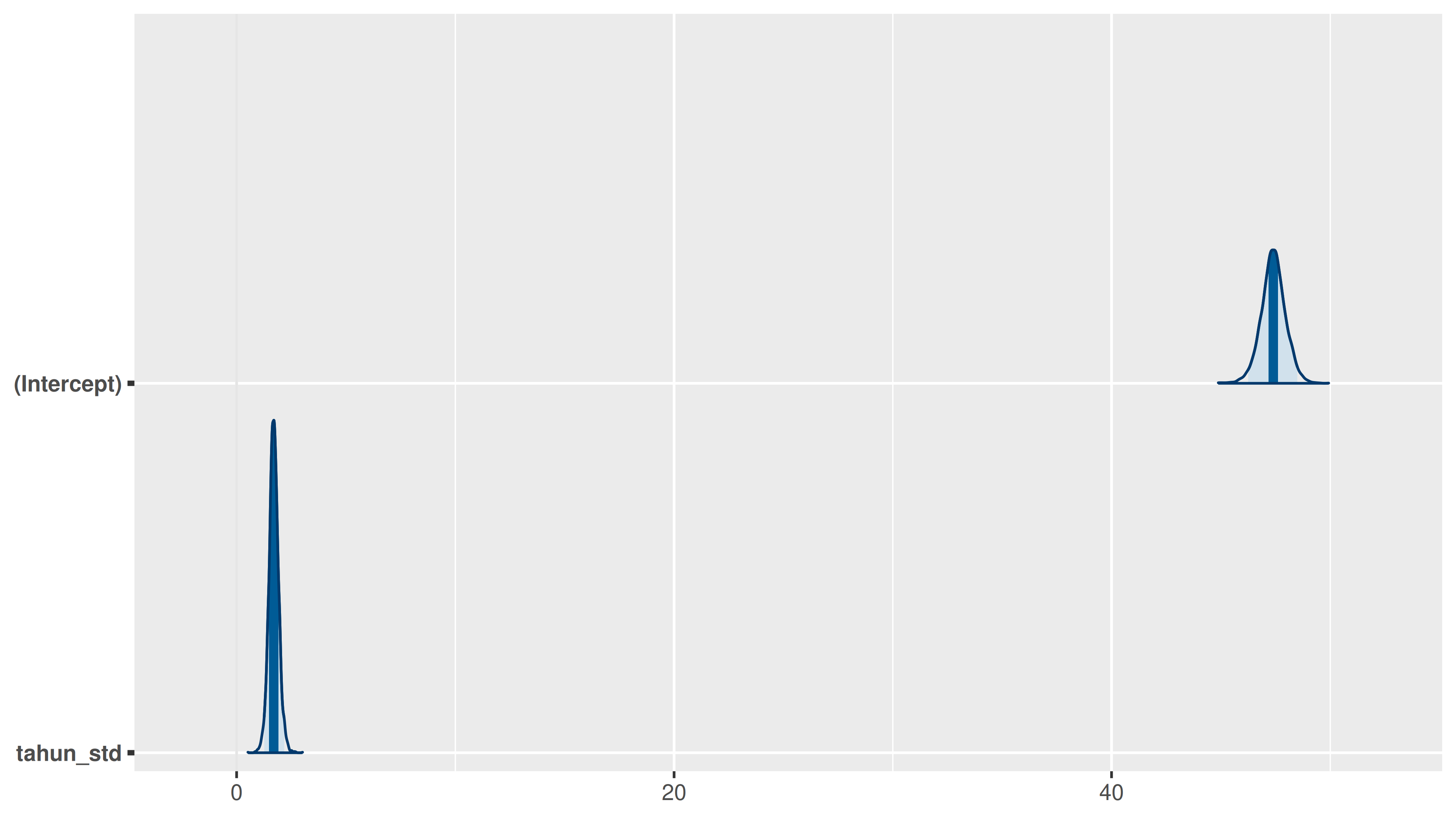
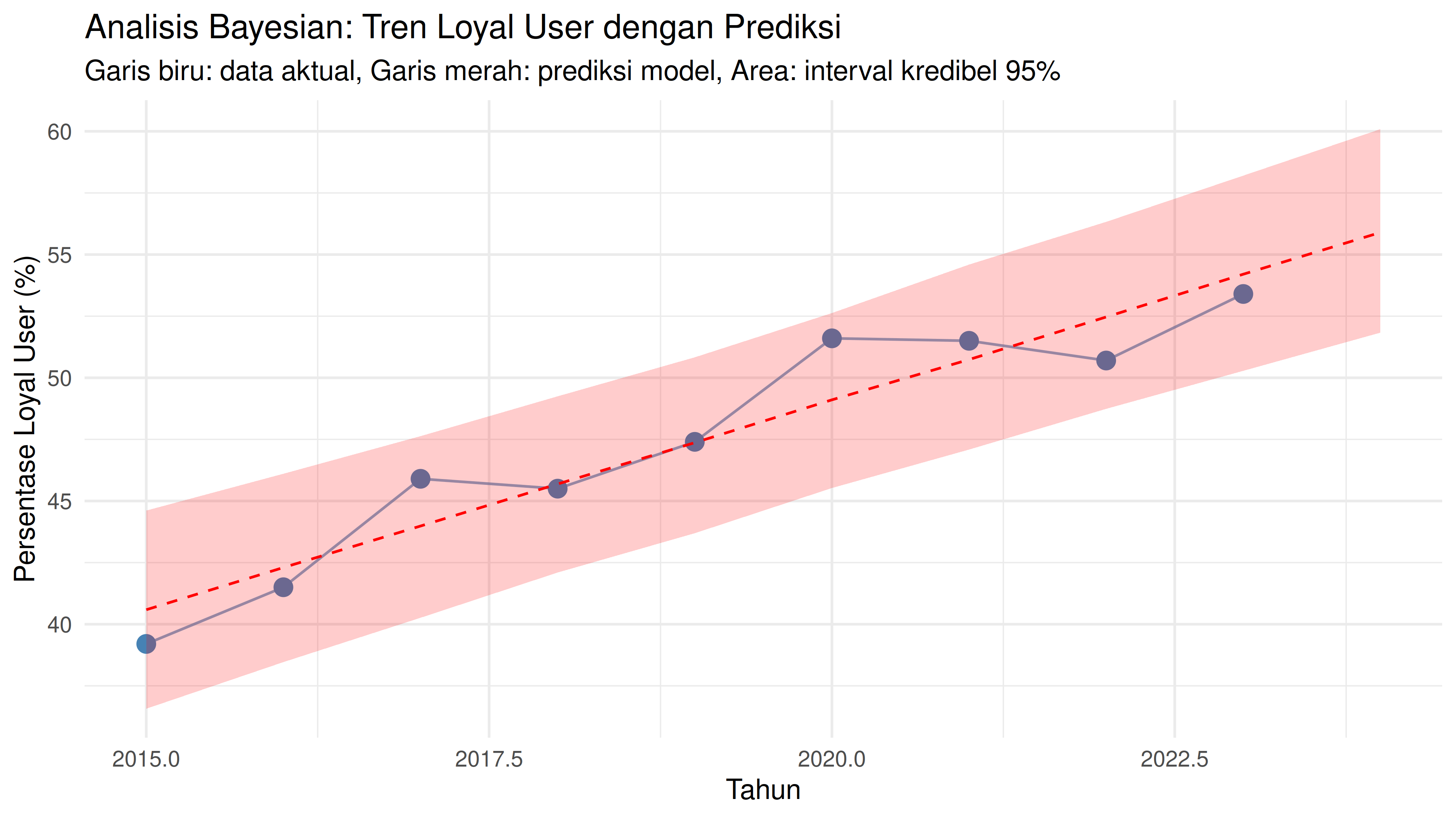
Sekarang kita akan lihat density plot dari nilai real persentase loyal user dengan nilai prediksi dari model:
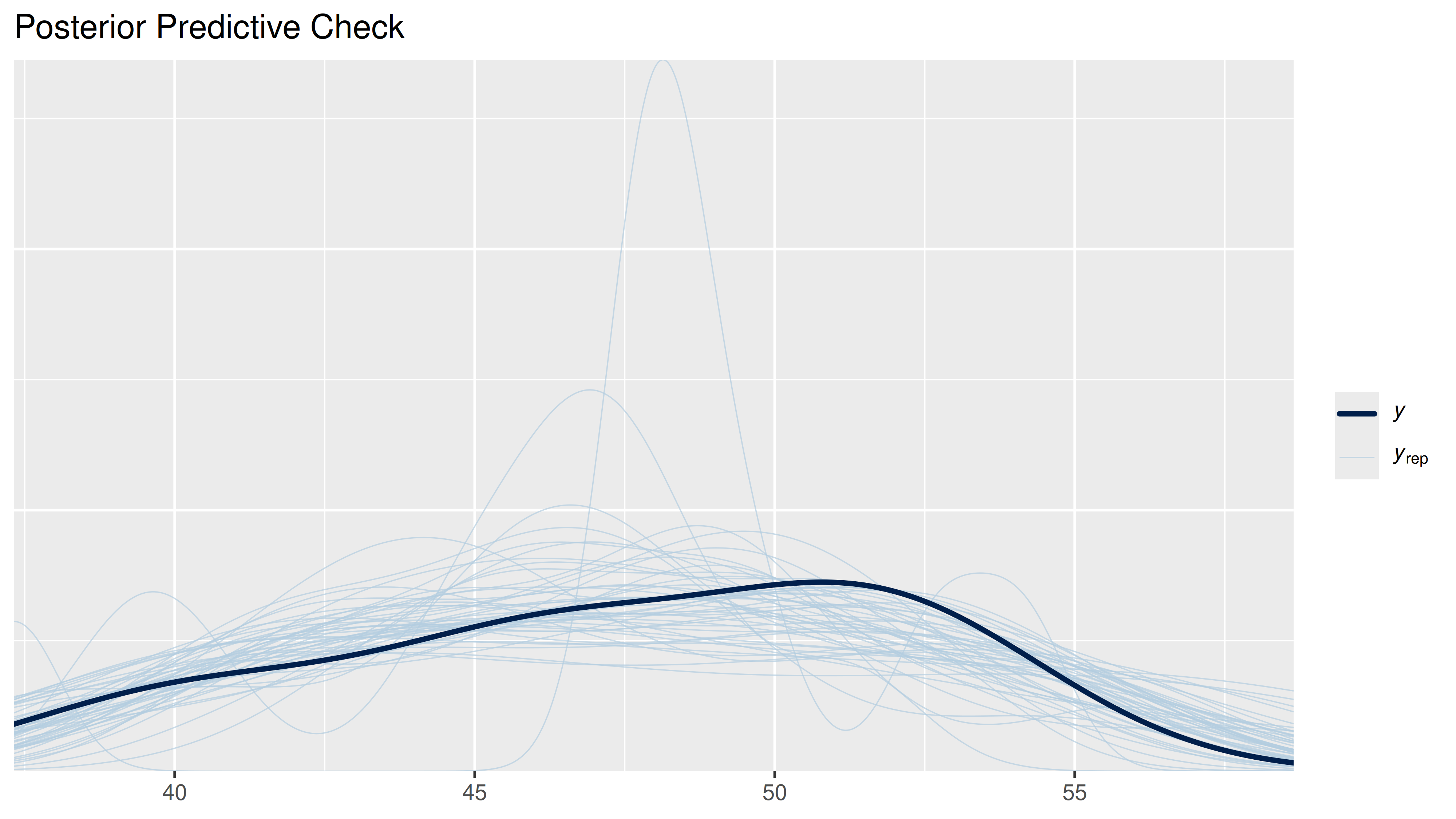
Jika kita lihat grafik di atas, semua kemungkinan nilai prediksi cukup
menggambarkan nilai real-nya. Sekarang saya akan analisa slope (atau
) dari
formula:
Probabilitas tren positif: 100 %
Interval kredibel 95% untuk tren tahunan:
2.5% 50% 97.5%
1.260621 1.697325 2.171231
Estimasi tren tahunan (dalam persentase poin per tahun):
Rata-rata: 1.701
SD: 0.225
Saya dapatkan bahwa
atau
slope selalu bernilai positif. Kita bisa simpulkan bahwa tren
persentase loyal user selalu naik setiap tahunnya. Sekarang saya akan
buat prediksi persentase loyal user pada tahun 2024:
Prediksi untuk tahun 2024:
2.5% 25% 50% 75% 97.5%
51.86247 54.61682 55.91519 57.17998 59.97931
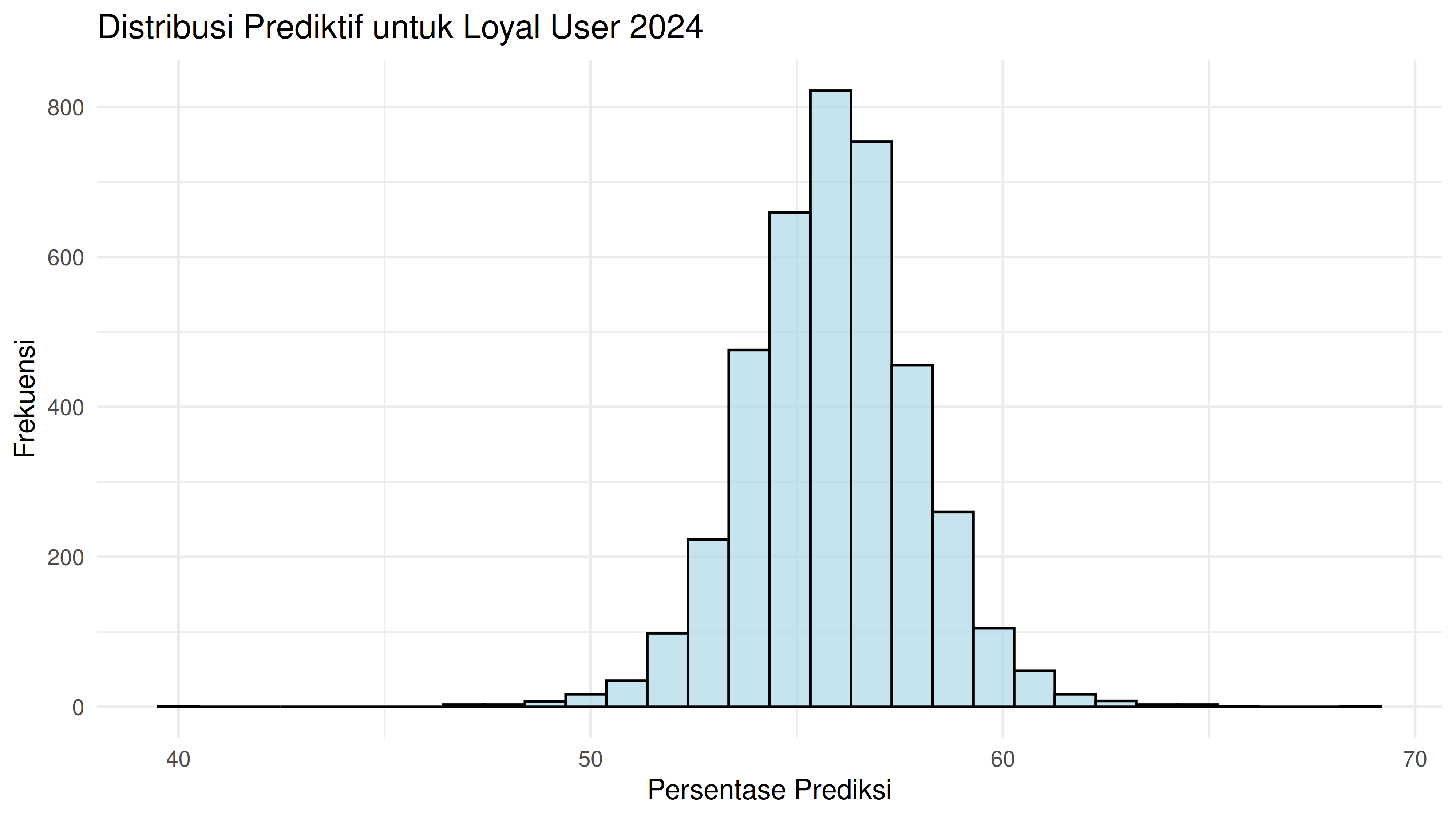
Seandainya kita memiliki target persentase loyal user pada 2024 sebesar 56%, apakah hal tersebut mungkin terjadi?
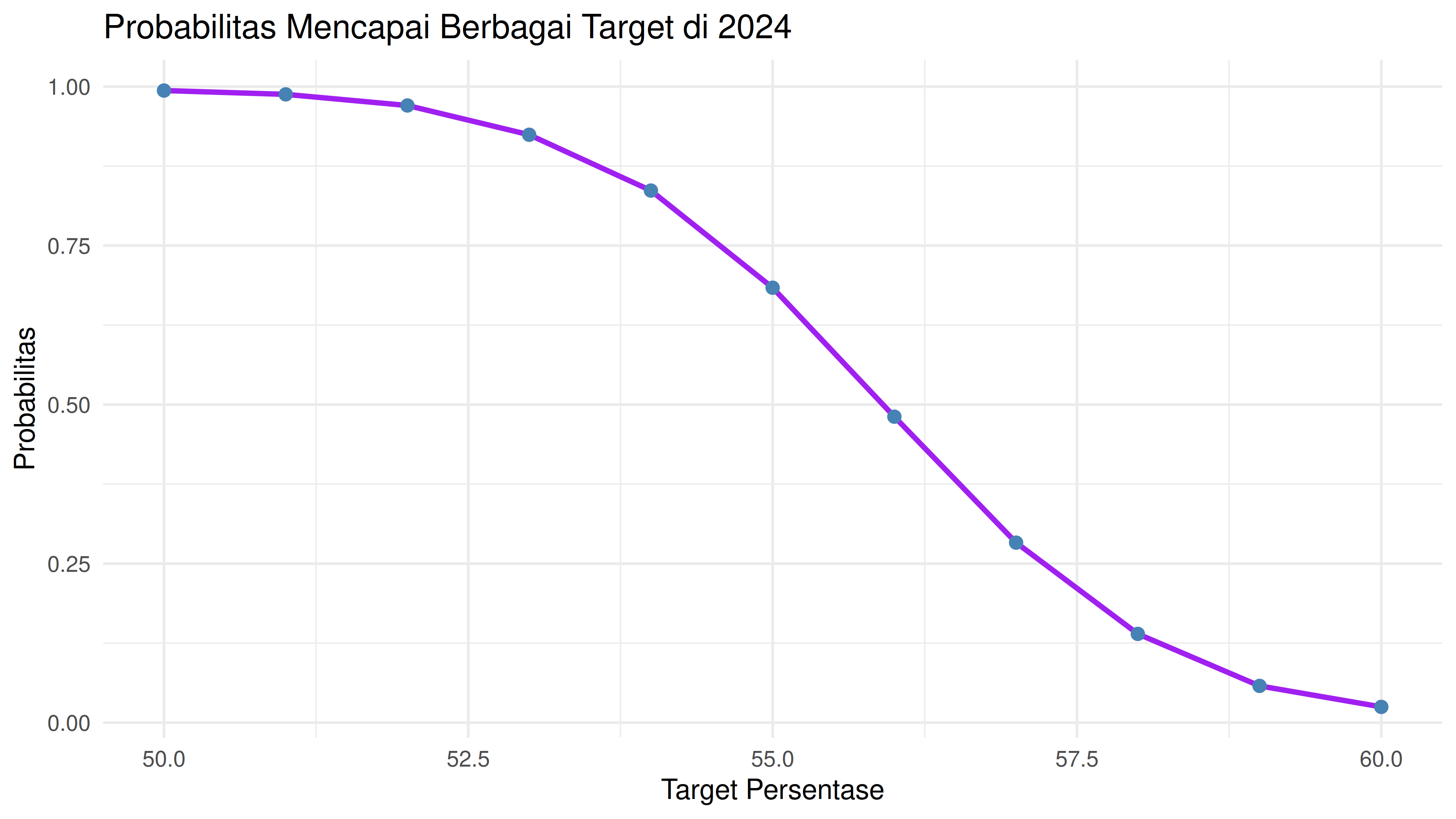
Probabilitas mencapai target 56% di 2024: 48.1 %
Kita bisa lihat bahwa peluang persentase loyal user mencapai 56% adalah sekitar 48%.
Summary
Dari paparan di atas, saya bisa menjawab business question yang diajukan. Tren persentase loyal user cenderung terus meningkat seiring dengan waktu. Namun hal ini bisa jadi berubah saat ada data baru yang masuk.
if you find this article helpful, support this blog by clicking the ads.
