Forecast Harga Emas Harian Menggunakan Bayesian Time Series

Pada enam bulan belakangan ini, saya merasa sering membaca dan mendengar berita tentang harga emas yang memiliki tren kenaikan. Kenaikan harga emas tentunya dipengaruhi oleh berbagai macam faktor. Menurut apa yang saya baca, kenaikan ini justru menjadi salah satu indikator dari kondisi ekonomi yang tidak baik, misalnya:

1. Ketidakpastian ekonomi global,
2. Ketakutan akan resesi atau krisis keuangan,
3. Inflasi tinggi.

Salah seorang rekan kerja saya yang selama ini menabung emas girang akan kondisi ini karena dia memiliki simpanan emas batangan yang dibelinya pada harga Rp600.000 per gram. Kemarin dia bercerita bahwa ia menjual emasnya pada saat harga per gramnya mencapai Rp2.200.000. Walaupun untung, ternyata ia tetap menyesal karena di beberapa hari setelahnya, harga emas hampir mencapai Rp2.500.000 per gram.

Oleh karena itu, dia bertanya kepada saya:

Bisa gak sih kita punya model forecast harga emas harian?

Untuk menjawab hal tersebut, kita bisa memilih berbagai macam pendekatan. Misalkan kita bisa mempertimbangkan menggunakan time series - based model seperti ARIMA, exponential smoothing, dan lain sebagainya. Kita juga bisa mempertimbangkan menggunakan deep learning-based model seperti:

1. Keras forecasting.
2. Meta Prophet.

Kali ini, saya akan mencoba metode lain untuk bisa forecasting harga emas selama 7 hari ke depan. Metode yang digunakan adalah Bayesian Time Series.

Berhubung ini hanya untuk keperluan blog, jadi saya tak akan serius-serius banget ya. hehe.

---

Data yang Digunakan

Saya mengambil data harga emas per gram harian dari situs Bullion Rates. Proses pengambilan data tersebut dibantu oleh Microsoft Copilot. Berikut adalah grafiknya:

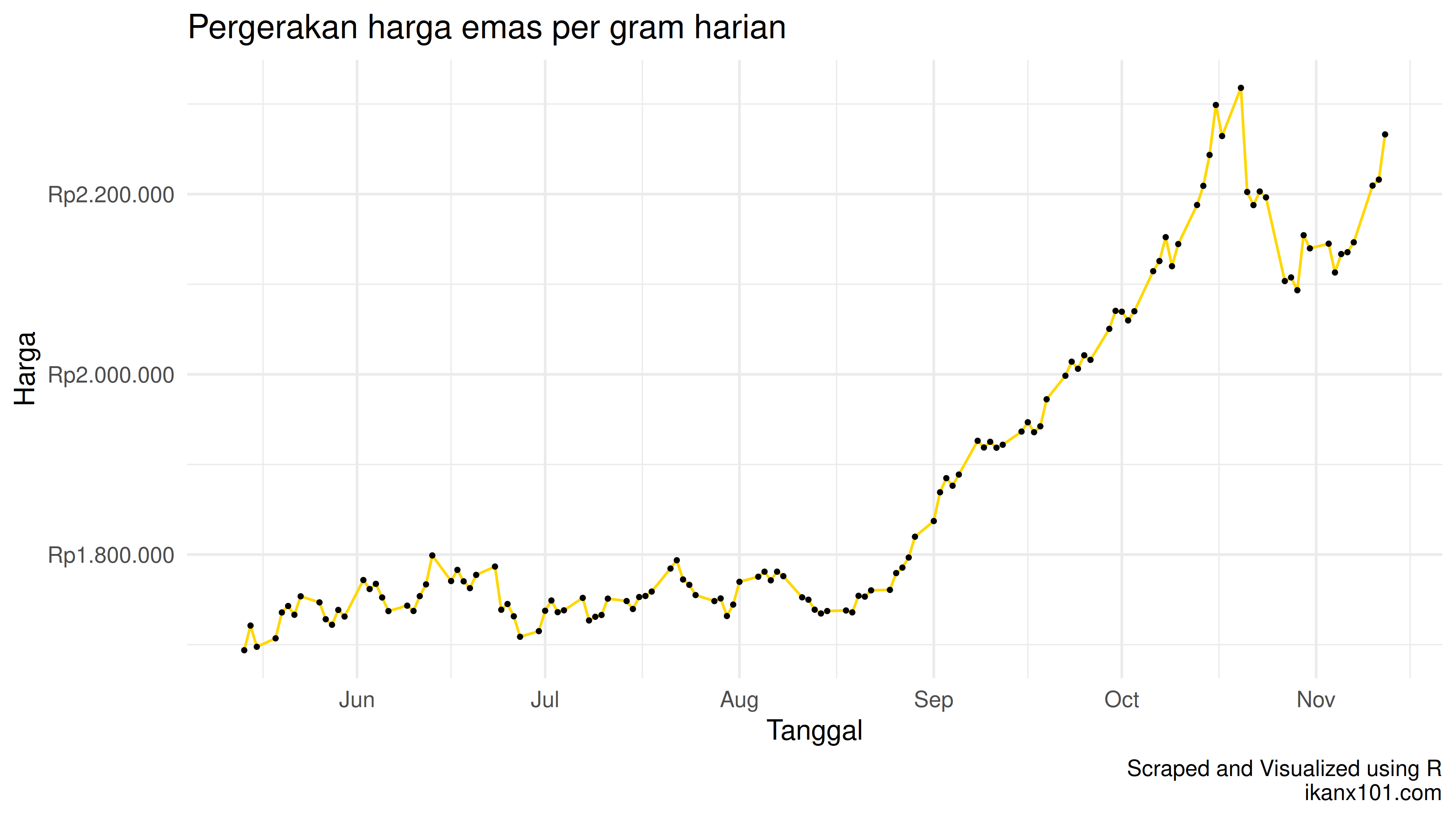
Melakukan forecasting dengan Bayesian Time Series tetap menggunakan prinsip prior dan posterior.

Prinsip Dasar: Belajar dari Pengalaman

Metode Bayesian pada intinya adalah tentang memperbarui keyakinan (belief) ketika ada data baru. Misalkan kita punya toko kue:

1. Keyakinan Awal (Prior): Sebelum toko buka, kita sudah punya “firasat” atau perkiraan berdasarkan pengalaman. Misalnya, “Biasanya kita bisa menjual 40-60 kue sehari (rata-rata 50).” Ini adalah “Prior” — perkiraan awal sebelum melihat data hari itu.
2. Data Nyata (Evidence): Hari ini, kita melihat cuaca mendung dan ada acara festival di dekat toko. Data baru ini akan mempengaruhi penjualan kita.
3. Keyakinan yang Diperbarui (Posterior): Kita menggabungkan “firasat awal” dengan “data baru” tersebut. Akhirnya kita bisa menyimpulkan, “Oke, dengan kondisi seperti ini, kemungkinan besar kita akan menjual 70-90 kue hari ini.” Keyakinan yang diperbarui inilah yang disebut “Posterior”.

Menerapkannya pada Data Runtun Waktu (Time Series)

Data time series pada kasus ini adalah data penjualan kue harian toko kita. Dalam Bayesian Time Series, kita melakukan proses update keyakinan setiap kali ada data baru masuk.

• Hari 1: Kita mulai dengan Prior (misalnya, prediksi 50 kue). Saat toko tutup, ternyata terjual 55 kue. Update keyakinan! Mungkin prediksi untuk besok menjadi 53 kue.
• Hari 2: Dengan Prior baru (53 kue), ternyata terjual 60 kue. Update lagi! Prediksi untuk lusa mungkin naik jadi 57 kue.
• Hari 3, 4, 5, dan seterusnya: Proses ini terus berulang. Setiap hari, model kita menjadi semakin “pintar” karena terus belajar dari data terbaru.

Untuk melakukan forecast, saya membuat algoritma di R menggunakan library(bsts). Berikut adalah hasil forecast yang saya lakukan:

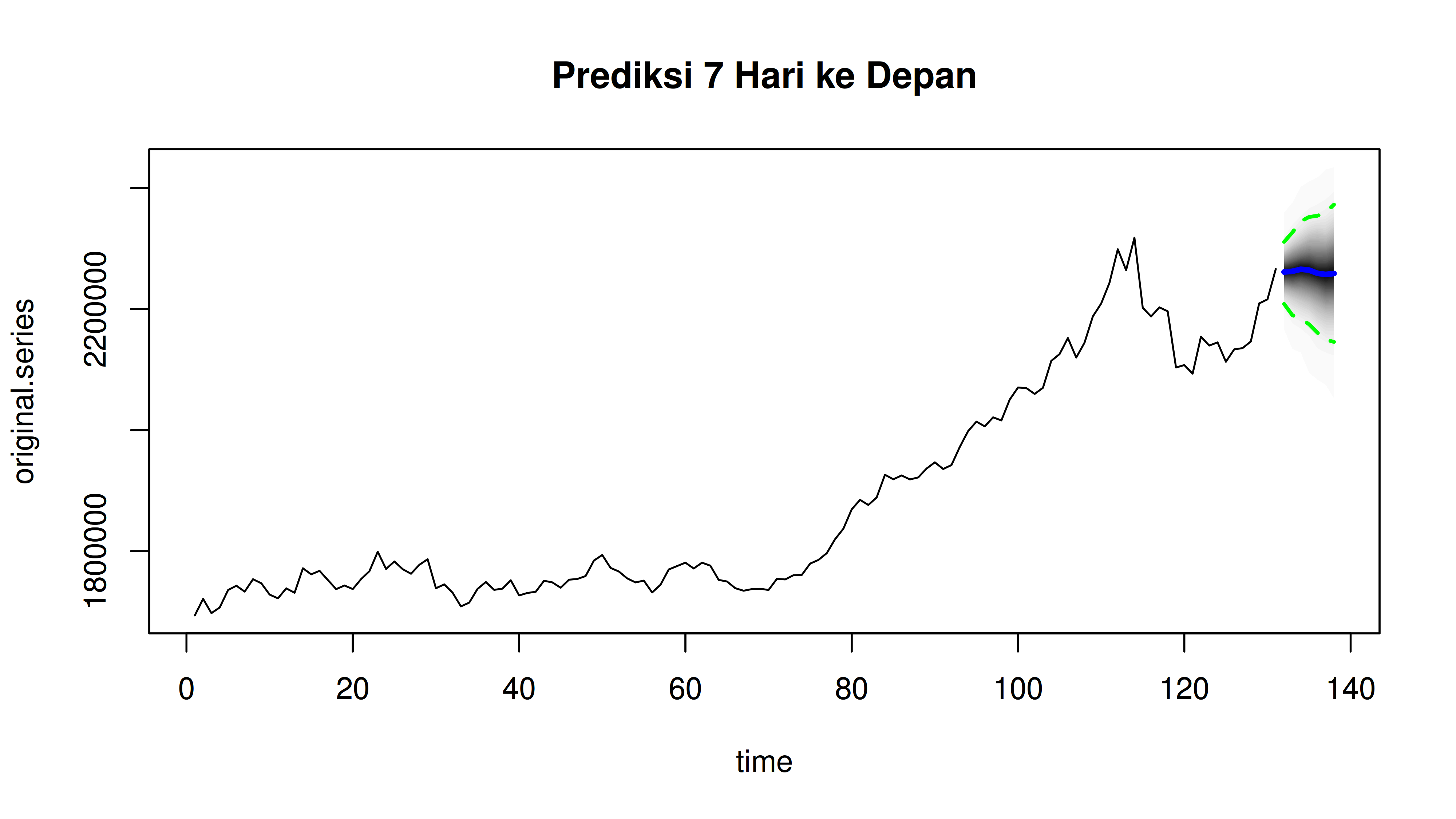
Kelebihan dari Bayesian adalah output yang dihasilkan merupakan range (bukan single point). Range tersebut memberikan kita interval di mana harga emas di hari ke depan kemungkinan besar (95%) berada di sana. Berikut adalah forecast 7 hari ke depan:

Day	Predicted_Date	Mean_Price	Median_Price	Lower_95	Upper_95
1	2025-11-13	Rp2,261,000	Rp2,261,345	Rp2,208,556	Rp2,311,112
2	2025-11-14	Rp2,262,414	Rp2,262,516	Rp2,189,813	Rp2,326,784
3	2025-11-15	Rp2,264,893	Rp2,265,819	Rp2,184,193	Rp2,345,009
4	2025-11-16	Rp2,264,651	Rp2,264,532	Rp2,174,935	Rp2,352,187
5	2025-11-17	Rp2,259,958	Rp2,259,154	Rp2,161,103	Rp2,354,278
6	2025-11-18	Rp2,256,255	Rp2,257,355	Rp2,149,386	Rp2,359,331
7	2025-11-19	Rp2,259,593	Rp2,258,833	Rp2,145,843	Rp2,372,779

Jika dilihat, masih ada tren harga stagnan dari expected price-nya (mean dan median). Kemudia jika kita lihat rentang forecast-nya (lower dan upper), semakin hari semakin lebar.

Saya menduga hal ini terjadi karena ketidakpastian saat forecasting jarak jauh menjadi lebih tinggi dibandingkan jarak dekat.

Diagnostik Model

Seberapa bagus model saya?

Saya akan melihat beberapa parameter goodness of fit dari model sebagai berikut:

$residual.sd
[1] 9392.941

$prediction.sd
[1] 25759.12

$rsquare
[1] 0.9972496

Bagaimana menginterpretasikan parameter tersebut?

Analoginya bayangkan kita seorang penembak jitu dan sedang latihan menembak target di lapangan tembak.

• Targetnya adalah nilai sebenarnya (actual value) dari data.
• Peluru kita adalah nilai prediksi (forecasted value) dari model tersebut.
• Lubang peluru di papan target adalah titik di mana peluru kita kena.

Apa Itu Residual Standard Deviation (Residual SD)?

Residual adalah jarak antara lubang peluru dengan titik pusat target. Residual SD adalah ukuran sebaran atau konsistensi dari semua jarak kesalahan (residual) tebakan model kita.

Misalkan ada dua penembak:

1. Penembak A: Tembakannya tersebar acak, ada yang 1 cm dari pusat, ada yang 5 cm, ada yang 3 cm. Artinya residual SD-nya besar.
2. Penembak B: Hampir semua tembakannya mengelompok rapat di sekitar bullseye, misalnya hanya berjarak 0.5 cm sampai 1.5 cm. Artinya residual SD-nya kecil.

Jadi, Residual SD mengukur tingkat akurasi dan konsistensi model kita.

Model kita memiliki Residual SD sebesar Rp9.392.

Apa Itu Prediction Standard Deviation?

Prediction SD adalah ukuran ketidakpastian untuk prediksi masa depan.

Bayangkan kita sedang memprediksi harga emas besok:

• Model kita memberi prediksi: Rp1.200.000.
• Prediction SD: Rp10.000.

Artinya adalah prediksi terbaik yang bisa kita berikan adalah

Prediksi terbaik Anda adalah Rp 1.200.000 dengan ketidakpastian ± Rp10.000.

Model kita memiliki Prediction SD sebesar Rp25.759.

Apa itu R-square (R²) dalam Bayesian Time Series?

R-square adalah “persentase penjelasan”. Analoginya adalah dari total variasi dalam harga emas harian, berapa persen yang bisa dijelaskan oleh model tersebut?

Model kita memiliki R-square sebesar 0.9972496.

---

Kesimpulan dan Penutup

Jika kita perhatikan kembali data harga emas pada rentang waktu yang sangat lama, harga emas cenderung selalu meningkat seiring waktu. Hal ini juga tergambar dari hasil forecast model secara singkat (7 hari). Namun bisa jadi ada fluktuatif dengan tren secara panjang tetap naik harganya.