Berkenalan dengan Black Hole Optimization Algorithm

26 minute read

Pada posting sebelumnya saya membahas salah satu meta heuristic algorithm bernama Spiral Dynamic Optimization Algorithm (SDOA).

Kali ini saya akan kembali membahas salah satu meta heuristic algorithm yang menurut saya sangat simpel kerjanya. Algoritmanya mirip sekali dengan SDOA namun tanpa harus melakukan rotasi. Hal ini sangat berguna saat menghadapi variabel yang banyak sehingga tidak memberatkan komputer saat melakukan komputasi matriks rotasi berukuran besar.

Algoritma ini terinspirasi dari salah satu fenomena alam, yakni black hole. Ada beberapa paper yang membahas tentang algoritma ini. Kelak saya akan meramu beberapa temuan dan improvement yang saya dapatkan dari papers tersebut dan membuat modifikasi algoritmanya menjadi: Big Bang - Black Hole Inspired Optimization Algorithm.

Berbeda dengan solusi eksak yang sudah pasti menghasilkan solusi paling optimal, solusi hasil perhitungan meta heuristic belum tentu menghasilkan solusi paling optimal.

Kenapa demikian? Karena setiap algoritmanya mengandung unsur keacakan.

Konon setiap kejadian yang terjadi di dunia terjadi secara acak.

Namun dengan melakukan beberapa improvements, kita bisa mendapatkan solusi yang optimal dari perhitungan meta heuristic.

OPTIMISASI

Masalah optimisasi yang ada di matematika sebenarnya adalah masalah pencarian nilai maksimum atau minimum. Terlepas dari apakah ada constraints atau tidak.

Oleh karena itu, ada dua istilah yang sering muncul saat kita berbicara mengenai hal ini:

Local optima: nilai maksimum atau minimum yang terjadi di selang tertentu. Bukan merupakan solusi dari keseluruhan daerah definisi.
Global optimum: nilai maksimum atau minimum yang terjadi di daerah definisi. Tentunya ini adalah solusi yang dicari.

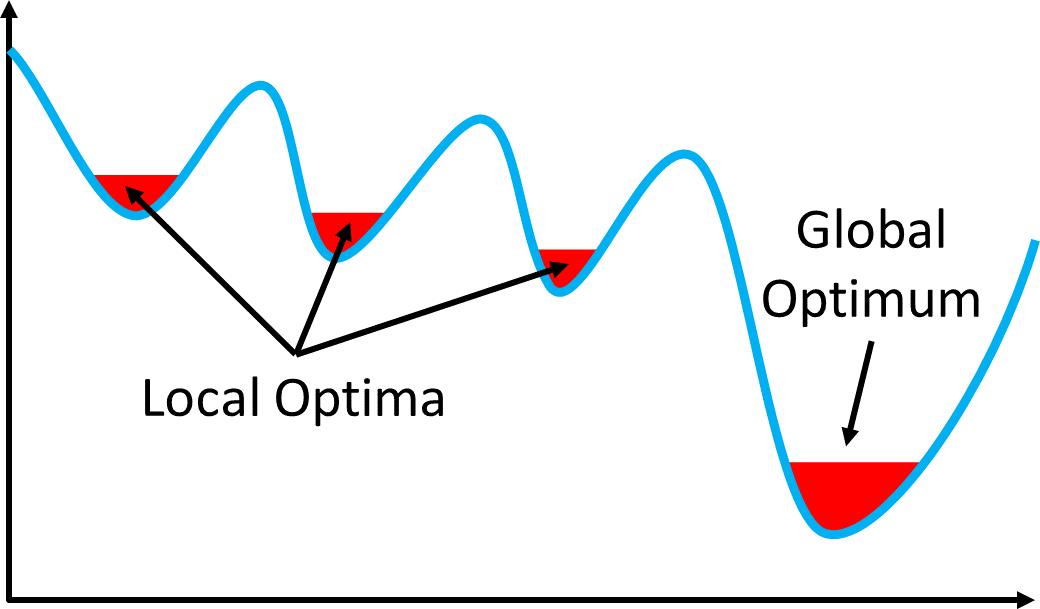
Aplikasi Algoritma Optimisasi

Untuk apa sih kita menggunakan algoritma meta heuristic ini?

Menyelesaikan permasalahan yang ditemui…

Lebih besar dari masalah yang kkita hadapi saat training optimisasi di KampusX silam. Aplikasi algoritma ini sangat banyak, mulai dari:

Penyelesaian masalah optimisasi (baik linear atau non linear).
- Bisa untuk menyelesaikan objective function yang linear atau tidak linear.
- Bisa untuk menyelesaikan berbagai macam tipe variabel: diskrit, kontinu, dan biner.
- Bisa untuk menyelesaikan constrained problem dan unconstrained problem.
Feature selection untuk:
- Machine learning model.
- Deep learning model.
- Baik untuk permasalahan klasifikasi dan regresi.
dll (tergantung imajinasi Anda).

Kita akan bahas satu-persatu di bagian selanjutnya.

BIG BANG - BLACK HOLE INSPIRED OPTIMIZATION ALGORITHM

BHO merupakan salah satu algoritma optimisasi meta heuristic yang terinspirasi dari kejadian big bang hingga kemunculan black hole sehingga memakan objek angkasa yang lain.

Prinsip kerjanya sederhana, yakni:

Membuat suatu big bang, mengakibatkan banyak bintang lahir.
Menjadikan salah satu bintang sebagai black hole.
Menarik semua bintang lain menuju black hole karena gravitasinya.
Saat bintang masuk ke area event horizon dari black hole, maka bintang tersebut akan hilang.
Saat jumlah bintang berkurang karena tertarik ke black hole, bintang-bintang baru akan bermunculan.

Bintang yang kita sebutkan di atas sejatinya adalah calon solusi sementara black hole adalah solusi yang dicari.

Ilustrasi

Untuk memudahkan, lihatlah ilustrasi dari bintang-bintang sebagai berikut:

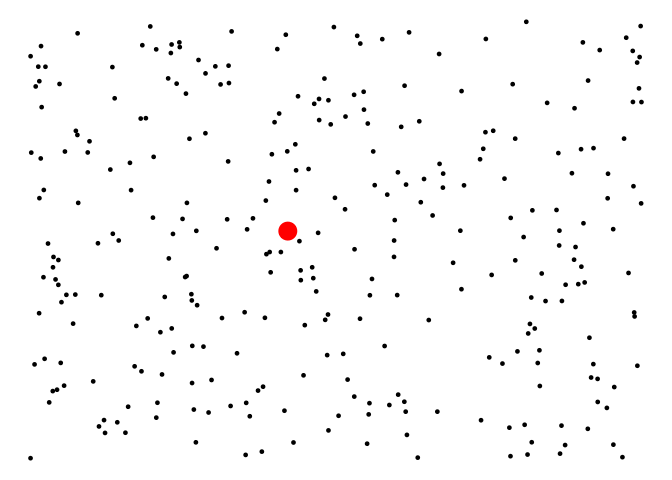
Misalkan titik merah adalah titik solusi yang dicari. Maka titik merah akan menjadi black hole yang menyerap semua bintang yang ada dengan suatu nilai gravity rate tertentu.

Beberapa kritik atas algoritma ini adalah kelemahannya untuk mencari global optima. BHO cenderung mudah terjebak dalam local optima (seolah-olah local optima adalah solusi yang dicari sehingga menjadikan black hole terlalu cepat memakan bintang yang lain). Sementara kemampuannya dalam mengeksplorasi area lainnya menjadi lemah. Oleh karena itu kita bisa melakukan beberapa improvement dengan mengubah cara perhitungan gravity rate dan menambahkan another big bang jika banyaknya bintang semakin sedikit.

Hal Penting dalam BHO

Setidaknya ada dua hal yang perlu didefinisikan dalam BHO, yakni:

Gravity rate
Radius event horizon

Gravity rate

Agar BHO bisa mengeksploitasi area definisi lebih baik, maka gravity rate didefinisikan sebagai:

$g = \text{random}(0,1.5)$

Nilai random antara [0,1.5].

Hal ini memastikan adanya konstraksi dan relaksasi bintang ke area-area lainnya.

Radius event horizon

Radius event horizon bisa kita definisikan:

$r = \frac{f_{bh}}{\sum{f_{xi}}}$

Pseudocode

Misalkan kita hendak mencari $x \in D$ yang menyebabkan $\min{f(x)}$ . Pseudocode dari algoritma ini adalah:

STEP I
  define:
    max_iter
  generate stars randomly
    xi
STEP II
  evaluate all xi
    fxi
STEP III
  define black hole (xi that produce min(fxi)) 
    x*
  define gravity rate (constant or not)
    g in [0,1]
  define event horizon radius
    r = f(x*) / sum(f(xi))
STEP IV
  pull all stars into black hole at gravity rate
    xi' = x* + g (x* - xi)
  eliminate all stars in event horizon radius
    if d(x*,xi) < r :
      delete xi
STEP V
  if number of stars getting lower:
    generate stars all over
STEP VI
  loop STEP II to STEP V all over
  until 
    converge or
    max iteration

MAXIMIZING / MINIMIZING

Contoh

Cari $x,y$ yang membuat $f(x,y) = x^2 + y^2$ minimum di $x,y \in [-1,1]$

# dimulai dari hati yang bersih
rm(list=ls())
library(dplyr)

# definisi fungsi soal
f = function(vec) vec[1]^2 + vec[2]^2

# definisi fungsi generate star
big_bang = function() runif(2,-1,1) %>% round(1)

# definisi 
# berapa banyak bintang
N = 500
stars = vector("list",N)
# rumah untuk fxi
fxi = rep(999,N)
# definisikan dulu max iteration yang diperbolehkan
max_iter = 600

# membuat bintang dan menghitung nilai fxi-nya
for(i in 1:N){
  stars[[i]] = big_bang()
  fxi[i] = f(stars[[i]])
}

# mencari black hole
n_bh = which.min(fxi) # star ke berapa yang punya nilai fxi terkecil
bh = stars[[n_bh]] # definisi black hole
f_bh = fxi[n_bh] # nilai f_bh

# iterasi BHO kita mulai dari sini
for(ikang in 1:max_iter){
  # menghitung radius event horizon
  r = f_bh / sum(fxi)

  # saat ada bintang yang berjarak kurang dari r akan kita hapus
  jarak = abs(fxi - f_bh)
  n_luar = which(jarak >= r)

  # stars yang ada di n_luar 
  stars = stars[n_luar]

  # jika jumlah stars < N --> big bang lagi
  n_stars = length(stars)
  if(n_stars < N){
    # membuat bintang dan menghitung nilai fxi-nya
    for(i in (n_stars + 1):N){
        stars[[i]] = big_bang()
        fxi[i] = f(stars[[i]])
    }
  }

  # gravity rate - akan dbuat tetap
  g = runif(1,0,1.5)

  # iterasi proses penarikan bintang ke black hole
  for(j in 1:N){
    xt = stars[[j]]
    xt_new = bh + g * (xt - bh)
    xt_new = xt_new %>% round(1)
    fxi[j] = f(xt_new)
    stars[[j]] = xt_new
  }

  # mencari black hole
  n_bh = which.min(fxi) # star ke berapa yang punya nilai fxi terkecil
  bh = stars[[n_bh]] # definisi black hole
  f_bh = fxi[n_bh] # nilai f_bh
}

n_solusi = which.min(fxi)
stars[[n_solusi]] %>% round(2)

## [1] 0 0

min(fxi)

## [1] 0

Contoh

Cari $x_1,x_2$ yang meminimumkan fungsi berikut ini:

$f(x_1,x_2) = \frac{x_1^4 - 16 x_1^2 + 5 x_1}{2} + \frac{x_2^4 - 16 x_2^2 + 5 x_2}{2} \\ -4 \leq x_1,x_2 \leq 4$

# dimulai dari hati yang bersih
rm(list=ls())

library(dplyr)

# definisi fungsi soal
f = function(vec) {
  ka = vec[1]^4 - 16 * vec[1]^2 + 5 * vec[1]
  ka = ka / 2
  ki = vec[2]^4 - 16 * vec[2]^2 + 5 * vec[2]
  ki = ki / 2
  return(ka + ki)
}

# definisi fungsi generate star
big_bang = function() runif(2,-4,4)

# definisi 
# berapa banyak bintang
N = 700
stars = vector("list",N)
# rumah untuk fxi
fxi = rep(999,N)
# definisikan dulu max iteration yang diperbolehkan
max_iter = 50

# membuat bintang dan menghitung nilai fxi-nya
for(i in 1:N){
  stars[[i]] = big_bang()
  fxi[i] = f(stars[[i]])
}

# mencari black hole
n_bh = which.min(fxi) # star ke berapa yang punya nilai fxi terkecil
bh = stars[[n_bh]] # definisi black hole
f_bh = fxi[n_bh] # nilai f_bh

# iterasi BHO kita mulai dari sini
for(ikang in 1:max_iter){
  # menghitung radius event horizon
  r = f_bh / sum(fxi)

  # saat ada bintang yang berjarak kurang dari r akan kita hapus
  jarak = abs(fxi - f_bh)
  n_luar = which(jarak >= r)

  # stars yang ada di n_luar 
  stars = stars[n_luar]

  # jika jumlah stars < N --> big bang lagi
  n_stars = length(stars)
  if(n_stars < N){
    # membuat bintang dan menghitung nilai fxi-nya
    for(i in (n_stars + 1):N){
        stars[[i]] = big_bang()
        fxi[i] = f(stars[[i]])
    }
  }

  # gravity rate - akan dbuat tetap
  g = runif(1,0,1.5)

  # iterasi proses penarikan bintang ke black hole
  for(j in 1:N){
    xt = stars[[j]]
    xt_new = bh + g * (xt - bh)
    fxi[j] = f(xt_new)
    stars[[j]] = xt_new
  }

  # mencari black hole
  n_bh = which.min(fxi) # star ke berapa yang punya nilai fxi terkecil
  bh = stars[[n_bh]] # definisi black hole
  f_bh = fxi[n_bh] # nilai f_bh
}

n_solusi = n_bh
stars[[n_solusi]] %>% round(2)

## [1] -2.89 -2.89

f_bh

## [1] -78.32576

PENCARIAN AKAR

Apa hubungannya optimisasi dengan pencarian akar?

Kita bisa mengubah masalah optimisasi menjadi masalah pencarian akar dengan cara:

Suatu sistem memiliki solusi $x = (x_1,x_2,..,x_n)^T$ jika $F(x)$ yang kita definisikan sebagai:

![F(x) = \frac{1}{1 + \sum_{i = 1}^n |g_i(x)|}](https://latex.codecogs.com/png.latex?F%28x%29%20%3D%20%5Cfrac%7B1%7D%7B1%20%2B%20%5Csum_%7Bi%20%3D%201%7D%5En%20%7Cg_i%28x%29%7C%7D “F(x) = \frac{1}{1 + \sum_{i = 1}^n

g_i(x)

}”)

memiliki nilai maksimum sama dengan 1.

Akibatnya algoritma yang sebelumnya adalah mencari nilai $\min{F(x)}$ diubah mencari $\max{F(x)}$ .

Akibatnya $x$ menjadi akar dari $g_i(x),\space i = 1,2,..,n$ .

Contoh Soal

Kita akan gunakan BHO untuk menyelesaikan permasalahan pencarian akar untuk persamaan diophantine berikut:

$x^2 + y^2 = 625, 0 \leq x,y \leq 25$

# dimulai dari hati yang bersih
rm(list=ls())

library(dplyr)

# definisi fungsi soal
f = function(vec) {
  g = vec[1]^2 + vec[2]^2 - 625
  g = abs(g)
  f = 1 / (1 + g)
  return(f)
}

# definisi fungsi generate star
big_bang = function() runif(2,-0.45,25.45) %>% round(0)

# definisi 
# berapa banyak bintang
N = 800
stars = vector("list",N)
# rumah untuk fxi
fxi = rep(999,N)
# definisikan dulu max iteration yang diperbolehkan
max_iter = 80

# membuat bintang dan menghitung nilai fxi-nya
for(i in 1:N){
  stars[[i]] = big_bang()
  fxi[i] = f(stars[[i]])
}

# mencari black hole
n_bh = which.max(fxi) # star ke berapa yang punya nilai fxi terkecil
bh = stars[[n_bh]] # definisi black hole
f_bh = fxi[n_bh] # nilai f_bh

# iterasi BHO kita mulai dari sini
for(ikang in 1:max_iter){
  # menghitung radius event horizon
  r = f_bh / sum(fxi)

  # saat ada bintang yang berjarak kurang dari r akan kita hapus
  jarak = abs(fxi - f_bh)
  n_luar = which(jarak >= r)

  # stars yang ada di n_luar 
  stars = stars[n_luar]

  # jika jumlah stars < N --> big bang lagi
  n_stars = length(stars)
  if(n_stars < N){
    # membuat bintang dan menghitung nilai fxi-nya
    for(i in (n_stars + 1):N){
        stars[[i]] = big_bang()
        fxi[i] = f(stars[[i]])
    }
  }

  # gravity rate - akan dbuat tetap
  g = runif(1,0,1.5)

  # iterasi proses penarikan bintang ke black hole
  for(j in 1:N){
    xt = stars[[j]]
    xt_new = bh + g * (xt - bh)
    xt_new_1 = xt_new %>% round(0)
    fxi[j] = f(xt_new_1)
    stars[[j]] = xt_new
  }

  # mencari black hole
  n_bh = which.max(fxi) # star ke berapa yang punya nilai fxi terkecil
  bh = stars[[n_bh]] # definisi black hole
  f_bh = fxi[n_bh] # nilai f_bh
}

stars[[n_bh]] %>% round(0)

## [1] 15 20

fxi[n_bh]

## [1] 1

OPTIMISASI

Bagaimana menyelesaikan mixed integer programming (baik linear dan non linear) menggunakan BHO?

Mengubah Constrained Optimization

Salah satu trik yang bisa dilakukan agar SOA bisa menyelesaikan mixed integer programming adalah dengan mengubah constrained optimization problem menjadi unconstrained optimization problem kemudian memanfaatkan penalty constant.

Misal suatu permasalahan MILP atau MINLP bisa ditulis secara umum sebagai berikut:

$\min_{x \in \mathbb{R}^n} f(x)$

$\text{subject to: } g_i(x) = 0, i = 1,2,..,M$

$\text{and } h_j(x) \leq 0,i = 1,2,..,N$

$x = (x_1,x_2,...,x_n)^T \in \mathbb{N}$

Bentuk di atas bisa kita ubah menjadi:

$F(x,\alpha,\beta) = f(x) + \sum_{i=1}^M \alpha_i g_i^2(x) + \sum_{j = 1}^N \beta_j (\max{(h_i(x),0)})^2$

dimana $\alpha,\beta$ merupakan penalty constant yang bisa dibuat sangat besar.

Contoh Soal

Oke, untuk contoh kasus pertama saya akan gunakan persoalan yang pernah saya tulis di blog sebelumnya.

Cari $(x,y)$ yang memaksimalkan $7000 x + 12000 y$ dengan constraints sebagai berikut:

$4x + 20y \leq 1960 \\ x + y \leq 250 \\ x,y \geq 0 \\ x,y \in \mathbb{Z}^+$

# dimulai dari hati yang suci
rm(list=ls())

# definisi fungsi soal
f1 = function(x){-7000*x[1] - 12000*x[2]}
h1 = function(x){4*x[1] + 20*x[2] - 1960}
h2 = function(x){x[1] + x[2] - 250}
# definisi penalty constant
beta = 10^25
# objective function final
f = function(x){
  el_1 = f1(x) 
  el_2 = beta * (max(h1(x),0))^2
  el_3 = beta * (max(h2(x),0))^2
  return(el_1 + el_2 + el_3)
}

# definisi fungsi generate star
big_bang = function() runif(2,-0.45,250) %>% round(0)

# definisi 
# berapa banyak bintang
N = 200
stars = vector("list",N)
# rumah untuk fxi
fxi = rep(999,N)
# definisikan dulu max iteration yang diperbolehkan
max_iter = 80

# membuat bintang dan menghitung nilai fxi-nya
for(i in 1:N){
  stars[[i]] = big_bang()
  fxi[i] = f(stars[[i]])
}

# mencari black hole
n_bh = which.min(fxi) # star ke berapa yang punya nilai fxi terkecil
bh = stars[[n_bh]] # definisi black hole
f_bh = fxi[n_bh] # nilai f_bh

# iterasi BHO kita mulai dari sini
for(ikang in 1:max_iter){
  # menghitung radius event horizon
  r = f_bh / sum(fxi)

  # saat ada bintang yang berjarak kurang dari r akan kita hapus
  jarak = abs(fxi - f_bh)
  n_luar = which(jarak >= r)

  # stars yang ada di n_luar 
  stars = stars[n_luar]

  # jika jumlah stars < N --> big bang lagi
  n_stars = length(stars)
  if(n_stars < N){
    # membuat bintang dan menghitung nilai fxi-nya
    for(i in (n_stars + 1):N){
        stars[[i]] = big_bang()
        fxi[i] = f(stars[[i]])
    }
  }

  # gravity rate - akan dbuat tetap
  g = runif(1,0,1.5)

  # iterasi proses penarikan bintang ke black hole
  for(j in 1:N){
    xt = stars[[j]]
    xt_new = bh + g * (xt - bh)
    xt_new_1 = xt_new %>% round(0)
    fxi[j] = f(xt_new_1)
    stars[[j]] = xt_new
  }

  # mencari black hole
  n_bh = which.min(fxi) # star ke berapa yang punya nilai fxi terkecil
  bh = stars[[n_bh]] # definisi black hole
  f_bh = fxi[n_bh] # nilai f_bh
}

stars[[n_bh]] %>% round(0)

## [1] 190  60

fxi[n_bh]

## [1] -2050000

Twitter Facebook LinkedIn

Bunch of Ideas, a little bit of Maths.

Berkenalan dengan Black Hole Optimization Algorithm

OPTIMISASI

Aplikasi Algoritma Optimisasi

BIG BANG - BLACK HOLE INSPIRED OPTIMIZATION ALGORITHM

Ilustrasi

Hal Penting dalam BHO

Gravity rate

Radius event horizon

Pseudocode

MAXIMIZING / MINIMIZING

Contoh

Contoh

PENCARIAN AKAR

Contoh Soal

OPTIMISASI

Mengubah Constrained Optimization

Contoh Soal

You May Also Enjoy

Membaca Profil Seseorang dari IG Feeds Menggunakan ChatGPT

Setting Awal Untuk Menjalankan Model Huggingface di Laptop Sendiri

Menjalankan R Studio Server di Railway.app

Math and Computational Science for Business part 2: Validasi Hipotesis dalam Sales dan Distribusi