Bunch of Ideas, a little bit of Maths.

I am mathematician doing market research and data science

8 minute read

Jika rekan-rekan membaca blog saya beberapa minggu belakangan, kalian akan menyadari bahwa ada 3 topik yang sedang rajin saya tulis, yakni:

  1. Agentic AI di R,
  2. Bayesian statistics, dan
  3. Analisa clustering.

Kali ini saya akan membahas analisa clustering dengan prinsip Bayesian. Seru kan? Saya mulai yah.

Bayesian Clustering

Bayesian clustering adalah pendekatan probabilistik untuk clustering yang menggunakan metode Bayesian untuk mengelompokkan data. Prinsip dasarnya adalah:

  • Model-based: Mengasumsikan data berasal dari campuran distribusi probabilistik.
  • Bayesian inference: Menggunakan prior dan posterior untuk estimasi parameter.
  • Uncertainty quantification: Menyediakan ukuran ketidakpastian untuk setiap cluster.

Keunggulan Bayesian clustering adalah:

  • Flexible: Dapat menangani berbagai jenis data dan struktur cluster.
  • Automatic model selection: Dapat menentukan jumlah kluster secara otomatis.
  • Uncertainty estimates: Menyediakan probabilitas keanggotaan cluster.
  • Robust: Lebih tahan terhadap noise dan outliers.

Lantas apa perbedaannya dengan K-means clustering?

Aspek K-Means Bayesian Clustering
Pendekatan Deterministik Probabilistik
Jumlah Kluster Harus ditentukan sebelumnya Dapat ditentukan otomatis
Keanggotaan Hard assignment (satu kluster) Soft assignment (probabilitas)
Asumsi Cluster berbentuk spherical dengan ukuran sama Fleksibel terhadap bentuk dan ukuran cluster
Ketidakpastian Tidak ada ukuran ketidakpastian Menyediakan posterior probabilities
Komputasi Cepat dan sederhana Lebih kompleks dan intensif
Model Selection Manual (elbow method, silhouette) Otomatis (Bayesian model comparison)
Outliers Sensitif terhadap outliers Lebih robust terhadap outliers

Secara praktis, perbedaan penggunaannya adalah sebagai berikut:

  • K-Means: Cocok untuk data yang terpisah jelas dengan bentuk spherical. Hal ini pernah saya bahas di tulisan blog yang ini. Silakan dibaca ya.
  • Bayesian: Cocok untuk data kompleks dengan overlap, ketidakpastian tinggi, atau ketika ingin mengetahui probabilitas keanggotaan.

Sekarang saya akan berikan contoh sederhana menggunakan data rekaan yang representatif. Saya akan buat sebuah data berisi dua variabel X_1 dan X_2. Saya juga definisikan masing-masing data tersebut masuk ke cluster berapa. Hal ini sebagai informasi awal bagi kita agar untuk melihat apakah ada perubahan cluster setelah dilakukan Bayesian clustering.

Berikut adalah visualisasi datanya:

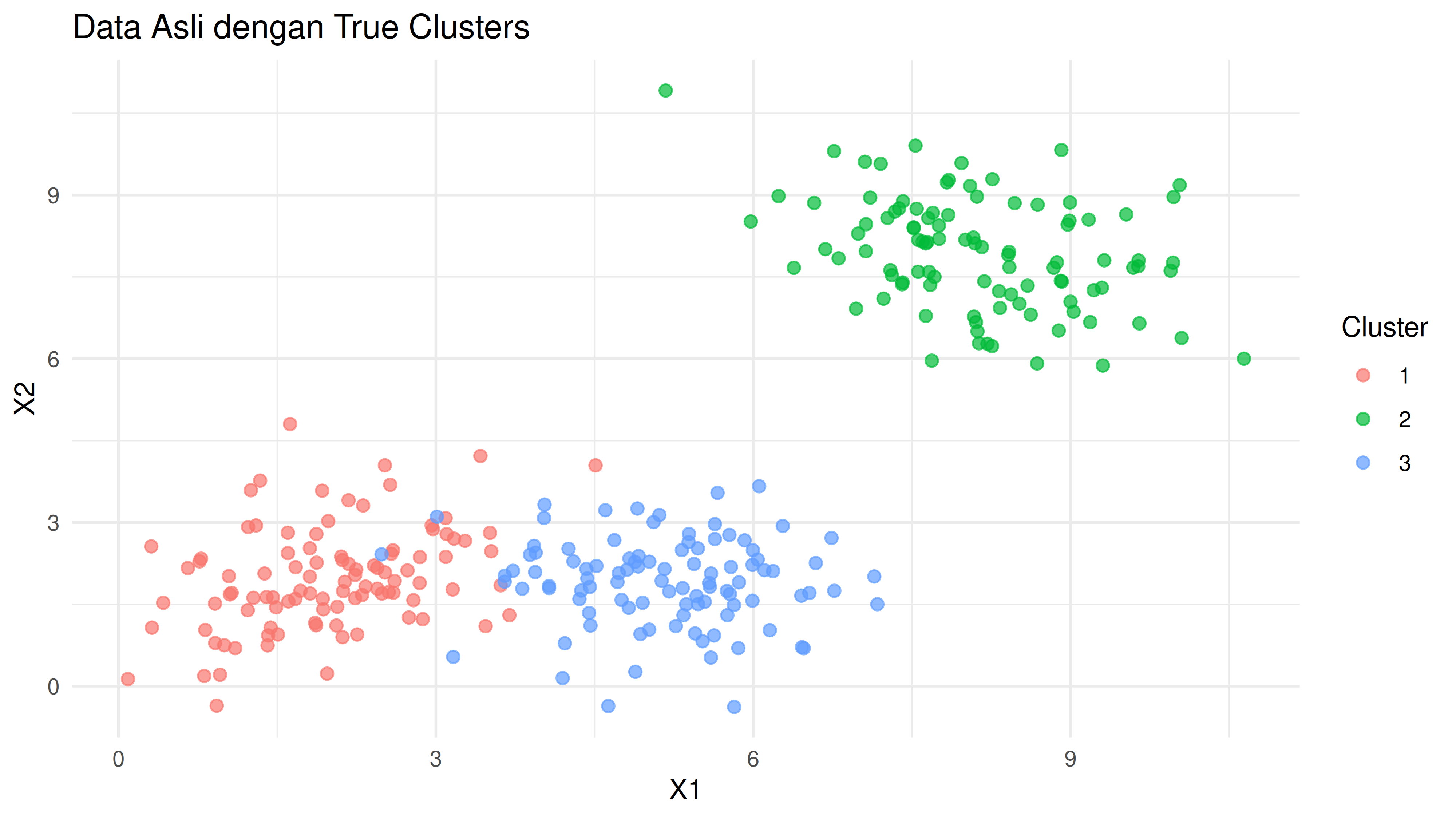
Kita bisa melihat bahwa cluster 2 benar-benar terpisah dari clusters yang lain. Ada beberapa titik data di cluster 1 dan 3 yang saling tumpang tindih.

Untuk melakukan Bayesian clustering di R, prosesnya cukup mudah. Yakni:

# Menggunakan mclust untuk Bayesian GMM
fit_mclust <- Mclust(X, G = 1:5, modelNames = "VVV")

# Hasil clustering
mclust_clusters    <- fit_mclust$classification
mclust_uncertainty <- fit_mclust$uncertainty

# Summary model
summary(fit_mclust)

---------------------------------------------------- 
Gaussian finite mixture model fitted by EM algorithm 
---------------------------------------------------- 

Mclust VVV (ellipsoidal, varying volume, shape, and orientation) model with 3
components: 

 log-likelihood   n df      BIC       ICL
      -1092.798 300 17 -2282.56 -2297.245

Clustering table:
  1   2   3 
 98 102 100

Berikut adalah visualisasi hasil clustering-nya:

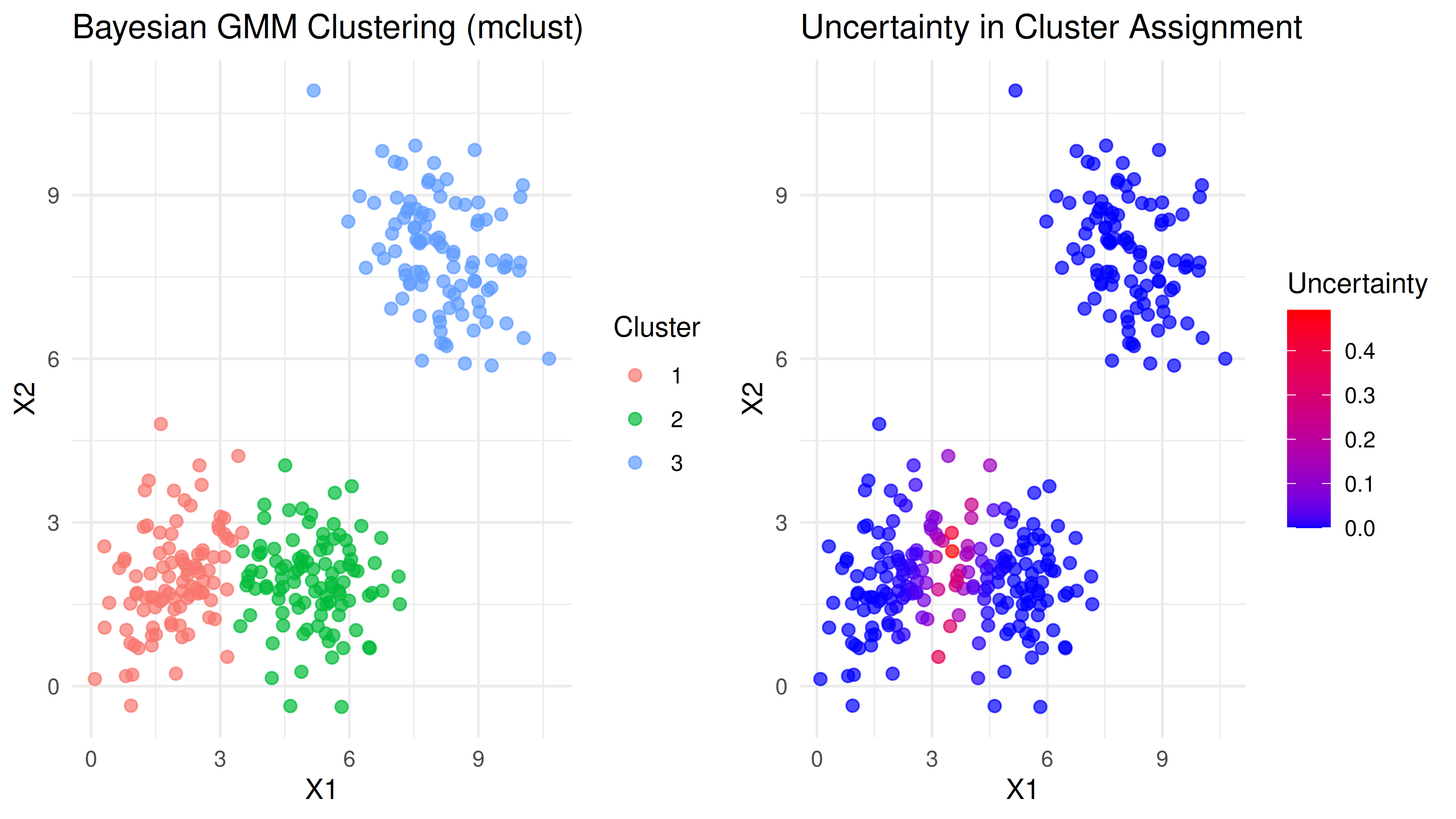
Secara visual, kita bisa melihat ada perbedaan cluster member pada dua clusters yang saling tumpang tindih. Kita juga bisa mendapatkan nilai uncertainty dari masing-masing titik data.

Sekarang, saya perlu mengevaluasi performa dari clustering-nya. Ada dua metrik evaluasi yang bisa dihitung: internal dan eksternal.

Untuk metrik internal, kita bisa menghitung BIC (Bayesian Information Criterion) untuk menentukan ada berapa banyak clusters yang pas untuk data tersebut. Nilai BIC yang lebih tinggi menunjukkan model yang lebih baik.

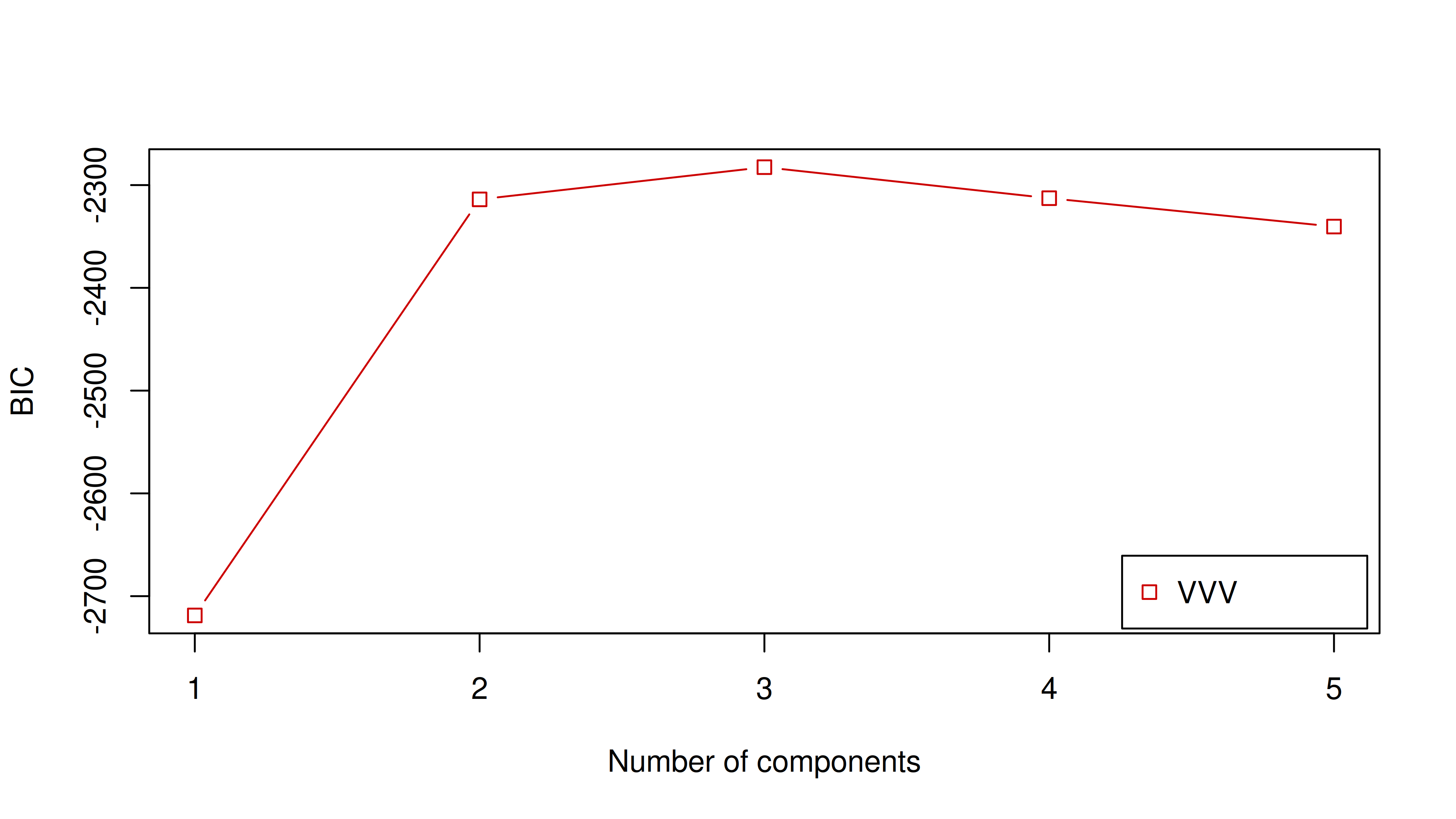
Dari grafik di atas, terlihat bahwa saat banyaknya clusters = 3 menghasilkan nilai BIC yang paling tinggi dibandingkan yang lain.

Untuk metrik eksternal, kita bisa menghitungnya dengan syarat ground truth tersedia. Pada awal saya generate data, saya sudah memberikan cluster awal. Jika clusters tersebut kita yakini sebagai ground truth, kita bisa menghitung Adjusted Rand Index (ARI).

Adjusted Rand Index: 0.923

ARI mengukur kesamaan antara clustering hasil dan ground truth. ARI > 0.8 menunjukkan hasil clustering yang sangat baik.

Di banyak kasus real, kita tidak selalu memiliki ground truth. Maka kita tidak perlu menghitung ARI. Kita bisa menghitung beberapa metrik lain seperti:

Silhouette analysis: mengukur seberapa baik setiap observasi cocok dengan cluster-nya.

library(cluster)
sil <- silhouette(fit_mclust$classification, dist(X))
cat("Mean Silhouette Width:", mean(sil[, 3]), "\n")

Mean Silhouette Width: 0.6063206

Interpretasi:

  • > 0.7: Struktur kuat.
  • 0.5 - 0.7: Struktur reasonable.
  • 0.25 - 0.5: Struktur lemah.
  • < 0.25: Tidak ada struktur.

Selain itu, kita bisa menganalisa uncertainty yang terjadi. Clustering yang baik akan menghasilkan uncertainty yang rendah. Kita bisa mendefinisikan rendah jika proporsi high uncertainty sedikit.

Pada kasus ini, kita mendapatkan:

cat("Proportion with high uncertainty (>0.1):", mean(fit_mclust$uncertainty > 0.1))

Proportion with high uncertainty (>0.1): 0.08

Ternyata hanya 0.08 persen proporsi high uncertainty dan sangat rendah.

if you find this article helpful, support this blog by clicking the ads.

You May Also Enjoy