Bunch of Ideas, a little bit of Maths.

I am mathematician doing market research and data science

18 minute read

Dalam beberapa kesempatan, saya pernah menuliskan beberapa penerapan unsupervised machine learning, yakni clustering analysis. Kali ini saya akan berikan beberapa showcases penerapan metode clustering dengan R. Setidaknya ada tiga metode clustering yang terkenal dan biasa digunakan, yakni:

  1. K-means clustering,
  2. Hierarchical clustering, dan
  3. DBScan clustering.

Mari kita bahas satu-persatu.

K-Means Clustering

K-means clustering adalah metode clustering yang paling terkenal di antara metode clustering yang lainnya. Metode ini paling cocok digunakan untuk tipe data yang berbentuk centroid atau terkumpul di suatu titik tertentu.

Algoritma pengerjaannya cukup sederhana, yakni:

  1. Kita harus menentukan terlebih dahulu berapa banyak cluster (menentukan nilai k).
  2. Penentuan nilai k bisa dilakukan dengan cara:
    • Melihat secara visual grafik yang muncul.
    • Menggunakan elbow method atau silhouette method.
  3. Hitung k-means clustering dengan nilai k yang telah diketahui.

Misalkan saya memiliki kasus-kasus sebagai berikut:

Contoh Kasus I

# import data
df = read.csv("~/Live-Session-Nutrifood-R/LEFO Market Research/LEFO MR 2023/Unsupervised/k means/compact disks.csv") %>% 
     janitor::clean_names() %>%
     select(-x) %>%
     rename(x = x_2)

# kita bikin visualisasinya terlebih dahulu
plt = 
  df %>%
  ggplot(aes(x,y)) +
  geom_point() + 
  coord_equal()
plt

Jika melihat langsung data di atas, kita sudah bisa pastikan bahwa ada k = 4 buah cluster.

Namun bagaimana jika kita gunakan elbow method dan silhouette method untuk menentukan berapa banyaknya k?

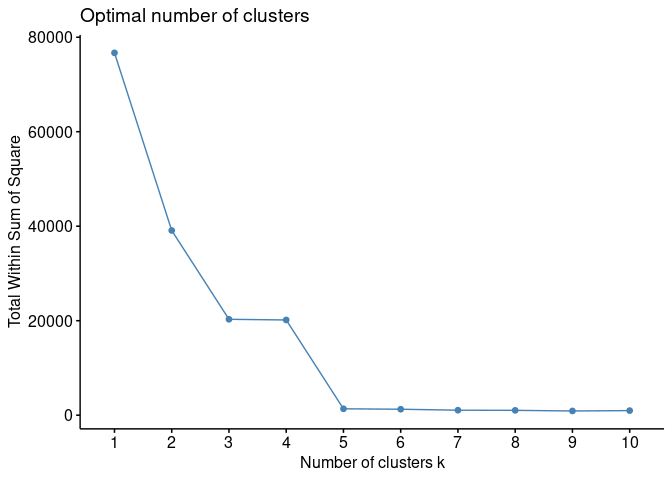
Elbow Method

elbow = fviz_nbclust(df, kmeans, method = "wss")
plot(elbow)

Silhouette Method

siluet = fviz_nbclust(df, kmeans, method = "silhouette")
plot(siluet)

Kesimpulan Sementara

Kita bisa melihat bahwa nilai k hasil elbow method dan silhouette method tidak sama dengan 4. Hasil ini berpotensi menjadi miss leading. Akan saya berikan visualnya dengan berbagai nilai k yang kita sudah ketahui dari analisa sebelumnya.

Jika k=5

# k-means clustering
final = kmeans(df, 5, nstart = 25)

# center dari masing-masing cluster
final$centers

##             x           y
## 1  0.04097999  9.98130971
## 2 10.04097999  9.98130971
## 3  0.04097999 -0.01869029
## 4 10.50025161 -0.39974068
## 5  9.53552463  0.40067802

# save hasil cluster ke data awal
data_kmeans = df
data_kmeans$cluster = final$cluster

# berapa banyak isi dari cluster
table(data_kmeans$cluster)

## 
##   1   2   3   4   5 
## 376 376 376 197 179

plt = 
  data_kmeans %>%
  ggplot(aes(x,y)) +
  geom_point(aes(color = as.factor(cluster))) +
  coord_equal()
plt

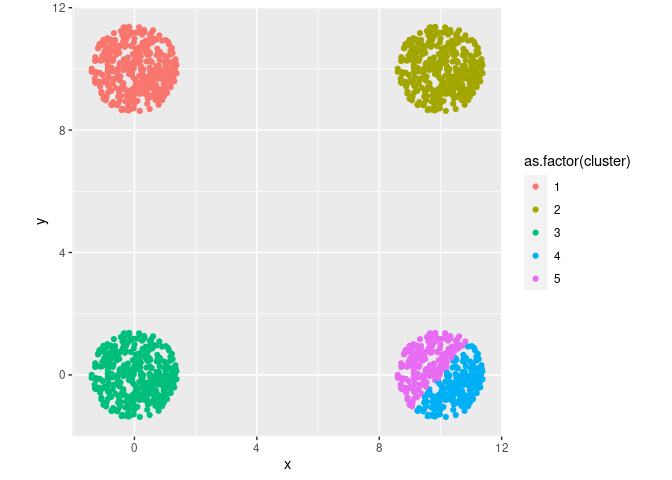
Jika k=6

# k-means clustering
final = kmeans(df, 6, nstart = 25)

# center dari masing-masing cluster
final$centers

##             x           y
## 1  0.04097999 -0.01869029
## 2 10.50025161  9.60025932
## 3 10.50025161 -0.39974068
## 4  9.53552463  0.40067802
## 5  9.53552463 10.40067802
## 6  0.04097999  9.98130971

# save hasil cluster ke data awal
data_kmeans = df
data_kmeans$cluster = final$cluster

# berapa banyak isi dari cluster
table(data_kmeans$cluster)

## 
##   1   2   3   4   5   6 
## 376 197 197 179 179 376

plt = 
  data_kmeans %>%
  ggplot(aes(x,y)) +
  geom_point(aes(color = as.factor(cluster))) +
  coord_equal()
plt

Mari kita bandingkan dengan jawaban yang benar.

Jawaban yang Benar

Seharusnya k=4.

# k-means clustering
final = kmeans(df, 4, nstart = 25)

# center dari masing-masing cluster
final$centers

##             x           y
## 1  0.04097999 -0.01869029
## 2 10.04097999  9.98130971
## 3 10.04097999 -0.01869029
## 4  0.04097999  9.98130971

# save hasil cluster ke data awal
data_kmeans = df
data_kmeans$cluster = final$cluster

# berapa banyak isi dari cluster
table(data_kmeans$cluster)

## 
##   1   2   3   4 
## 376 376 376 376

plt = 
  data_kmeans %>%
  ggplot(aes(x,y)) +
  geom_point(aes(color = as.factor(cluster))) +
  coord_equal()
plt

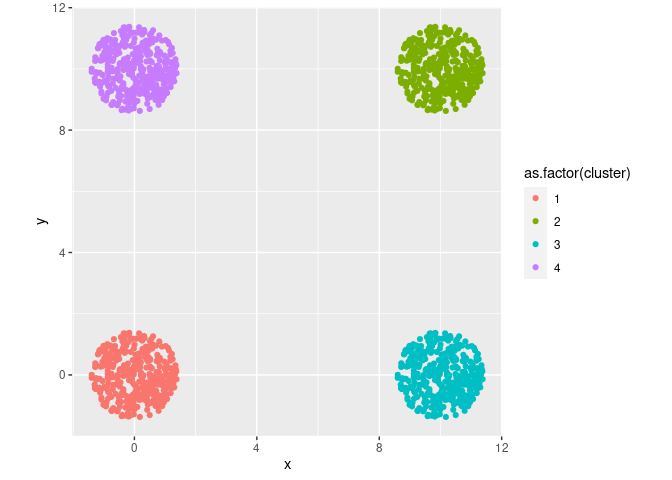
Lantas bagaimana jika kita tidak bisa menentukan banyaknya k secara visual dan hanya bisa mengandalkan elbow dan silhouette method?

Sabar, saya akan menjawabnya pada tulisan selanjutnya.

Contoh Kasus II

Kita akan beralih ke contoh selanjutnya seperti ini:

# import data
df = read.csv("~/Live-Session-Nutrifood-R/LEFO Market Research/LEFO MR 2023/Unsupervised/k means/dual disks.csv") %>% 
     janitor::clean_names() %>%
     select(-x) %>%
     rename(x = x_2)

# kita bikin visualisasinya terlebih dahulu
plt = 
  df %>%
  ggplot(aes(x,y)) +
  geom_point() +
  coord_equal()
plt

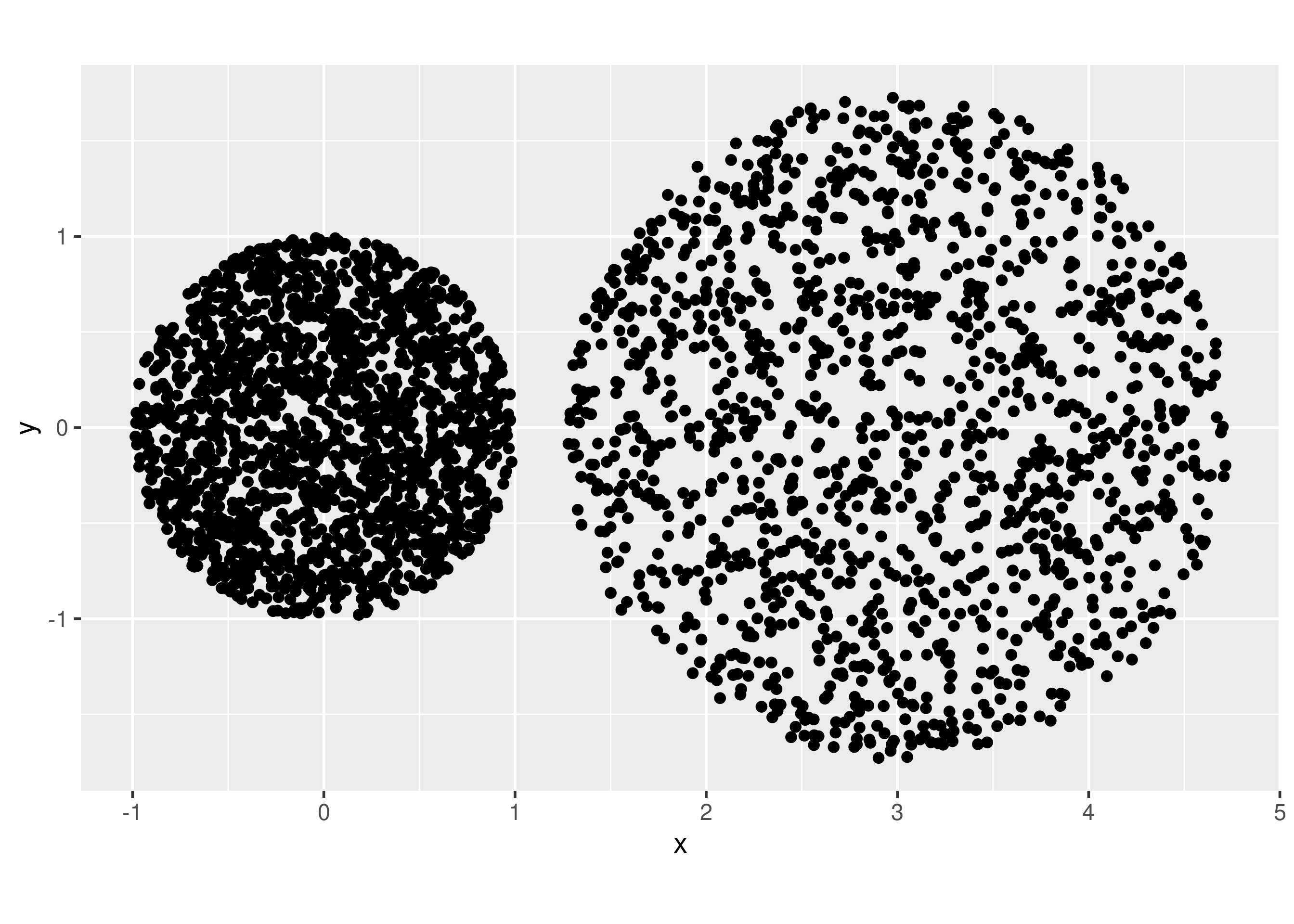
Jika melihat langsung data di atas, kita sudah bisa pastikan bahwa ada k = 2 buah cluster.

Namun bagaimana jika kita gunakan elbow method dan silhouette method untuk menentukan berapa banyaknya k?

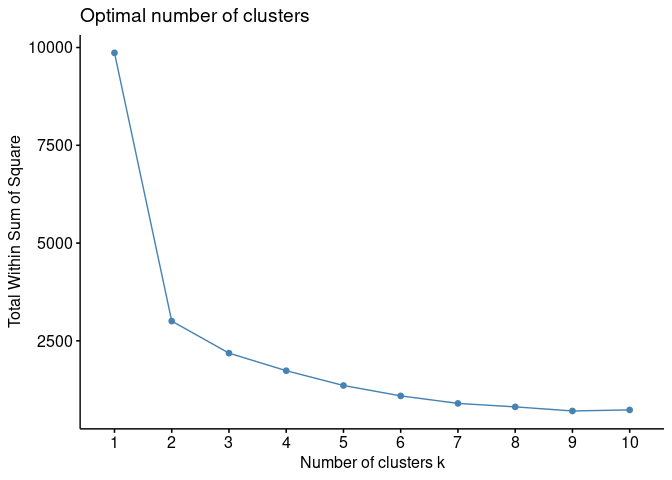
Elbow Method

elbow = fviz_nbclust(df, kmeans, method = "wss")
plot(elbow)

Silhouette Method

siluet = fviz_nbclust(df, kmeans, method = "silhouette")
plot(siluet)

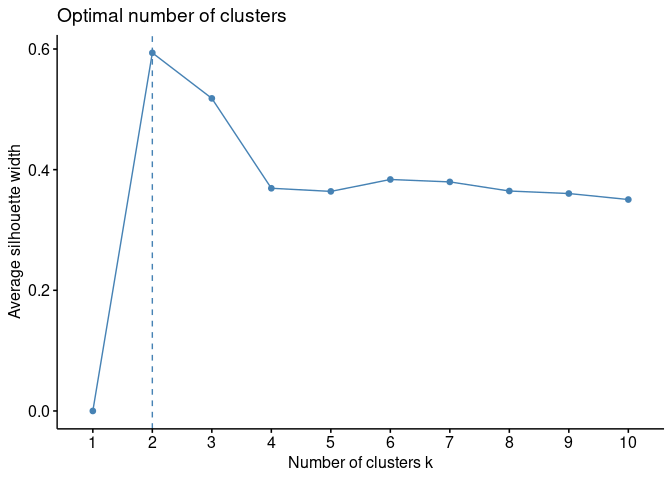
Kedua metode tersebut konklusif menyatakan k=2. Hal ini juga sama dengan temuan secara visual. Kita akan masukkan nilai k ke algoritma dan buat visualisasinya kembali:

# k-means clustering
final = kmeans(df, 2, nstart = 25)

# center dari masing-masing cluster
final$centers

##            x           y
## 1 0.04054186 0.003287305
## 2 3.01638486 0.018651232

# save hasil cluster ke data awal
data_kmeans = df
data_kmeans$cluster = final$cluster

# berapa banyak isi dari cluster
table(data_kmeans$cluster)

## 
##    1    2 
## 1763 1381

plt = 
  data_kmeans %>%
  ggplot(aes(x,y)) +
  geom_point(aes(color = as.factor(cluster))) +
  coord_equal()
plt

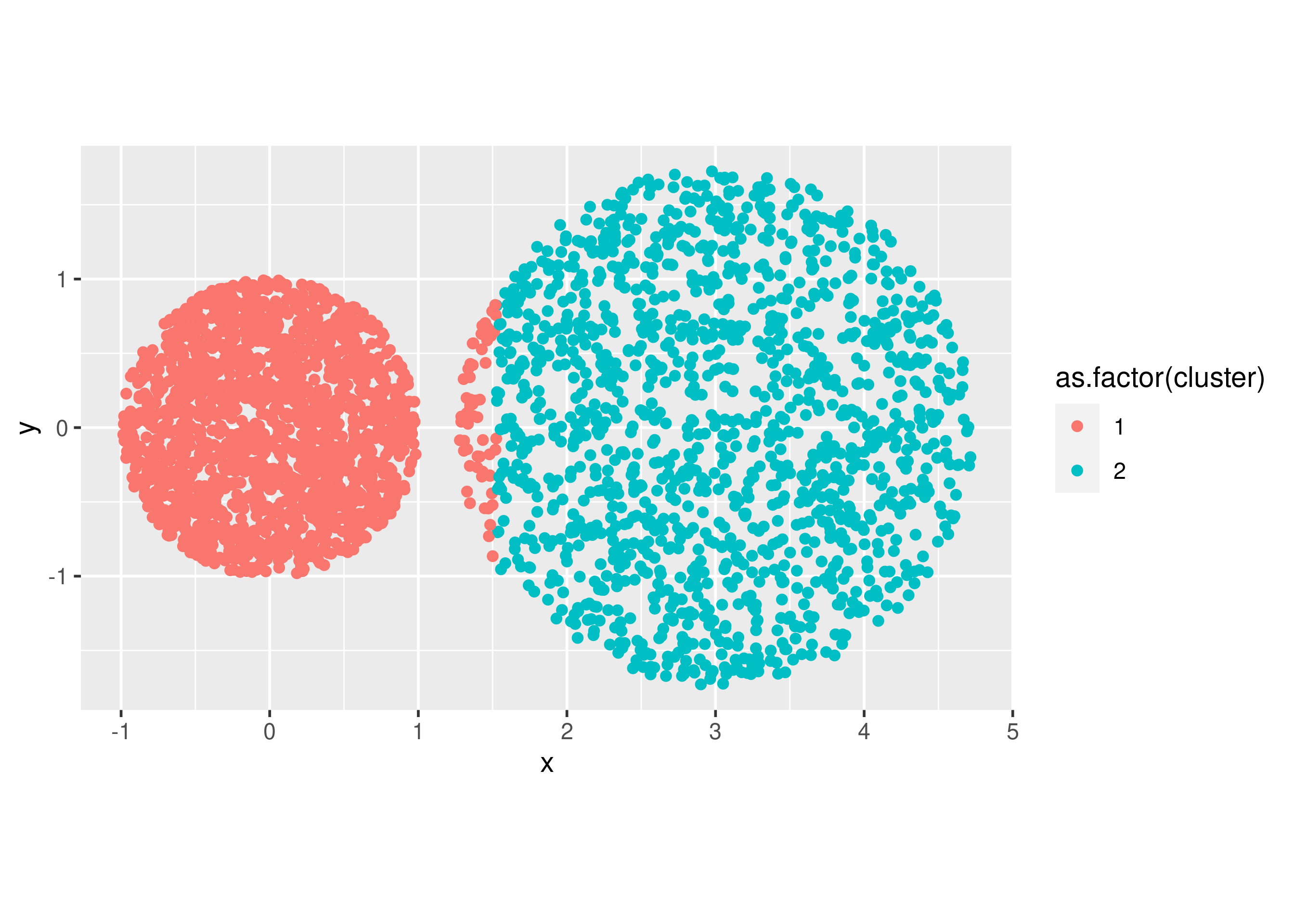
Terlihat bahwa ada beberapa titik data yang overlap masuk ke cluster lainnya. Hal ini seharusnya tidak boleh terjadi. Sehingga bisa kita simpulkan sementara bahwa tidak semua bentuk data yang centroid bisa digunakan k-means clustering.

Hierarchical Clustering

Metode clustering selanjutnya adalah hierarchical clustering. Algoritmanya sederhana, yakni:

  1. Dari sekumpulan data yang ada, hitung jarak antar titik data.
  2. Buat cluster dari dua titik yang memiliki jarak terdekat tersebut.
  3. Hitung kembali jarak antar titik data dengan cluster yang terbentuk dijadikan satu kesatuan titik.
  4. Ulangi langkahnya hingga semua titik berhasil dikelompokkan.

Hal yang krusial pada metode ini adalah penentuan jarak suatu cluster dengan titik (atau cluster lainnya). Kita bisa pilih apakah akan menggunakan metode:

  1. Single link,
  2. Max,
  3. Average, dll.

Misalkan saya punya contoh sebagai berikut:

Contoh I

rm(list=ls())
df = read.csv("~/Live-Session-Nutrifood-R/LEFO Market Research/LEFO MR 2023/Unsupervised/hierarchical/donat.csv") %>% 
     janitor::clean_names() %>%
     select(x_2,y) %>%
     rename(x = x_2)

# membuat grafik
plt = 
  df %>%
  ggplot(aes(x,y)) +
  geom_point() +
  coord_equal()
plt


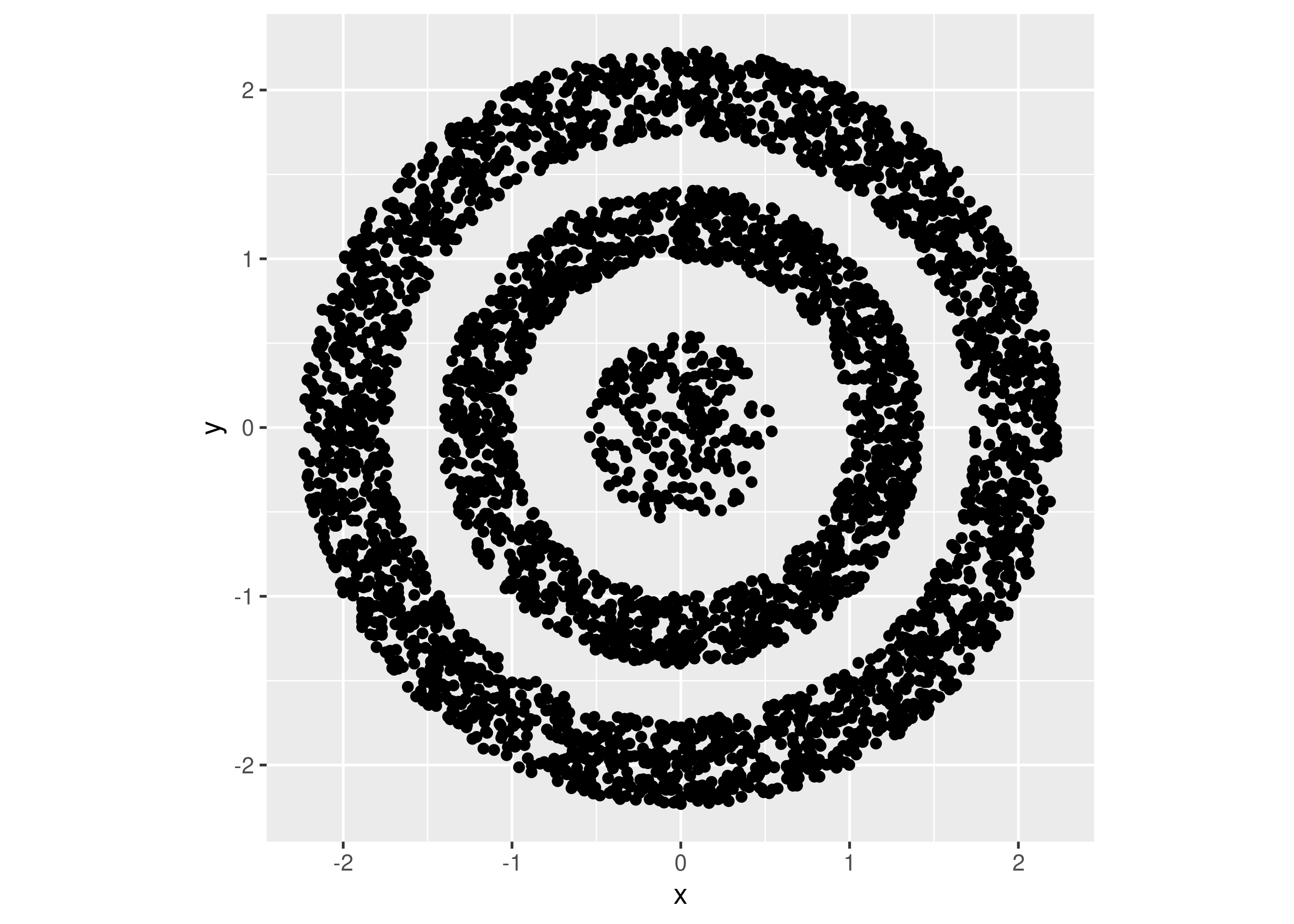
# Finding distance matrix
distance_mat = dist(df, method = 'euclidean')

Secara visual, kita bisa simpulkan ada 3 buah cluster yang ada pada data di atas. Metode perhitungan mana yang bisa memberikan hasil yang terbaik?

Mari kita lihat satu-persatu:

Perhitungan dengan metode single link.

# Fitting Hierarchical clustering Model
set.seed(240)  # Setting seed
Hierar_cl = hclust(distance_mat, method = "single")

plot(Hierar_cl)

# Pemecahan menjadi 3 cluster
fit = cutree(Hierar_cl, k = 3)
table(fit)

## fit
##    1    2    3 
##  229 1560 2541

plot(Hierar_cl)
rect.hclust(Hierar_cl, k = 3, border = "red")


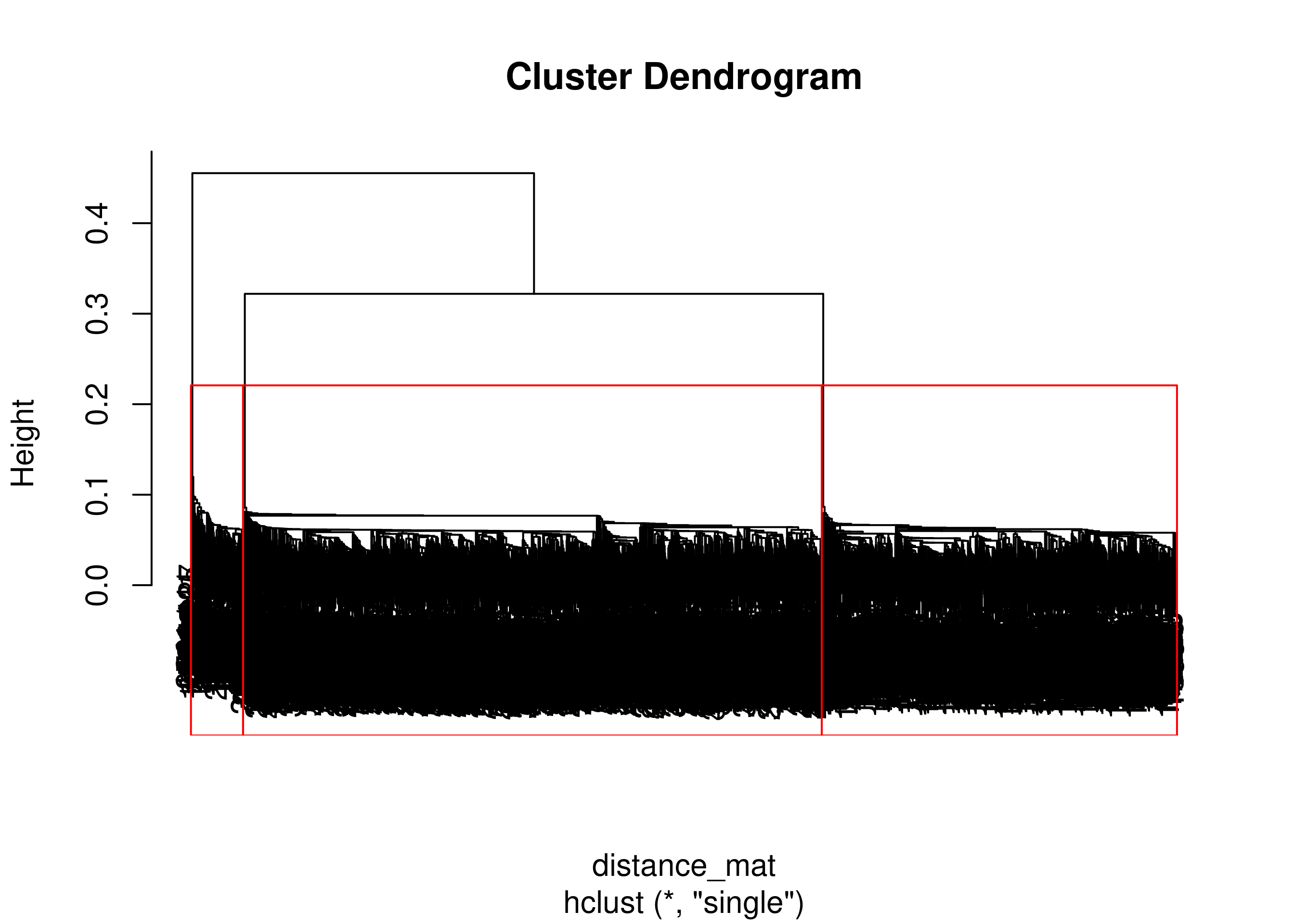
# save hasil cluster ke data awal
data_hc = df
data_hc$cluster = fit

# berapa banyak isi dari cluster
hie_plot = 
  data_hc %>%
  ggplot(aes(x,y,color = as.factor(cluster))) +
  geom_point() +
  coord_equal()
hie_plot

Max / Complete Link

Perhitungan dengan max atau complete link.

# Fitting Hierarchical clustering Model
set.seed(240)  # Setting seed
Hierar_cl = hclust(distance_mat, method = "complete")

plot(Hierar_cl)

# Pemecahan menjadi 3 cluster
fit = cutree(Hierar_cl, k = 6)
table(fit)

## fit
##   1   2   3   4   5   6 
## 767 824 814 594 834 497

plot(Hierar_cl)
rect.hclust(Hierar_cl, k = 6, border = "red")


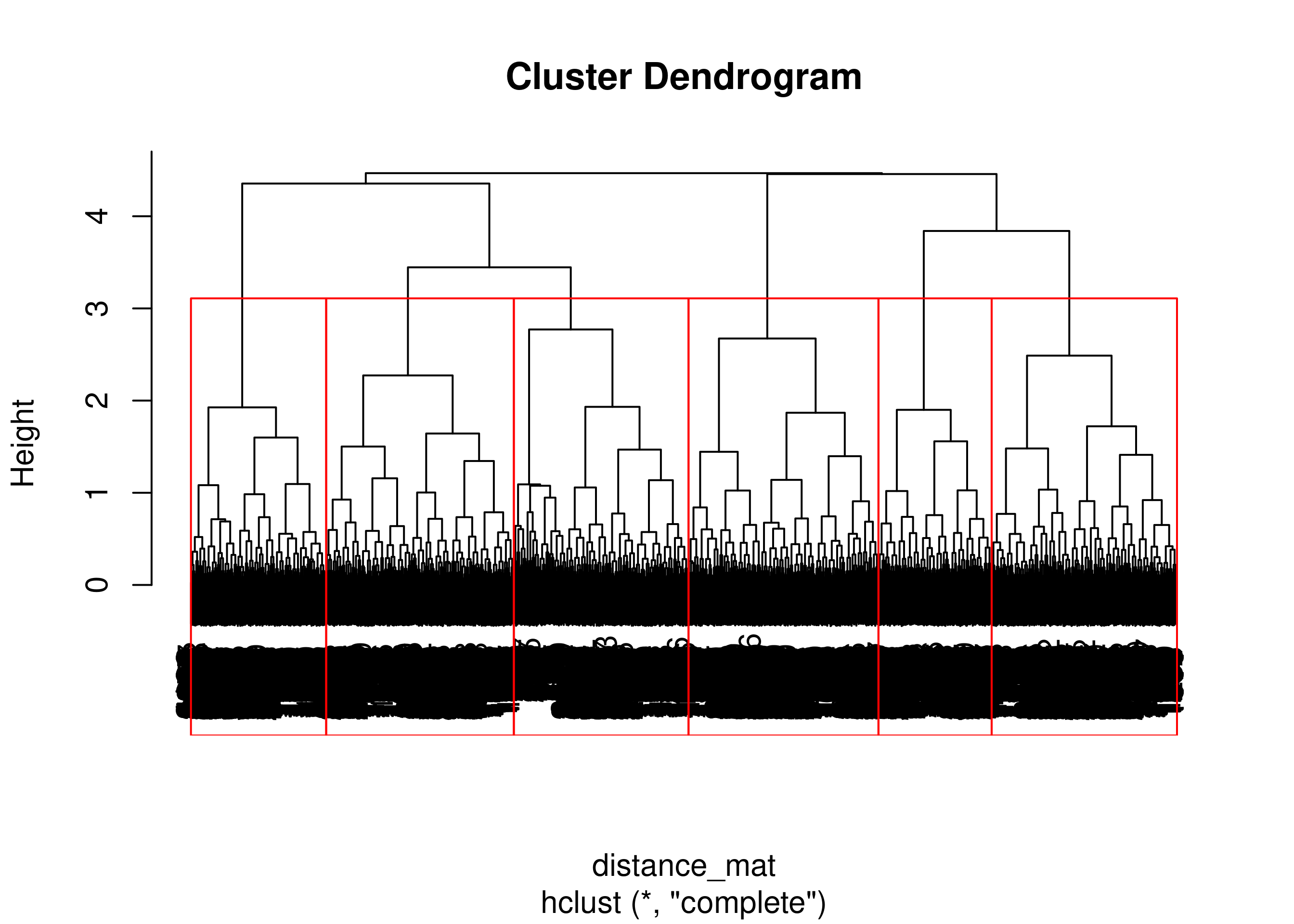
# save hasil cluster ke data awal
data_hc = df
data_hc$cluster = fit

# berapa banyak isi dari cluster
hie_plot = 
  data_hc %>%
  ggplot(aes(x,y,color = as.factor(cluster))) +
  geom_point() +
  coord_equal()
hie_plot

Perhitungan dengan average link.

# Fitting Hierarchical clustering Model
set.seed(240)  # Setting seed
Hierar_cl = hclust(distance_mat, method = "average")

plot(Hierar_cl)

# Pemecahan menjadi 3 cluster
fit = cutree(Hierar_cl, k = 4)
table(fit)

## fit
##    1    2    3    4 
## 1632 1168  732  798

plot(Hierar_cl)
rect.hclust(Hierar_cl, k = 4, border = "red")


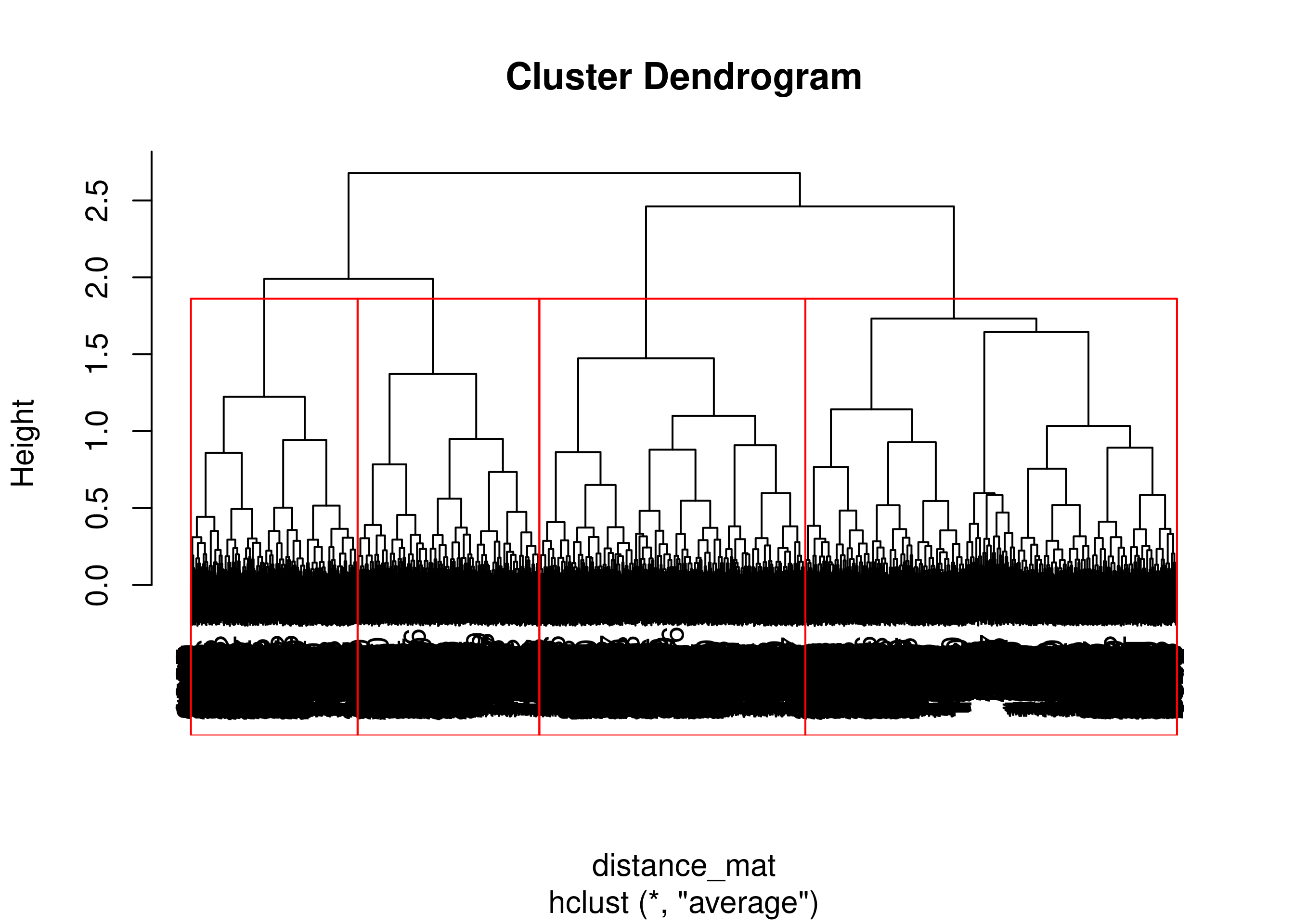
# save hasil cluster ke data awal
data_hc = df
data_hc$cluster = fit

# berapa banyak isi dari cluster
hie_plot = 
  data_hc %>%
  ggplot(aes(x,y,color = as.factor(cluster))) +
  geom_point() +
  coord_equal()
hie_plot

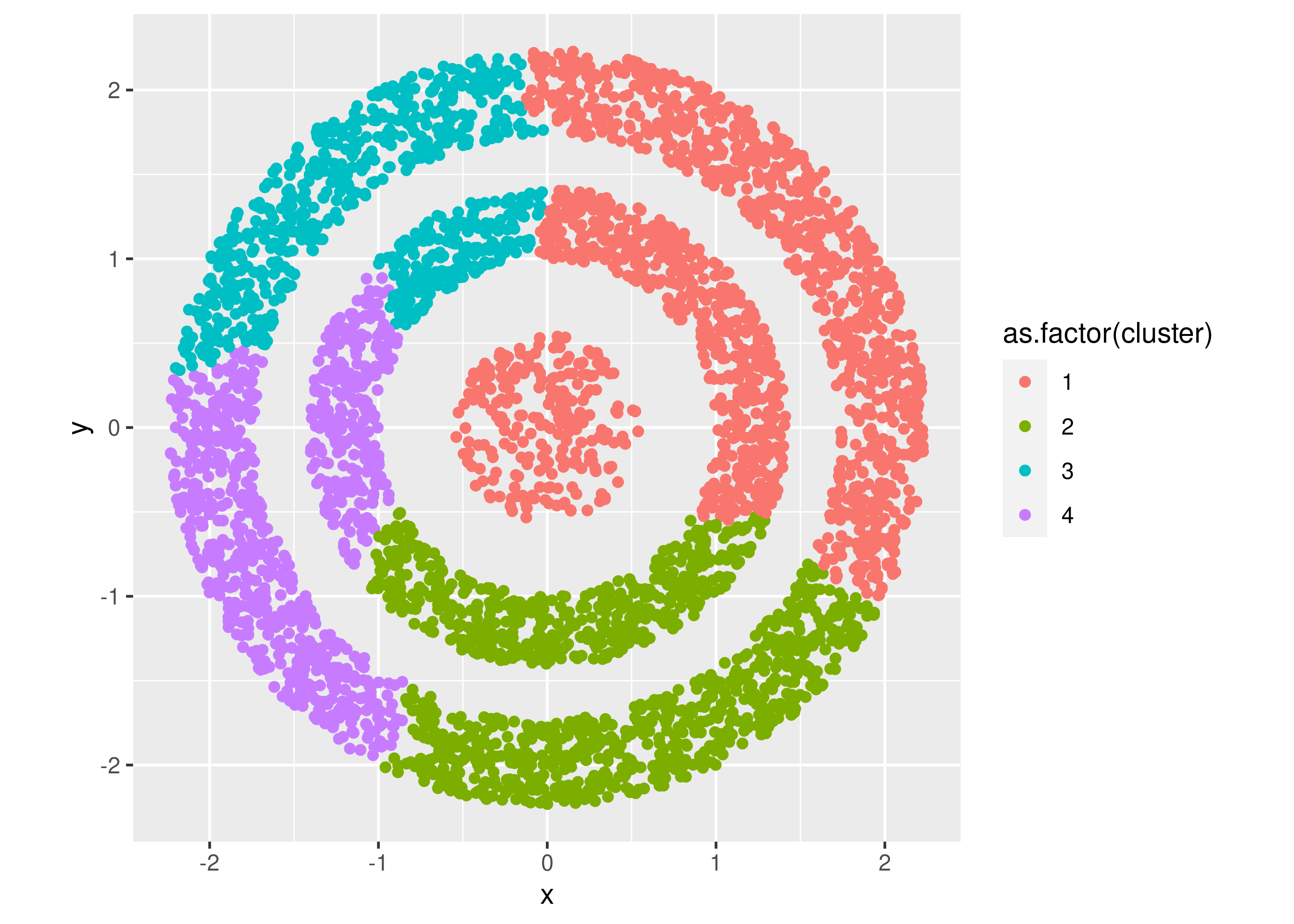
Kesimpulan

Untuk kasus ini, perhitungan dengan metode single link menghasilkan hasil cluster yang terbaik.

Contoh II

Mari kita lihat kasus berikut seperti ini:

rm(list=ls())
df = read.csv("~/Live-Session-Nutrifood-R/LEFO Market Research/LEFO MR 2023/Unsupervised/hierarchical/hi.csv") %>% 
     janitor::clean_names() %>%
     select(x_2,y) %>%
     rename(x = x_2)

# membuat grafik
plt = 
  df %>%
  ggplot(aes(x,y)) +
  geom_point() +
  coord_equal()
plt


# Finding distance matrix
distance_mat = dist(df, method = 'euclidean')

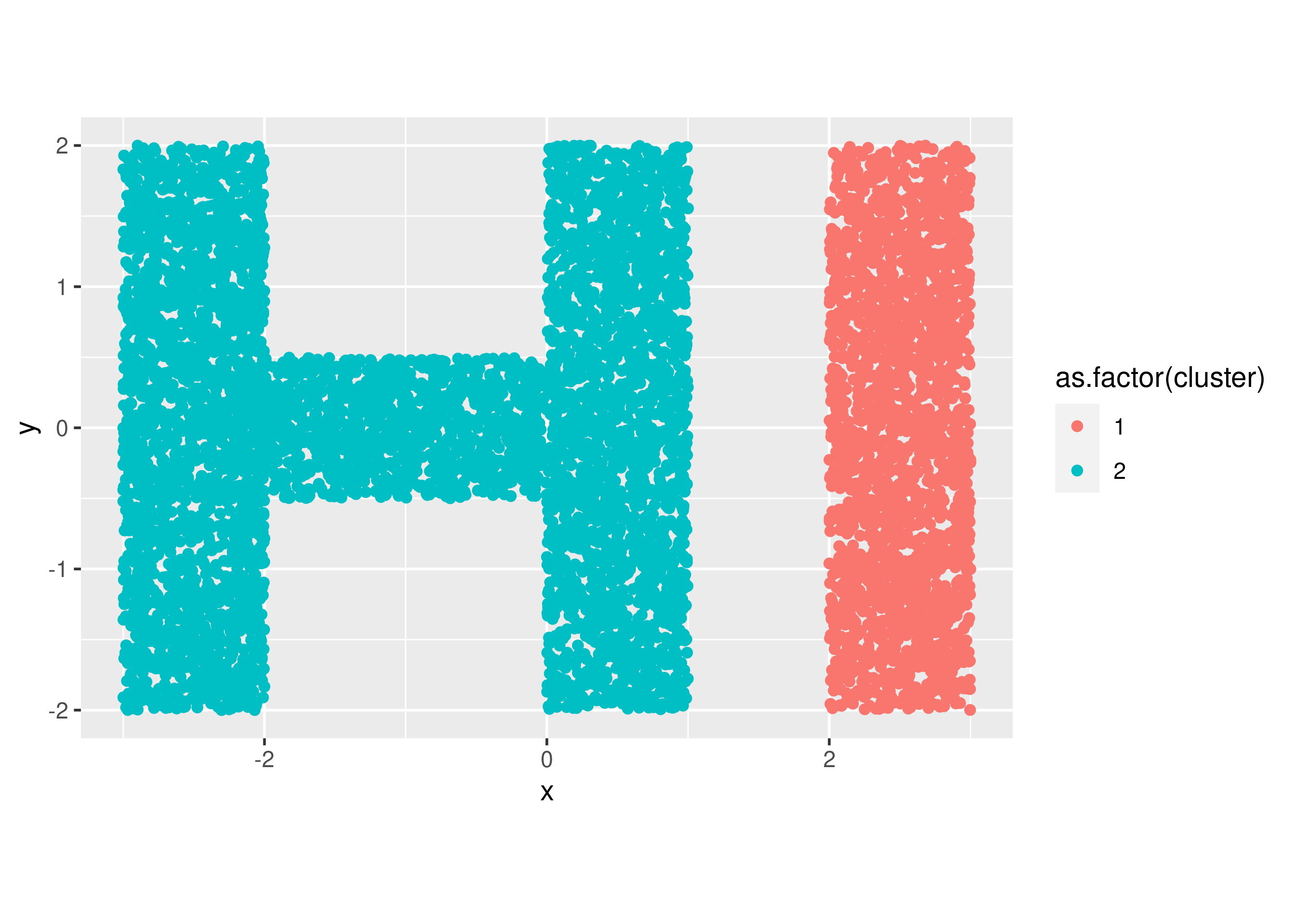
Pada kasus ini, terlihat ada dua buah cluster. Saya pun langsung hanya akan menggunakan metode single link pada perhitungannya.

# Fitting Hierarchical clustering Model
set.seed(240)  # Setting seed
Hierar_cl = hclust(distance_mat, method = "single")

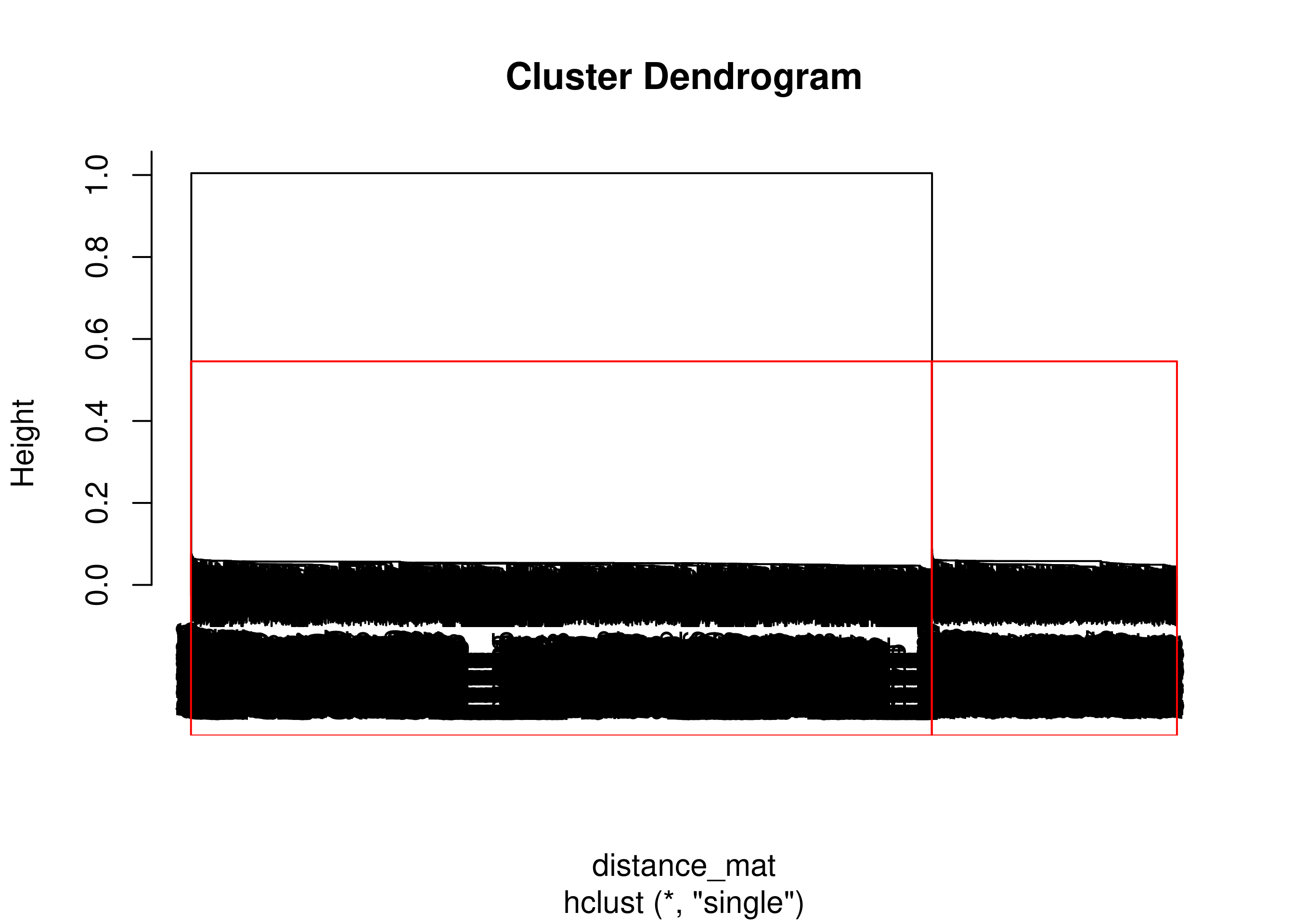
plot(Hierar_cl)

# Pemecahan menjadi 2 cluster
fit = cutree(Hierar_cl, k = 2)
table(fit)

## fit
##    1    2 
## 2223 6717

plot(Hierar_cl)
rect.hclust(Hierar_cl, k = 2, border = "red")


# save hasil cluster ke data awal
data_hc = df
data_hc$cluster = fit

# berapa banyak isi dari cluster
hie_plot = 
  data_hc %>%
  ggplot(aes(x,y,color = as.factor(cluster))) +
  geom_point() +
  coord_equal()
hie_plot

DBScan

Metode clustering yang terakhir ini merupakan metode perhitungan density based. Sangat berguna untuk data yang memiliki noise. Misalkan saya memiliki contoh sebagai berikut:

Contoh I

rm(list=ls())

# ambil data
df = read.csv("~/Live-Session-Nutrifood-R/LEFO Market Research/LEFO MR 2023/Unsupervised/dbscan/donat density.csv") %>%
     janitor::clean_names() %>% 
     select(-x) %>% rename(x = x_2)

df |>
  ggplot(aes(x,y)) +
  geom_point() +
  coord_equal()

Bagaimana agar kita bisa mendapatkan cluster yang terbaik?

Langkah pertama adalah mendefinisikan terlebih dahulu k Nearest Neighbor untuk membantu kita menentukan standar density suatu cluster. Berikutnya adalah menentukan h yang teroptimal saat grafik NN distance-nya meningkat tinggi.

Sebaga contoh, saya akan ambil nilai 30 sebagai patokan nearest neighbor.

dbscan::kNNdistplot(df, k = 30)
abline(h = .25, lty = 2, col = "red")

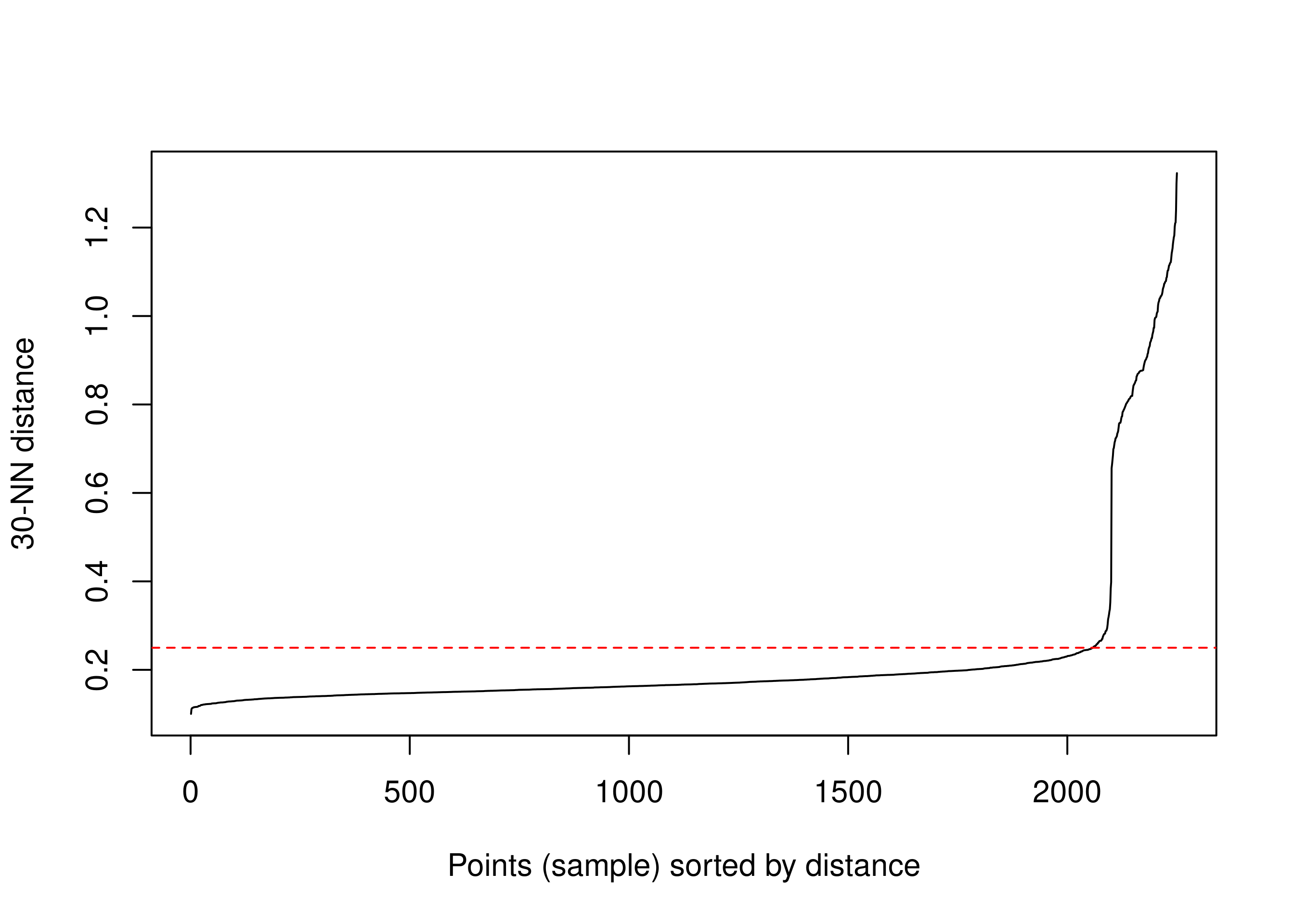
Kita akan pilih h = .25.

# membuat clustering DBScan
# set sed agar reproducible
set.seed(20921004)
Dbscan_cl = dbscan(df, eps = 0.25, minPts = 5)

# menambahkan cluster ke dalam dataset
df$cluster_new = Dbscan_cl$cluster

df |>
  ggplot(aes(x,y)) +
  geom_point(aes(color = as.factor(cluster_new)),
             size = 2) +
  coord_equal()

You May Also Enjoy

Geocoding di R Menggunakan tidygeocoder

7 minute read

Di blog ini saya sudah menuliskan berbagai macam metode dan teknik pengambilan data longlat dari alamat (vice versa). Istilah kerennya itu geocoding.