Belajar Membuat Model Regresi Linear - part 1

Kita pasti sudah sering mendengar, melihat, bahkan membuat model regresi linear . Bagi saya pribadi, metode linear curve fitting yang satu ini adalah salah satu metode statistik yang sering ditanyakan oleh banyak rekan kerja. Pertama kali saya mengenal regresi linear adalah pada saat kuliah Statistika Matematika pada tingkat 3 dulu di S1.

Setidaknya saya pernah menulis tiga posts terkait regresi linear:

1. Bagaimana membuat model regresi linear di R dan menguji asumsinya di sini.
2. Aplikasi regresi linear pada perhitungan price elasticity di sini.
3. Menentukan apa yang berpengaruh terhadap kebahagiaan di suatu negara berdasarkan World Happiness Index di sini.

Tapi belum ada sama sekali tulisan yang menjelaskan bagaimana cara menentukan nilai a dan b pada persamaan regresi linear tersebut.

Nah, kali ini saya akan menjelaskan bagaimana cara kita menentukan nilai dan pada persamaan regresi .

---

Misalkan saya memiliki pasang data yang akan saya buat menjadi persamaan .

Cita-cita saya adalah memiliki persamaan yang dekat dengan aslinya sehingga menghasilkan prediksi yang akurat.

Misalkan saya definisikan error sebagai:

di mana adalah jarak antara hasil prediksi terhadap nilai real .

Saya bisa menuliskan:

Kita substitusikan kembali nilai ke definisi error, sehingga:

---

Ingat kembali bahwa tujuan mulia saya adalah meminimumkan error. Untuk itu perlu nilai dan yang tepat. Oleh karena semua data diketahui, maka kita bisa melakukan turunan parsial terhadap dan yang memenuhi:

Kita dapatkan:

atau bisa ditulis sebagai:

Kita juga dapatkan:

atau bisa ditulis sebagai:

---

Nah, kedua bentuk persamaan terakhir bisa saya tuliskan dalam bentuk matriks sebagai berikut:

Oleh karena bisa dihitung dari data, maka kita bisa tuliskan bentuk di atas menjadi bentuk . Jika matriks memiliki invers, artinya nilai a dan b bisa kita hitung.

---

Sekarang kita akan coba membuat persamaan regresi dari data tertentu berdasarkan persamaan di atas tanpa menggunakan function lm() dari base-nya R.

Misalkan saya punya data sebagai berikut:

##  [1] 3.5 6.1 4.1 5.6 4.7 7.9 7.8 4.4 6.2 5.0

##  [1] 3.5 2.2 3.2 2.5 2.9 1.3 1.3 3.1 2.2 2.8

Jika dibuat dalam bentuk scatter plot:

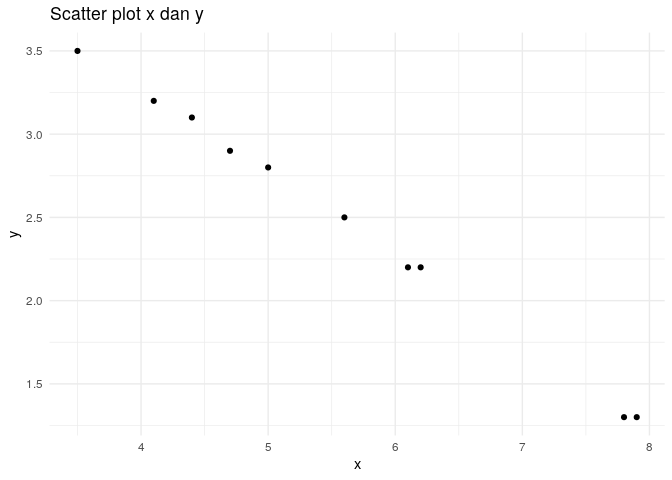
Untuk membuat persamaan regresinya, kita cukup hitung:

• 55.3
• 325.77
• 128.11
• 25

Lalu saya akan buat matriks berikut:

##      [,1]   [,2]
## [1,] 10.0  55.30
## [2,] 55.3 325.77

dan membuat vector berikut:

## [1]  25.00 128.11

Untuk mencari konstantanya, saya cukup lakukan , yakni:

solve(A) %*% d

##            [,1]
## [1,]  5.3091879
## [2,] -0.5079906

Kita dapatkan formulanya sebagai berikut:

y = -0.5079906 x + 5.3091879

Salah satu insight yang bisa kita dapatkan adalah:

Ternyata masalah curve fitting yang sering dimasukkan ke dalam statistika justru diselesaikan secara aljabar.

Mari kita bandingkan nilainya dengan base dari R sebagai berikut:

lm(y~x)

## 
## Call:
## lm(formula = y ~ x)
## 
## Coefficients:
## (Intercept)            x  
##       5.309       -0.508

Terlihat jelas bahwa hasil antara algoritma bikininan sendiri vs base R memiliki hasil yang serupa.

---

What’s Next?

Lantas apa sih gunanya membuat algoritma sendiri padahal di R sudah ada function untuk melakukan regresi?

Hal ini akan berguna saat kita hendak melakukan kustomisasi terhadap fungsi regresi yang kita buat. Contohnya adalah saat kita hendak melakukan regresi linear multi peubah, regresi polinom, regresi eksponensial, dan lain sebagainya. Saya akan menjelaskannya pada post berikutnya yah.

---

if you find this article helpful, support this blog by clicking the ads.