Coupon Collector’s Problem

Sudah membereskan empat puzzles sebelumnya? Kini saya akan membahas suatu puzzle yang sering kita lihat dan mungkin pernah kita alami di kehidupan sehari - hari.

Judulnya: Coupon collector’s problem.

---

Begini ceritanya:

Suatu perusahaan minuman soda botolan membuat sayembara. Mereka menaruh empat kupon dibalik tutup botolnya, yakni: A, B, C, dan D. Barangsiapa yang bisa mengumpulkan keempat kuponnya, akan diberikan hadiah uang sebesar 1.000 USD.

Dengan asumsi setiap kupon terdistribusi merata di pasar, harus berapa banyak botol yang kita beli agar bisa mendapatkan empat kupon tersebut?

---

Bagaimana cara menjawabnya?

Jika keempat kupon tersebut terdistribusi merata, artinya masing-masing kupon memiliki proporsi yang sama, yakni 1/4.

Mari kita lakukan kembali simulasi Monte Carlo untuk mencari harus beraa botol yang dibeli sehingga keempat kupon tersebut terkumpul!

Kali ini, saya akan lakukan iterasi hingga 9.000 kali yah.

# Coupon collector's problem
# Misal harus dapet tutup botol lengkap A-B-C-D
# Equal probabilities

tutup_botol = function(){
  sample(c(1:4),1,replace = T)
}

beli_botol = function(){
  punya = c()
  while(length(unique(punya))<4){
    punya = c(punya,tutup_botol())
  }
  length(punya)
}

iter = 9000 #mau berapa x iterasi?
berapa_x_transaksi = replicate(iter,beli_botol())

mean(berapa_x_transaksi)

## [1] 8.378778

Ternyata dibutuhkan rata-rata sekitar 8 buah botol agar kita bisa mendapatkan ke empat kupon tersebut. Rata-rata di sini adalah expected value untuk mendapatkan empat kupon.

Kalau saya buat grafik cumulative probability-nya, jadinya seperti ini:

---

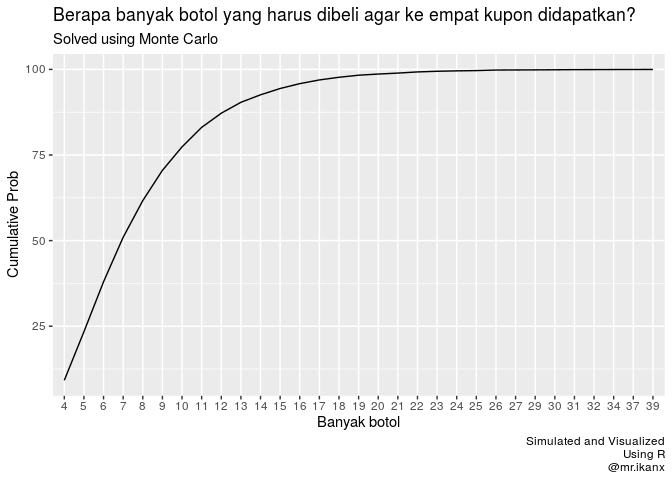
So, kalau dipikir-pikir lagi, perusahaan ini berhasil membuat setiap konsumennya (setidaknya) membeli delapan buah botol sampai semua kupon itu berhasil didapatkan.

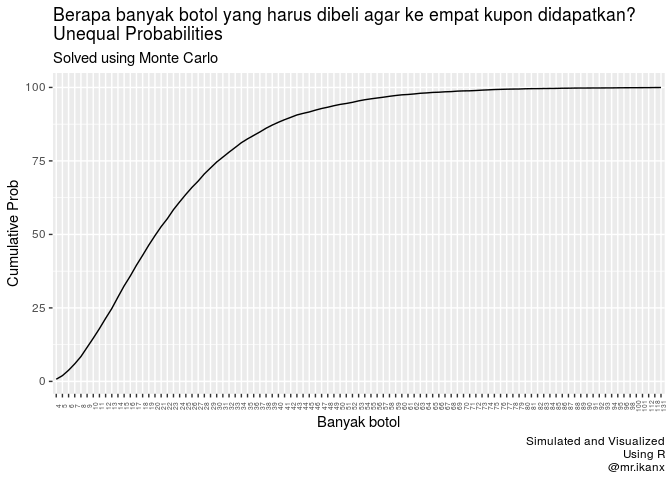
Jika proporsi masing-masing kupon tidak sama, misal ada yang lebih kecil atau besar dibanding yang lain, maka bisa dipastikan expected value-nya akan berubah menjadi lebih besar.

Contoh:

Kupon A lebih mudah ditemukan dibandingkan kupon B, C, dan D.

• A ~ 76.9%
• B+C+D ~ 23% (ketiganya proporsional)

Maka didapatkan expected value sebesar:

## [1] 23.92133