Optimization Story: Sport Science - Menentukan Konfigurasi Pelari Estafet dengan Simulasi Monte Carlo

Tulisan ini masih kelanjutan dari tulisan saya sebelumnya terkait penentuan konfigurasi pelari estafet dalam suatu perlombaan.

Saya menerima beberapa pesan dari rekan-rekan yang ingin belajar pemodelan matematika dan optimisasi tapi masih kesulitan dalam memformulasikan masalah real ke dalam bahasa matematika untuk kemudian di-solve dengan berbagai macam optimization solver.

Oleh karena itu saya mencoba menawarkan cara lain dalam menyelesaikan masalah optimisasi seperti masalah konfigurasi pelari estafet sebelumnya.

Pada tulisan tahun lalu, saya memberikan contoh bagaimana simulasi Monte Carlo bisa digunakan sebagai solver masalah optimisasi.

Namun demikian, perlu ditekankan bahwa perlu ada simulasi berulang-ulang kali untuk memastikan solusi yang kita dapatkan adalah solusi yang paling optimal.

---

Penyelesaian dengan Simulasi

Tanpa membuat model matematis yang rumit, kita sebenarnya bisa menyelesaikan masalah di atas dengan cara membuat simulasi urutan pelari yang mungkin. Cara ini sangat sederhana sehingga kita tidak memerlukan library tambahan apapun.

Jika dihitung, berarti ada: = 360 kemungkinan urutan pelari.

TAPI inti dari simulasi bukanlah untuk membuat semua kemungkinan konfigurasi pelari tapi untuk membuat urutan pelari secara random dan mengevaluasi hasinya secara berulang kali.

Berikut adalah flow chart dari algoritmanya:

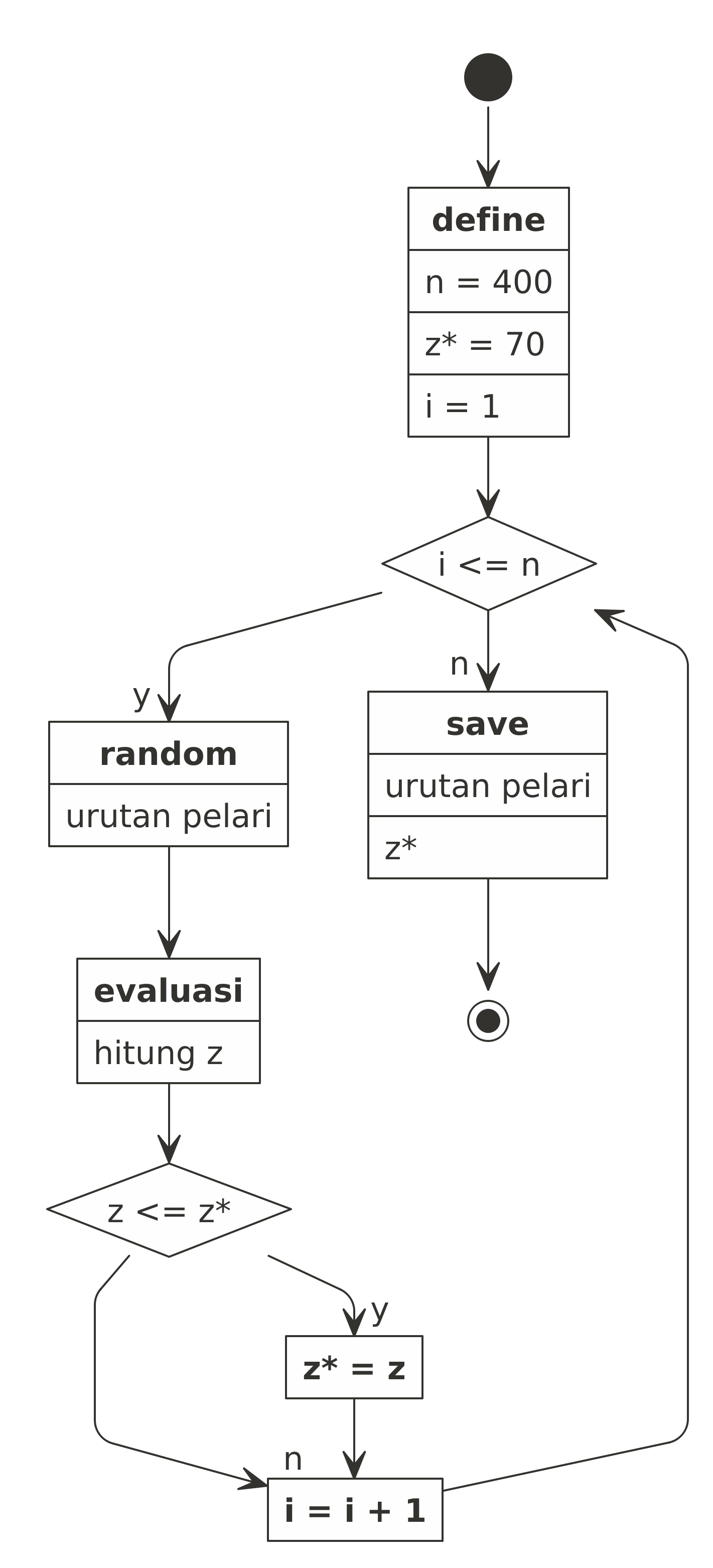
Pada simulasi ini, saya akan buat batas iterasi sebanyak 50 kali. Lalu saya definisikan juga sebagai bentuk reinforce terhadap hasil simulasi. Jika hasil simulasi berhasil mendapatkan nilai yag paling kecil, maka nilai akan di-update nilainya menjadi . Berikut adalah algoritmanya di R:

waktu = rbind(c(12.27,11.57,11.54,12.07),
              c(11.34,11.45,12.45,12.34),
              c(11.29,11.50,11.45,11.52),
              c(12.54,12.34,12.32,11.57),
              c(12.20,11.22,12.07,12.03),
              c(11.54,11.48,11.56,12.30)
)

n = 400
z = 70

for(k in 1:n){
  # simulasi
  runner = sample(1:6,4,replace = F)
  tot_waktu = 0
  for(i in 1:4){
    temp = waktu[runner[i],i]
    tot_waktu = temp + tot_waktu
  }
  
  
  
  # save
  if(tot_waktu < z){
    hasil = list("konfigurasi pelari" = runner,
                 "total waktu (dlm detik)" = tot_waktu)
    z = tot_waktu
  }
  
  data_hasil[k+1,] = list(k,z)
  
}

Berikut adalah hasil yang saya dapatkan:

## $`konfigurasi pelari`
## [1] 2 5 3 4
## 
## $`total waktu (dlm detik)`
## [1] 45.58

---

Jika saya mencoba semua kemungkinan yang ada, saya memerlukan percobaan sebanyak 360 kali.

Bagaimana dengan metode simulasi ini?

Mari kita lihat grafik berikut:

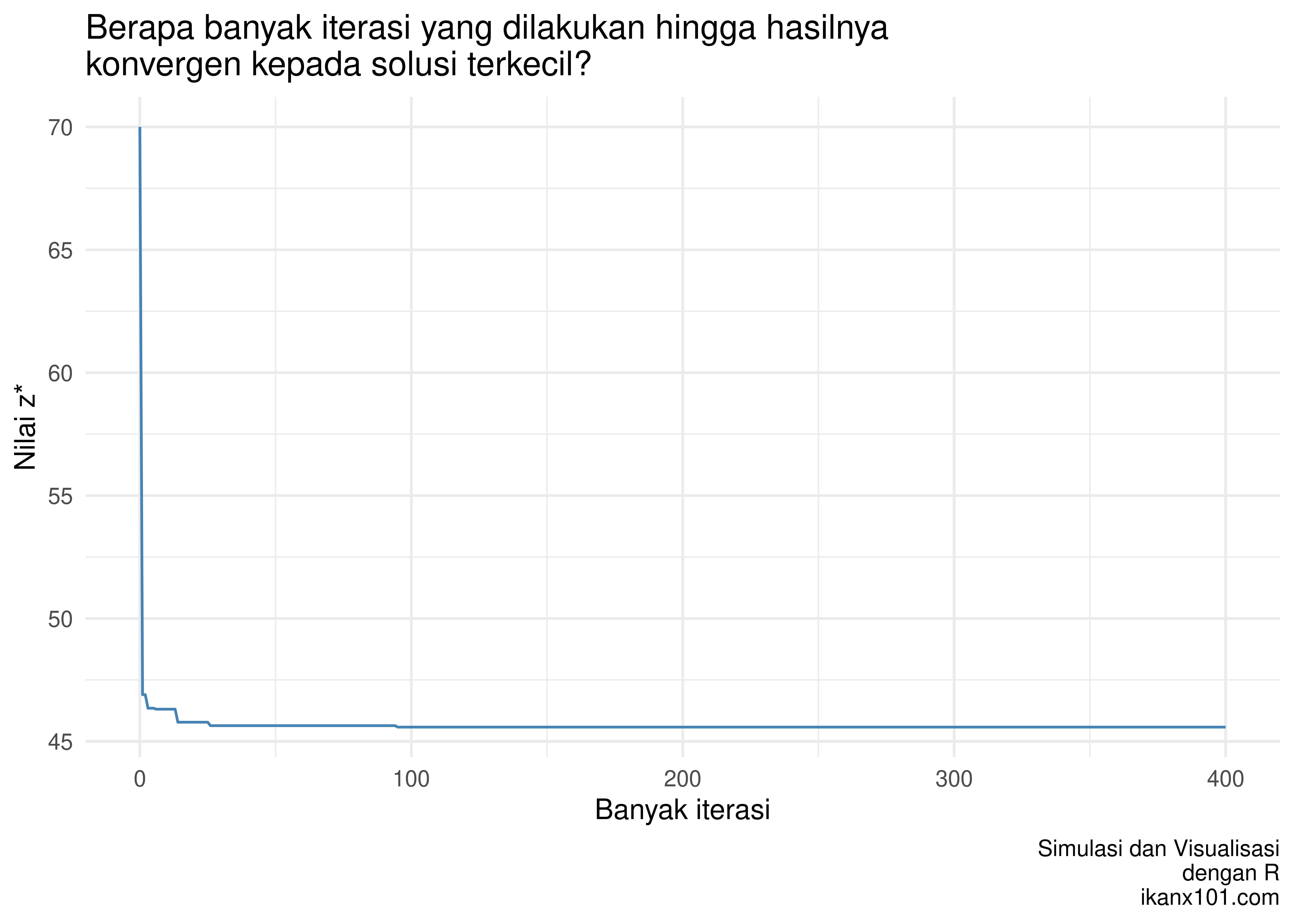
Terlihat bahwa pada iterasi ke 95, hasilnya sudah konvergen.

---

if you find this article helpful, support this blog by clicking the ads.