Marvel Cinematic Universe
Siapa sih yang gak pernah nonton minimal satu film dari Marvel Cinematic Universe?
Dimulai dari film Iron Man pertama dan diakhiri sampai Spiderman Far From Home yang release di tahun ini.
Dari sekian banyak film tersebut, pasti ada sekian film yang menjadi favorit banyak orang. Salah satu parameternya adalah tingginya pendapatan yang diterima oleh film tersebut.
Disadari atau tidak, film yang bagus biasanya dibuat dengan serius juga. Salah satu parameter suatu film digarap dengan serius dapat dilihat dari budget pembuatan film tersebut.
Budget vs Box Office
Dari data yang di- scrap dari the-numbers.com, mari kita lihat hubungan dan apakah mungkin dibuat model antara budget dan box office dari film-film di MCU?
data=read.csv('/cloud/project/Materi Training/GIZ/Latihan SOAL/Marvel Cinematic Universe.csv')
data
## X release_date title production_budget
## 1 1 Jul 2, 2019 Spider-Man: Far From Home 160000000
## 2 2 Apr 26, 2019 Avengers: Endgame 400000000
## 3 3 Mar 8, 2019 Captain Marvel 175000000
## 4 4 Jul 6, 2018 Ant-Man and the Wasp 130000000
## 5 5 Apr 27, 2018 Avengers: Infinity War 300000000
## 6 6 Feb 16, 2018 Black Panther 200000000
## 7 7 Nov 3, 2017 Thor: Ragnarok 180000000
## 8 8 Jul 7, 2017 Spider-Man: Homecoming 175000000
## 9 9 May 5, 2017 Guardians of the Galaxy Vol 2 200000000
## 10 10 Nov 4, 2016 Doctor Strange 165000000
## 11 11 May 6, 2016 Captain America: Civil War 250000000
## 12 12 Jul 17, 2015 Ant-Man 130000000
## 13 13 May 1, 2015 Avengers: Age of Ultron 330600000
## 14 14 Aug 1, 2014 Guardians of the Galaxy 170000000
## 15 15 Apr 4, 2014 Captain America: The Winter… 170000000
## 16 16 Nov 8, 2013 Thor: The Dark World 150000000
## 17 17 May 3, 2013 Iron Man 3 200000000
## 18 18 May 4, 2012 The Avengers 225000000
## 19 19 Jul 22, 2011 Captain America: The First … 140000000
## 20 20 May 6, 2011 Thor 150000000
## 21 21 May 7, 2010 Iron Man 2 170000000
## 22 22 Jun 13, 2008 The Incredible Hulk 137500000
## 23 23 May 2, 2008 Iron Man 186000000
## worldwide_box_office
## 1 1131723455
## 2 2797800564
## 3 1126129839
## 4 623144660
## 5 2048359754
## 6 1348258224
## 7 853958289
## 8 880166350
## 9 869113101
## 10 676404566
## 11 1153284349
## 12 518858449
## 13 1403013963
## 14 772772112
## 15 714401889
## 16 644602516
## 17 1215392272
## 18 1517935897
## 19 370569776
## 20 449326618
## 21 621156389
## 22 265573859
## 23 585171547
str(data)
## 'data.frame': 23 obs. of 5 variables:
## $ X : int 1 2 3 4 5 6 7 8 9 10 ...
## $ release_date : Factor w/ 23 levels "Apr 26, 2019",..: 7 1 12 9 2 5 21 10 17 22 ...
## $ title : Factor w/ 23 levels "Ant-Man","Ant-Man and the Wasp",..: 17 4 10 2 5 6 22 18 13 11 ...
## $ production_budget : int 160000000 400000000 175000000 130000000 300000000 200000000 180000000 175000000 200000000 165000000 ...
## $ worldwide_box_office: num 1.13e+09 2.80e+09 1.13e+09 6.23e+08 2.05e+09 ...
Kalau kita lihat, dari dataset terdapat variabel-variabel berikut ini:
X: nomor urutrelease_date: tanggal release filmtitle: judul film MCUproduction_budget: budget produksi filmworldwide_box_office: pendapatan film worldwide
Nah, sebenarnya tidak semua data ini kita butuhkan yah. Minimal kita hanya butuh judul film dan dua variabel yang akan kita buat modelnya.
So, mari kita bebersih dulu.
library(dplyr)
data =
data %>% mutate(X=NULL,release_date=NULL)
colnames(data) = c('judul','budget','box_office')
head(data)
## judul budget box_office
## 1 Spider-Man: Far From Home 160000000 1131723455
## 2 Avengers: Endgame 400000000 2797800564
## 3 Captain Marvel 175000000 1126129839
## 4 Ant-Man and the Wasp 130000000 623144660
## 5 Avengers: Infinity War 300000000 2048359754
## 6 Black Panther 200000000 1348258224
summary(data)
## judul budget box_office
## Ant-Man : 1 Min. :130000000 Min. :2.656e+08
## Ant-Man and the Wasp : 1 1st Qu.:155000000 1st Qu.:6.222e+08
## Avengers: Age of Ultron: 1 Median :175000000 Median :8.540e+08
## Avengers: Endgame : 1 Mean :195395652 Mean :9.820e+08
## Avengers: Infinity War : 1 3rd Qu.:200000000 3rd Qu.:1.184e+09
## Black Panther : 1 Max. :400000000 Max. :2.798e+09
## (Other) :17
Statistika deskripsi
Sebelum mulai bagian serunya, kita akan liat statistika deskripsi dari
variabel budget dan box_office yuk.
Budget
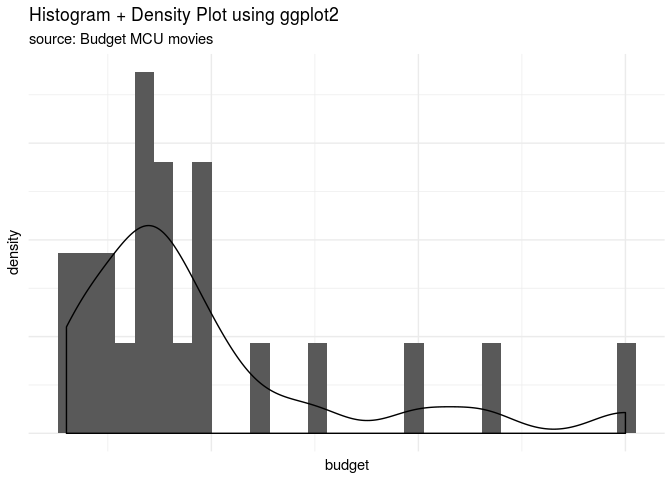
Mari kita lihat sebaran dari variabel budget.
library(ggplot2)
#histogram dengan ggplot2
data %>%
ggplot(aes(x=budget)) +
geom_histogram(aes(y=..density..)) +
geom_density() +
labs(title='Histogram + Density Plot using ggplot2',
subtitle='source: Budget MCU movies') +
theme_minimal() +
theme(axis.text = element_blank())
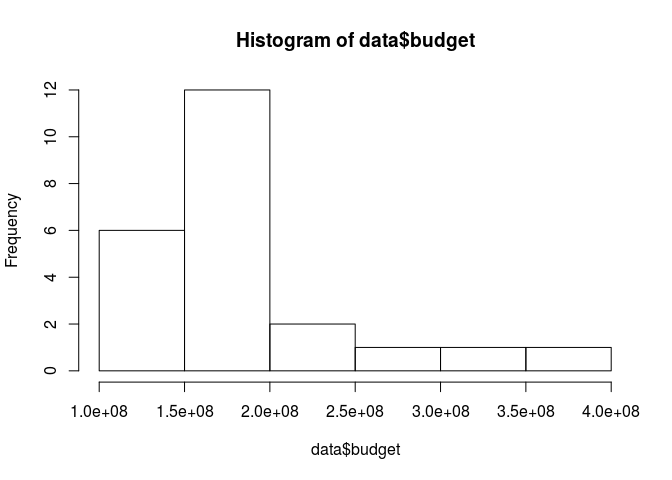
#histogram dengan base
hist(data$budget)
#boxplot dengan base
data %>% ggplot(aes(y=budget)) + geom_boxplot()
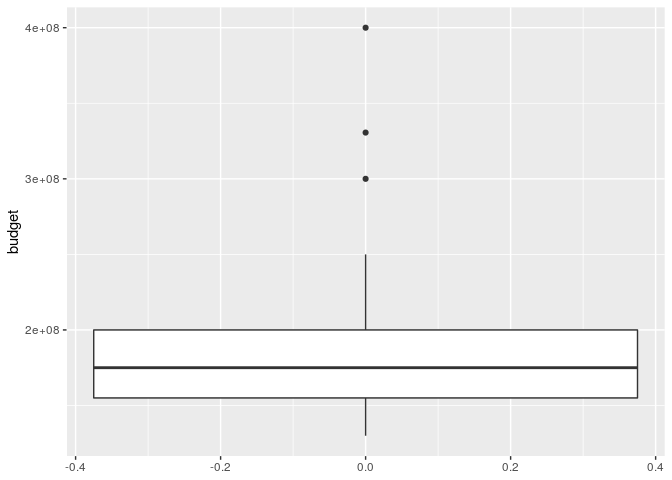
Dari sebaran datanya, terlihat bahwa budget agak miring ke kiri. Ada
tiga film yang memiliki budget sangat tinggi yang berada di luar
jangkauan boxplot-nya.
Apakah budget berdistribusi normal? Kita lakukan uji shapiro-wilk
stat_uji = shapiro.test(data$budget)
ifelse(stat_uji$p.value < 0.05,
'Tolak H0 -- tidak normal',
'H0 tidak ditolak -- normal')
## [1] "Tolak H0 -- tidak normal"
Ternyata didapatkan bahwa variabel budget tidak berdistribusi
normal.
Box Office
Sekarang giliran kita lihat sebaran dari variabel Box Office.
library(ggplot2)
#histogram dengan ggplot2
data %>%
ggplot(aes(x=box_office)) +
geom_histogram(aes(y=..density..)) +
geom_density() +
labs(title='Histogram + Density Plot using ggplot2',
subtitle='source: Box Office MCU movies') +
theme_minimal() +
theme(axis.text = element_blank())
#histogram dengan base
hist(data$box_office)
#boxplot dengan base
data %>% ggplot(aes(y=box_office)) + geom_boxplot()
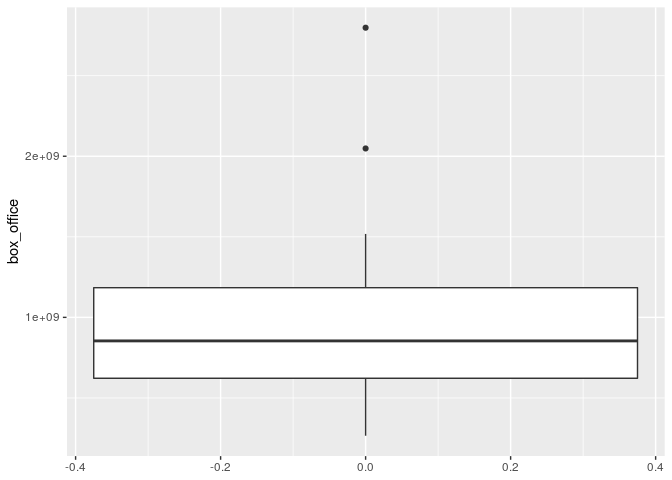
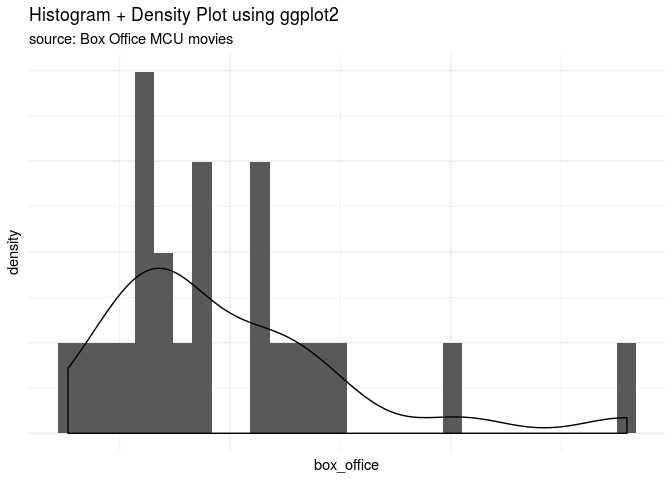
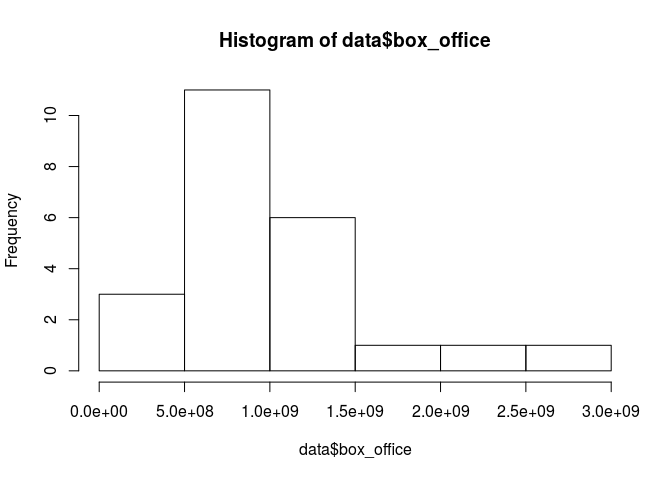
Dari sebaran datanya, terlihat bahwa box_office agak miring ke kiri.
Ada dua film yang memiliki box_office sangat tinggi yang berada di
luar jangkauan boxplot-nya. Menarique, ternyata ada dua yang
tinggi sedangkan tadi pas budget ada tiga film.
Apakah box_office berdistribusi normal? Kita lakukan uji
shapiro-wilk
stat_uji = shapiro.test(data$box_office)
ifelse(stat_uji$p.value < 0.05,
'Tolak H0 -- tidak normal',
'H0 tidak ditolak -- normal')
## [1] "Tolak H0 -- tidak normal"
Ternyata didapatkan bahwa variabel box_office tidak berdistribusi
normal.
Korelasi Antara Budget dan Box Office
Sekarang, kita akan hitung korelasi antara keduanya yah. Karena kita tahu bahwa kedua variabel tersebut tidak berdistribusi normal, maka kita akan gunakan korelasi spearman.
korel = cor(data$budget,data$box_office,method = 'spearman')
korel
## [1] 0.8476623
Ternyata didapatkan angka korelasi yang kuat dan positif. Yakni sebesar
0.8476623. Apa sih artinya?
Model Kausalitas Budget dan Box Office
Perlu diingat bahwa korelasi hanya menghitung hubungan linear antara dua
variabel saja. Jika kita ingin mencari tahu apakah budget menyebabkan
box_office, dinotasikan: (box_office~budget), maka perlu dibuat
modelnya.
Model paling mudah untuk tipe data numerik - numerik adalah model regresi linear.
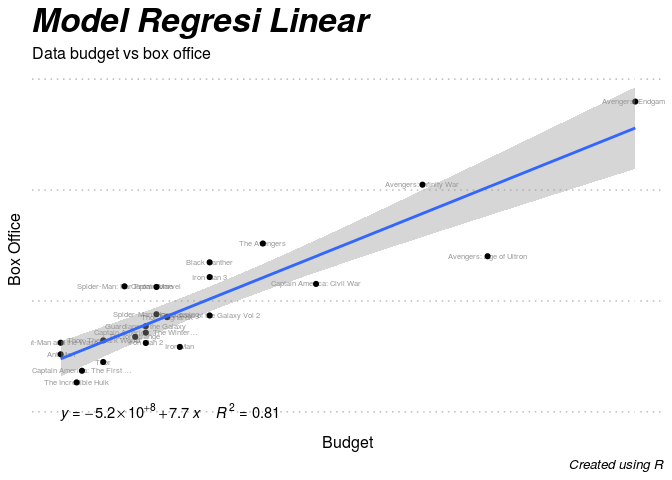
y = a*x + b + error biasa ditulis dengan simpel sebagai: y = a*x +
b.
Oh iya, apakah model regresi linear mengharusnya variabel X dan Y berdistribusi normal? Kindly komen yah…
Yuk kita buat model regresi linearnya!
#membuat modelnya
model_reg = lm(box_office~budget,data = data)
# memanggil modelnya
model_reg
##
## Call:
## lm(formula = box_office ~ budget, data = data)
##
## Coefficients:
## (Intercept) budget
## -5.245e+08 7.710e+00
# melihat keseluruhan model
summary(model_reg)
##
## Call:
## lm(formula = box_office ~ budget, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -621459620 -173906794 -9389925 218048707 422575157
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -5.245e+08 1.699e+08 -3.087 0.00558 **
## budget 7.710e+00 8.240e-01 9.357 6.12e-09 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 259700000 on 21 degrees of freedom
## Multiple R-squared: 0.8065, Adjusted R-squared: 0.7973
## F-statistic: 87.55 on 1 and 21 DF, p-value: 6.122e-09
Model fitness
Ada beberapa parameter yang bisa digunakan untuk melihat apakah model kita fit atau tidak, yakni:
- R squared
- P-value
- MAE ( mean absolut error )
- Lainnya
R squared
Nilainya bisa diambil dari nilai multiple R-squared pada model atau bisa juga dihitung menggunakan:
r_squared = modelr::rsquare(model_reg,data)
r_squared
## [1] 0.8065491
Perlu diperhatikan, bahwa nilai R squared bisa dihitung juga dari nilai korelasi yang dikuadratkan. Namun ternyata untuk kali ini tidak bisa dilakukan.
r_squared == korel^2
## [1] FALSE
Ada yang tahu kenapa?
Jawabnya karena korelasi yang digunakan adalah spearman. Jika digunakan dengan pearson maka pasti nilainya sama.
Oh iya, ada yang tahu gak apa arti dari R-squared? R-squared bisa diartikan sebagai:
Berapa persen variabel X meng- explain variabel Y.
P-value
Nilai P-value didapatkan dari summary(model_reg), yakni mendekati nol
(sangat kecil). Oleh karena p-value < 0.05 bisa diambil kesimpulan
bahwa model berpengaruh terhadap box_office.
MAE
Mean absolut error dapat diartikan sebagai rata-rata nilai mutlak error yang dapat kita terima. Tidak ada angka pasti harus berapa, tapi semakin kecil error, berarti semakin baik model kita.
mean_absolut_error = modelr::mae(model_reg,data)
mean_absolut_error
## [1] 201077629
Kesimpulan
Berhubung dari p-value dan R squared menghasilkan nilai yang baik, dapat
disimpulkan bahwa budget film MCU mempengaruhi dan mengakibatkan
box_office secara positif dan kuat.
Cara lain
Sebenarnya ada cara lain untuk melakukan analisa regresi linear
menggunakan R, yakni dengan memanfaatkan library ggplot2 dan
ggpubr.
library(ggplot2)
library(ggpubr)
data %>% ggplot(aes(x=budget,y=box_office)) +
geom_point() +
geom_text(aes(label=judul),alpha=.4,size=2) +
geom_smooth(method='lm') +
theme_pubclean() +
stat_regline_equation(label.y = 7,aes(label = paste(..eq.label.., ..rr.label.., sep = "~~~~"))) +
labs(title = 'Model Regresi Linear',
subtitle = 'Data budget vs box office',
caption = 'Created using R',
x = 'Budget',
y = 'Box Office') +
theme(axis.text = element_blank(),
axis.ticks = element_blank(),
plot.title = element_text(size=25,face='bold.italic'),
plot.caption = element_text(size=10,face='italic'))