Kegunaan Monte Carlo Lagi (Daily Use)

Ternyata saya sudah puasa ngeblog beberapa minggu ini. Padahal draft tulisan yang saya buat ada lumayan banyak. Tapi entah kenapa saya seperti belum menemukan momen yang pas to publish those drafts.

Kalau mau lihat, bisa cek github saya dan lihat masing-masing markdown yang tercipta selama 2 minggu belakangan.

Nah, kali ini saya hendak membahas simulasi Monte Carlo (lagi) untuk menghitung dan menyelesaikan masalah yang receh.

Seberapa receh?

Receh banget lah.

---

Masalah 1: Absensi Karyawan

Suatu ketika, seorang manager suatu bagian tertentu di kantor mendapatkan email laporan dari bagian HR terkait absensi seorang anak buahnya yang agak bermasalah. Kira-kira, begini highlight emailnya:

Anak buah Anda bernama XYZ memiliki catatan keterlambatan yang tinggi. Ia biasa terlambat datang ke kantor rata-rata dua dari lima hari kerja.

Sayangnya tidak ada keterangan data historikal pada hari apa saja si XYZ biasa terlambat.

Berdasarkan informasi yang ada, si manager ingin menghitung berapa peluang si XYZ terlambat di hari Senin DAN Jumat dalam seminggu.

Bagaimana caranya?

Yuk kita selesaikan!

Saya akan membuat beberapa baris algoritma untuk membuat simulasi ini yah. Mungkin bukan algoritma yang tidy, tapi saya akan buat yang sangat simpel sehingga mudah dimengerti.

Pertama, kita buat dulu fungsi apakah karyawan tersebut datang telat atau tidak dalam suatu hari?

telat = function(){
  sample(c(T,F),1,prob = c(2/5,3/5))
}
telat()

## [1] TRUE

Kedua, berbekal fungsi di atas, kita buat fungsi untuk menghitung berapa kali dia akan datang telat dalam 5 hari kerja.

telat_seminggu = function(){
  sample(c(T,F),5,replace = T,prob = c(2/5,3/5))
}
minggu_ini = telat_seminggu()
minggu_ini # keterlambatan yang terjadi dalam seminggu ini

## [1] FALSE FALSE FALSE FALSE FALSE

sum(minggu_ini) # berapa kali telat dalam 5 hari kerja?

## [1] 0

Ketiga, berbekal fungsi di atas, kita buat fungsi yang mengecek apakah karyawan tersebut terlambat di Senin dan Jumat.

senin_jumat_telat = function(){
  minggu = telat_seminggu()
  senin = minggu[1]
  jumat = minggu[5]
  dummy = sum(senin+jumat)
  ifelse(dummy == 2, 1, 0) # jika terjadi keterlambatan di Senin dan Jumat, akan diberi skor = 1
}
senin_jumat_telat()

## [1] 0

Keempat, kita akan buat fungsi untuk melakukan simulasi berkali-kali lalu kita hitung peluangnya.

simulasi = function(n){
  hasil = 0
  for(i in 1:n){
    dummy = senin_jumat_telat()
    hasil = hasil + dummy
  }
  return(hasil/n)
}

Kelima, sekarang kita lakukan simulasinya yah.

data = data.frame(langkah=c(1:2000))
data$peluang_simulasi = sapply(data$langkah,simulasi)

# hasil 10 simulasi pertama
head(data,10)

##    langkah peluang_simulasi
## 1        1             1.00
## 2        2             0.00
## 3        3             0.00
## 4        4             0.25
## 5        5             0.00
## 6        6             0.00
## 7        7             0.00
## 8        8             0.50
## 9        9             0.00
## 10      10             0.20

# hasil 10 simulasi terakhir
tail(data,10)

##      langkah peluang_simulasi
## 1991    1991        0.1612255
## 1992    1992        0.1661647
## 1993    1993        0.1650778
## 1994    1994        0.1489468
## 1995    1995        0.1563910
## 1996    1996        0.1437876
## 1997    1997        0.1507261
## 1998    1998        0.1496496
## 1999    1999        0.1450725
## 2000    2000        0.1675000

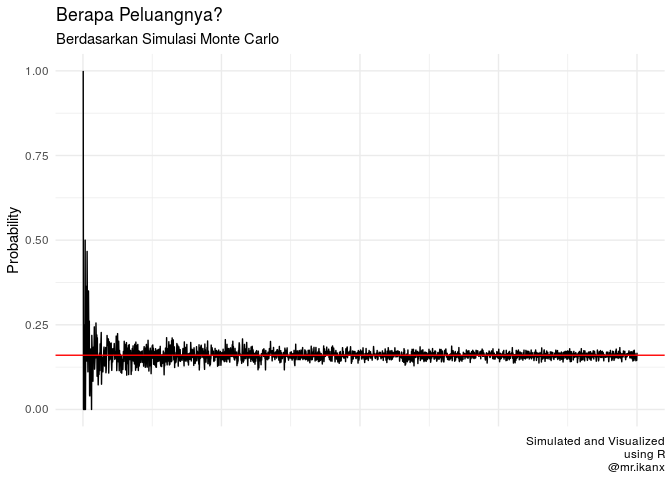
Jadi berapa peluang si karyawan itu datang telat di Senin DAN Jumat?

mean(data$peluang_simulasi)

## [1] 0.1601322

---

Masalah 2: Mencari Responden Horang Kayah

Suatu ketika saya diminta untuk melaksanakan survey di suatu kota. Salah satu kriteria responden yang dicari adalah memiliki sosial ekonomi status yang tinggi alias horang kayah.

Berdasarkan data yang saya punya dari AC Nielsen, proporsi horang kayah di kota tersebut ada sebesar 13% dari populasi kota tersebut.

Pertanyaannya:

Jika pemilihan responden dilakukan secara random, berapa banyak orang responden yang harus saya temui sampai saya bisa mendapatkan 30 orang responden horang kayah tersebut?

Bagaimana cara menjawabnya?

Gak usah pake simulasi, ribet banget sih!

Oke, sekarang kita akan menghitungnya tanpa menggunakan simulasi. Bagaimana caranya?

Tinggal dibagi saja 30 dengan 13% yah!

n = 30 / (13/100)
n

## [1] 230.7692

Setidaknya saya membutuh sekitar 230 orang responden agar saya bisa mendapatkan 30 orang responden horang kayah.

Sekarang kita selesaikan dengan simulasi:

Kenapa sih harus diselesaikan dengan simulasi?

Kadang simulasi dibutuhkan karena kita ingin mendapatkan jawaban berupa selang atau rentang karena kita berhadapan dengan masalah peluang di sini. Sedangkan jawaban 230.7 adalah jawaban eksak.

Nanti hasil expected value dari simulasi seharusnya mirip dengan jawaban eksak.

Mari kita buat simulasinya yah.

Fungsi pertama adalah melihat apakah kita mendapatkan responden yang tepat.

tepat = function(){
  sample(c(1,0),1,prob = c(13/100,87/100))
}
tepat()

## [1] 0

Fungsi kedua adalah untuk melakukan looping dengan while() agar didapatkan sampel 30 horang kayah.

cari_n = function(){
  n = 0
  i = 0
    while(n<30){
      dummy = tepat()
      n = n+dummy
      i = i+1
    }
return(i)
}

Sekarang, kita akan lakukan simulasinya berulang kali sehingga didapatkan hasil sebagai berikut:

data = data.frame(id=c(1:2500))
data$banyak_resp = 0

for(i in 1:length(data$id)){
  data$banyak_resp[i] = cari_n()
}

Mari kita hitung expected value dari simulasi ini, yakni sebesar:

mean(data$banyak_resp)

## [1] 230.526

Kalau dibandingkan, hasil expected value dari simulasi dan perhitungan eksak memiliki hasil yang hampir sama.

Nah, sekarang apa kelebihan simulasi? Kita bisa lihat selang perkiraannya sebagai berikut:

data %>% ggplot(aes(y = banyak_resp)) + geom_boxplot(notch=TRUE) +
  theme_minimal() +
  labs(subtitle = 'Boxplot Hasil Simulasi Monte Carlo',
       title = 'Berapa banyak responden yang harus saya wawancara agar mendapatkan\nhorang kayah sebanyak 30 orang?',
       caption = 'Simulated and Visualized\nusing R\n@mr.ikanx',
       y = 'Banyak orang') +
  theme(axis.title.x = element_blank(),
        axis.text.x = element_blank())

Karena saya melakukan simulasi ini sekian ribu kali, maka dengan memanfaatkan Central Limit Theorem, saya mengasumsikan data ini berdistribusi normal.

Masih ingat hubungan histogram dan boxplot dari distribusi normal berikut ini?

Sehingga saya bisa menyimpulkan bahwa daerah antara Q1 dan Q3 adalah selang perkiraan saya inginkan karena mengcover 50% dari data yang mungkin muncul.

summary(data$banyak_resp)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   121.0   203.0   229.0   230.5   256.0   367.0

Jadi untuk mendapatkan horang kayah sebanyak 30 orang, saya perlu mewawancarai sekitar 203 - 256 orang.