Membuat Regresi Non Linear dengan Cara Transformasi Data

Seringkali kita mendapatkan dua data yang saling berhubungan sebab akibat tapi tidak dalam hubungan linear. Jika kita ingin membuat model regresi non linear yang “akurat” dengan mengandalkan regresi linear, kita bisa lakukan transformasi data.

Misalkan saya punya contoh tabel data sebagai berikut:

V1	V2
2.5134000	0.00
2.0443334	0.05
1.6684044	0.10
1.3664180	0.15
1.1232325	0.20
0.9268897	0.25
0.7679339	0.30
0.6388776	0.35
0.5337835	0.40
0.4479364	0.45
0.3775848	0.50
0.3197393	0.55
0.2720131	0.60
0.2324966	0.65
0.1996590	0.70
0.1722704	0.75
0.1493406	0.80
0.1300700	0.85
0.1138119	0.90
0.1000416	0.95
0.0883321	1.00
0.0783354	1.05
0.0697669	1.10
0.0623931	1.15

Jika kita perhatikan dengan seksama, data pada kolom V2 memiliki penambahan yang linear dan konstan sedangkan data pada kolom V1 cenderung menurun tak linear. Saya akan coba gambarkan dalam scatterplot sebagai berikut:

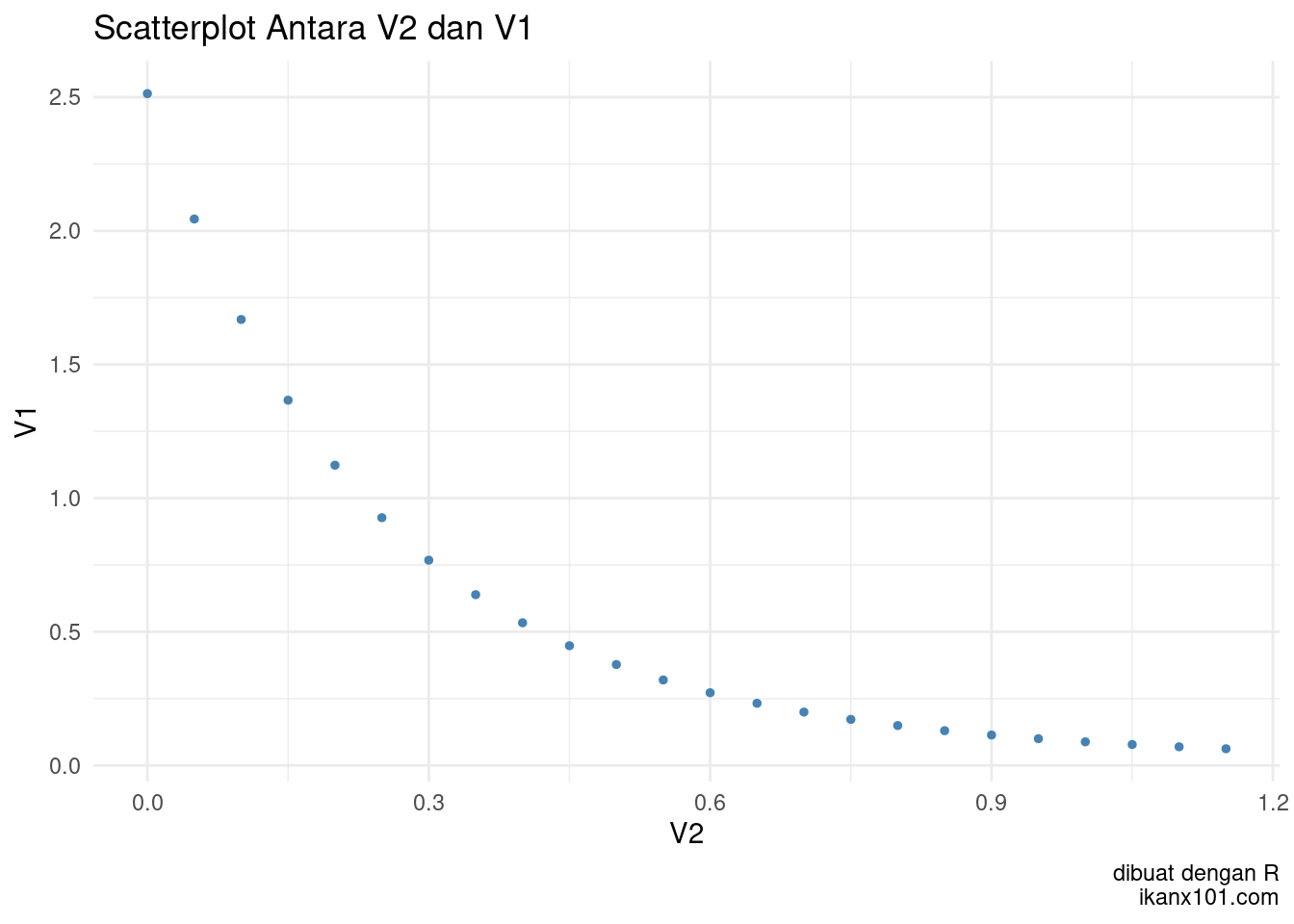
Terlihat hubungan V1 dan V2 tidak linear. Oleh karena itu, saya akan mencoba melakukan transformasi data di sumbu (yaitu kolom V1). Untuk itu, fungsi transformasi yang saya pilih adalah:

# transformasi nilai y menjadi y_hat
df = df %>% mutate(V1_hat = log(V1))
# print data ke laporan
df %>% knitr::kable(caption = "Data Hasil Transformasi")

V1	V2	V1_hat
2.5134000	0.00	0.9216364
2.0443334	0.05	0.7150718
1.6684044	0.10	0.5118677
1.3664180	0.15	0.3121927
1.1232325	0.20	0.1162107
0.9268897	0.25	-0.0759207
0.7679339	0.30	-0.2640517
0.6388776	0.35	-0.4480425
0.5337835	0.40	-0.6277649
0.4479364	0.45	-0.8031041
0.3775848	0.50	-0.9739601
0.3197393	0.55	-1.1402492
0.2720131	0.60	-1.3019051
0.2324966	0.65	-1.4588799
0.1996590	0.70	-1.6111446
0.1722704	0.75	-1.7586899
0.1493406	0.80	-1.9015259
0.1300700	0.85	-2.0396824
0.1138119	0.90	-2.1732079
0.1000416	0.95	-2.3021696
0.0883321	1.00	-2.4266518
0.0783354	1.05	-2.5467552
0.0697669	1.10	-2.6625951
0.0623931	1.15	-2.7743002

Data Hasil Transformasi

Saya akan buat scatterplot kembali dari data yang ada:

Kita bisa lihat sekilas bahwa V1_hat relatif lebih linear dibandingkan V1 asalnya. Selanjutnya saya akan membuat fungsi regresi linear antara V2 dan V1_hat sebagai berikut:

# membuat model regresi linear
reg_lin = lm(V1_hat~V2,data = df)
summary(reg_lin)

## 
## Call:
## lm(formula = V1_hat ~ V2, data = df)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.10833 -0.08469 -0.02505  0.06628  0.19046 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.73863    0.03959   18.66 5.67e-15 ***
## V2          -3.22034    0.05899  -54.59  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.1 on 22 degrees of freedom
## Multiple R-squared:  0.9927, Adjusted R-squared:  0.9923 
## F-statistic:  2980 on 1 and 22 DF,  p-value: < 2.2e-16

Kita dapatkan formula regresi linear sebagai berikut:

dengan adjusted (berarti model memiliki performa yang sangat baik). Saya akan coba buat tabel dan grafiknya kembali sebagai berikut:

# fungsi regresi linear
reg_lin = function(x){0.73863 - 3.22034 * x}

# menghitung aproksimasi V1_reg dari V2 berdasarkan model regresi linear
df = 
  df %>% 
  rowwise() %>% 
  mutate(V1_reg = reg_lin(V2)) %>% 
  ungroup()

V1	V2	V1_hat	V1_reg
2.5134000	0.00	0.9216364	0.738630
2.0443334	0.05	0.7150718	0.577613
1.6684044	0.10	0.5118677	0.416596
1.3664180	0.15	0.3121927	0.255579
1.1232325	0.20	0.1162107	0.094562
0.9268897	0.25	-0.0759207	-0.066455
0.7679339	0.30	-0.2640517	-0.227472
0.6388776	0.35	-0.4480425	-0.388489
0.5337835	0.40	-0.6277649	-0.549506
0.4479364	0.45	-0.8031041	-0.710523
0.3775848	0.50	-0.9739601	-0.871540
0.3197393	0.55	-1.1402492	-1.032557
0.2720131	0.60	-1.3019051	-1.193574
0.2324966	0.65	-1.4588799	-1.354591
0.1996590	0.70	-1.6111446	-1.515608
0.1722704	0.75	-1.7586899	-1.676625
0.1493406	0.80	-1.9015259	-1.837642
0.1300700	0.85	-2.0396824	-1.998659
0.1138119	0.90	-2.1732079	-2.159676
0.1000416	0.95	-2.3021696	-2.320693
0.0883321	1.00	-2.4266518	-2.481710
0.0783354	1.05	-2.5467552	-2.642727
0.0697669	1.10	-2.6625951	-2.803744
0.0623931	1.15	-2.7743002	-2.964761

Sekarang dari kolom V1_reg, akan saya kembalikan ke bentuk asalnya dengan fungsi inverse dari transformasi yang telah dilakukan sebelumnya:

# menginverse transformasi yang dilakukan
df = 
  df %>% 
  mutate(V1_inv = exp(V1_reg))

V1	V2	V1_hat	V1_reg	V1_inv
2.5134000	0.00	0.9216364	0.738630	2.0930660
2.0443334	0.05	0.7150718	0.577613	1.7817802
1.6684044	0.10	0.5118677	0.416596	1.5167896
1.3664180	0.15	0.3121927	0.255579	1.2912090
1.1232325	0.20	0.1162107	0.094562	1.0991773
0.9268897	0.25	-0.0759207	-0.066455	0.9357050
0.7679339	0.30	-0.2640517	-0.227472	0.7965447
0.6388776	0.35	-0.4480425	-0.388489	0.6780807
0.5337835	0.40	-0.6277649	-0.549506	0.5772349
0.4479364	0.45	-0.8031041	-0.710523	0.4913871
0.3775848	0.50	-0.9739601	-0.871540	0.4183069
0.3197393	0.55	-1.1402492	-1.032557	0.3560953
0.2720131	0.60	-1.3019051	-1.193574	0.3031359
0.2324966	0.65	-1.4588799	-1.354591	0.2580528
0.1996590	0.70	-1.6111446	-1.515608	0.2196746
0.1722704	0.75	-1.7586899	-1.676625	0.1870041
0.1493406	0.80	-1.9015259	-1.837642	0.1591924
0.1300700	0.85	-2.0396824	-1.998659	0.1355169
0.1138119	0.90	-2.1732079	-2.159676	0.1153625
0.1000416	0.95	-2.3021696	-2.320693	0.0982055
0.0883321	1.00	-2.4266518	-2.481710	0.0836001
0.0783354	1.05	-2.5467552	-2.642727	0.0711669
0.0697669	1.10	-2.6625951	-2.803744	0.0605828
0.0623931	1.15	-2.7743002	-2.964761	0.0515728

Bentuk persamaan regresi finalnya adalah:

---

if you find this article helpful, support this blog by clicking the ads