Teknik Resampling dengan Metode Monte Carlo

Beberapa hari ini, saya diminta melakukan resampling dari suatu large dataset agar proporsi strata yang ada menjadi sesuai dengan keinginan. Metode pertama yang langsung terlintas dalam pikiran saya adalah menggunakan metode simulasi Monte Carlo.

Bingung yah maksudnya apa?

Oke, saya coba jelaskan dengan analogi sederhana berikut:

Analogi

Di suatu toko buah, ada 4 jenis buah yang dijual yaitu: apel, jeruk, mangga, dan salak. Dari informasi supplier, diketahui:

1. Sebanyak 35 buah dari total 100 buah apel berasa masam (belum matang).
2. Sebanyak 25 buah dari total 55 buah jeruk berasa masam.
3. Sebanyak 40 buah dari total 60 buah mangga berasa masam.
4. Sebanyak 15 buah dari total 75 buah salak berasa masam.

Setiap jenis buah ditempatkan di baknya masing-masing (terpisah) dan tidak bisa dibedakan secara kasat mata mana yang masam dan manis.

Lalu seorang pelanggan datang dan mengambil:

• 4 buah apel,
• 8 buah jeruk,
• 3 buah mangga,
• 5 buah salak.

Berapa banyak buah masam yang bisa diperoleh pelanggan tersebut?

---

Jika kita pikirkan kembali, ada tiga kemungkinan yang bisa terjadi. Yakni:

1. Si pelanggan mengambil semua buah masam (20 buah masam).
2. Si pelanggan tidak mengambil buah yang masam sama sekali (0 buah masam).
3. Si pelanggan mengambil 1 ≤ n ≤ 19 buah yang masam.

Jadi masalah saya sekarang adalah menghitung kira-kira berapa buah masam yang berpeluang tinggi bisa diterima pelanggan (expected value).

Prinsip dari simulasi adalah dengan membuat seolah-olah ada banyak pelanggan datang, mengambil buah, lalu menghitung berapa banyak yang masam. Semua pelanggan akan direkap, rata-rata berapa banyak buah masam akan dihitung. Kira-kira begini ilustrasinya:

Simulasi akan mengulang-ulang proses di atas hingga ribuan bahkan jutaan kali.

Kenapa harus sebegitu banyaknya pengulangan?

Pernah mendengar istilah law of large number? Semakin banyak kejadian pelanngan mengambil buah, kita bisa melihat sebenarnya seberapa banyak buah masam yang bisa diambil oleh pelanggan.

Saya membuat algoritma yang melakukan 50.000 pengulangan sebagai berikut:

# probability
p_apel = 35/100
p_jeruk = 25/55
p_mangga = 40/60
p_salak = 15/75

# yang diambil pelanggan
n_apel = 4
n_jeruk = 8
n_mangga = 3
n_salak = 5

# simulasi
busuk = c()
n_simu = 50000
# iterasi
for(i in 1:n_simu){
  apel = sample(c(1,0),n_apel,replace = T,prob = c(p_apel,1-p_apel))
  jeruk = sample(c(1,0),n_jeruk,replace = T,prob = c(p_jeruk,1-p_jeruk))
  mangga = sample(c(1,0),n_mangga,replace = T,prob = c(p_mangga,1-p_mangga))
  salak = sample(c(1,0),n_salak,replace = T,prob = c(p_salak,1-p_salak))
  buah_busuk = sum(apel,jeruk,mangga,salak)
  busuk = c(buah_busuk,busuk)
}
# rekap hasl simulasi
rekap_simulasi = data.frame(iter = 1:n_simu,busuk)

Hasilnya didapatkan sebaran buah masam yang bisa diambil pelanggan sebagai berikut:

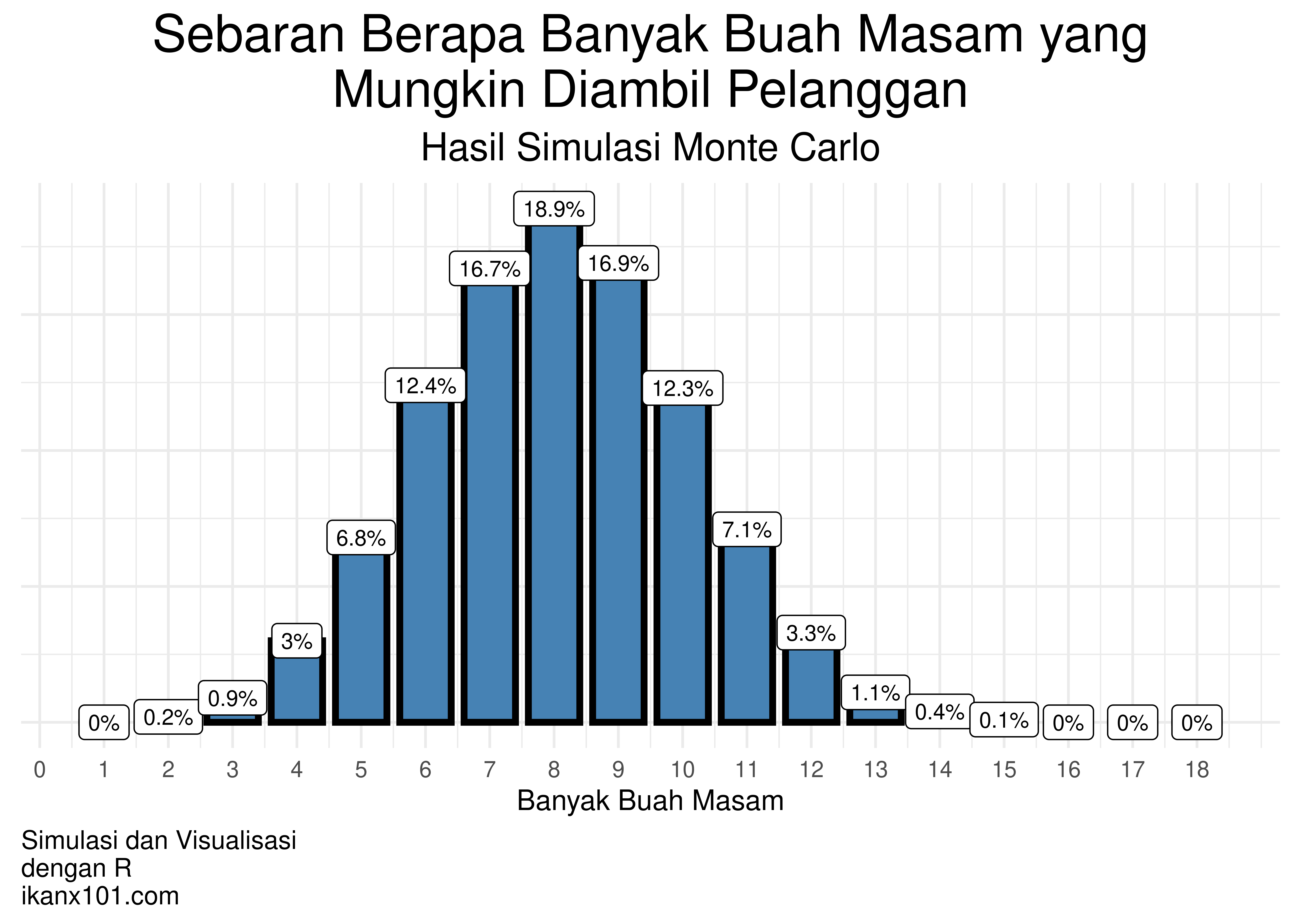
dari grafik sebaran di atas, terlihat bahwa expected value buah masam yang diambil pelanggan adalah sekitar 8 buah. Jika saya ambil selang kepercayaan sebesar 91%, pelanggan bisa mendapatkan buah masam sekitar 5-11 buah.

Sekarang kita lihat nilai expected value buah masam dari simulasinya:

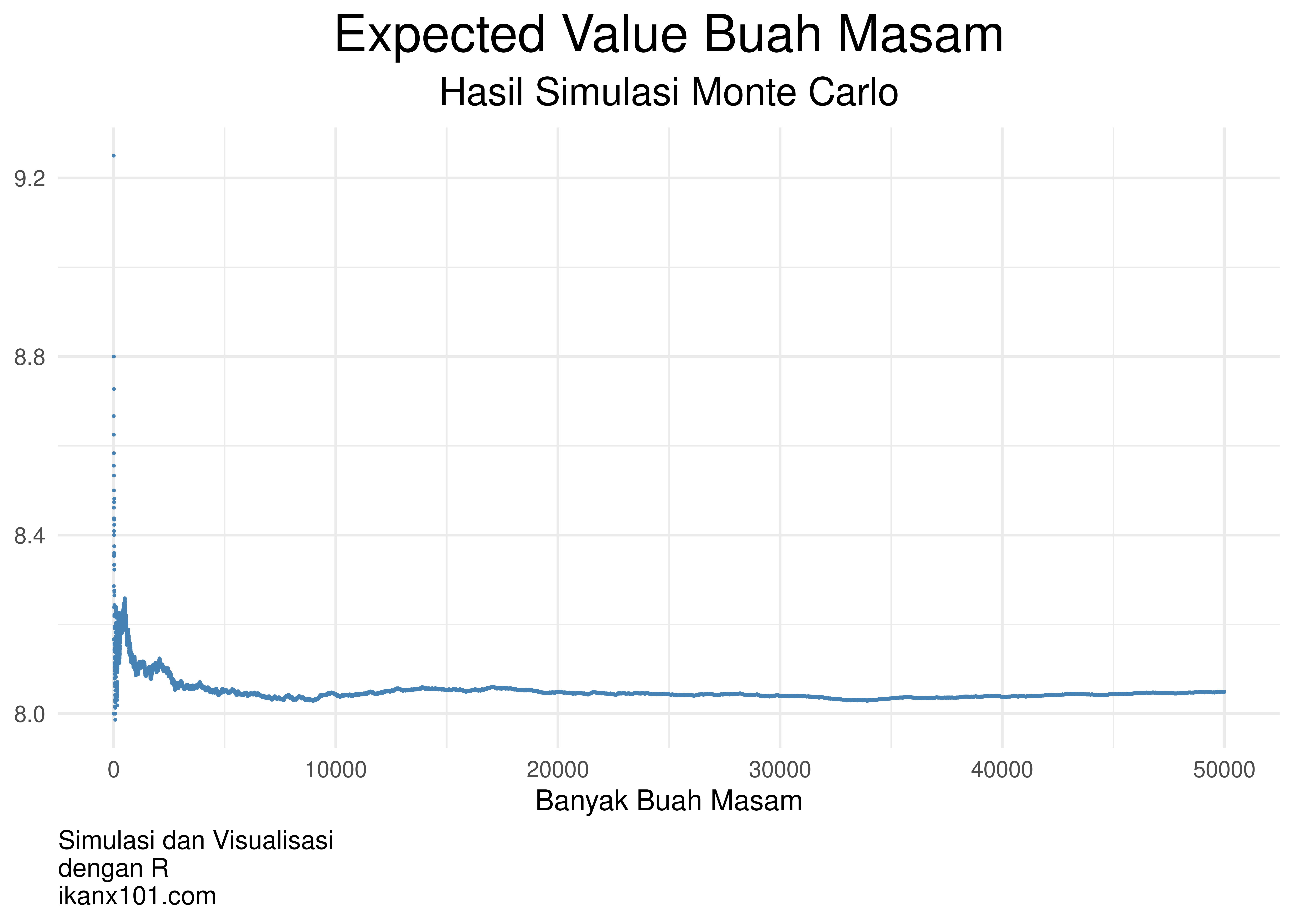
Terlihat dari grafik di atas, expected value buah masam yang didapatkan pelanggan adalah sekitar 8 buah.

---

Kira-kira seperti itu analogi dari kasus yang saya kerjakan.

if you find this article helpful, support this blog by clicking the ads.