Biaya Transport di Sekolah Baru si Sulung

Ceritanya di tahun ajaran baru, InsyaAllah si Sulung akan pindah sekolah. Dari sekolah lamanya yang relatif dekat rumah ke sekolah baru yang relatif jauh dari rumah (tapi lebih dekat ke kantor saya).

Bismillah, pikir saya.

Salah satu konsekuensi real dari perubahan ini adalah pos biaya transportasi sekolah menjadi lebih besar. Seharusnya seperti itu.

---

Kondisinya seperti ini:

Berangkat Sekolah

• Biasanya saya yang akan mengantar si Sulung.
  • Moda transportasi yang digunakan biasanya adalah motor. Tapi ada kondisi di mana saya harus ke Bogor, sehingga nantinya saya harus mengantarkannya menggunakan mobil (agar saya bisa langsung berangkat). Kondisi ini sebenarnya cukup jarang. Hanya sekali dari 20 hari kerja.
  • Hitungan kasar saya, motor menghabiskan Rp3.000 - Rp8.000
  • Sedangkan mobil, menghabiskan Rp10.000 - Rp20.000

Pulang Sekolah

• Biasanya nyonya yang akan menjemput si sulung dengan mobil. Tapi jika mobil saya bawa, terpaksa nyonya akan menggunakan jasa Go-Car atau Grab-Car untuk menjemputnya.
  • Hitungan dengan mobil, sekitar Rp15.000 - Rp25.000 (karena pp rumah - sekolah)
  • Hitungan dengan taksi online, sekitar Rp35.000 - Rp50.000

---

Berdasarkan informasi di atas, bisakah saya hitung berapa perkiraan biaya bulanan untuk antar jemput si Sulung?

Asumsi: sebulan adalah 20 hari kerja.

---

Simulasi Monte Carlo (lagi)

Entah kenapa saya sedang senang-senangnya melakukan simulasi ini. Kemampuannya dalam memperkirakan semua kemungkinan yang mungkin keluar menjadi kekuatan utamanya.

Oke, gak usah lama-lama, kita mulai simulasinya sebagai berikut:

Bikin fungsi biaya_bulanan

Saya mulai dengan membuat fungsi yang bisa menghitung berapa besar biaya bulanan dari kondisi-kondisi yang ada.

biaya_bulanan = function(){
saya_antar = sample(c(T,F),
                    20,
                    replace = T,
                    prob = c(19/20,1/20))
biaya_pagi = ifelse(saya_antar == T,
                    sample(c(3:8),1),
                    sample(c(10:20),1))

biaya_pagi = sum(biaya_pagi)


biaya_sore = ifelse(saya_antar == T,
                    sample(c(15:25),1),
                    sample(c(35:50),1))

biaya_sore = sum(biaya_sore)
biaya_sebulan = biaya_pagi + biaya_sore
return(biaya_sebulan)}

Lakukan simulasi dengan iterasi yang banyak

Sekarang kita lakukan prinsip Monte Carlo-nya:

# bikin fungsi simulasi
simulasi = function(iter){
  k = 1
  cost = c()
  for(i in 2:iter){
    temp = biaya_bulanan()
    cost = c(cost,temp)
  }
  return(mean(cost))
}

# saya akan iterasi sebanyak 2500 kali
result = data.frame(banyak_iterasi = c(3:2500))
result$biaya = sapply(result$banyak_iterasi,
                      simulasi)

# 10 hasil iterasi teratas
head(result,10)

##    banyak_iterasi    biaya
## 1               3 612.0000
## 2               4 539.0000
## 3               5 513.0000
## 4               6 615.6000
## 5               7 575.3333
## 6               8 524.8571
## 7               9 568.7500
## 8              10 568.0000
## 9              11 512.1000
## 10             12 563.5455

# 10 hasil iterasi terbawah
tail(result,10)

##      banyak_iterasi    biaya
## 2489           2491 540.9530
## 2490           2492 540.6118
## 2491           2493 545.4924
## 2492           2494 543.0221
## 2493           2495 544.5253
## 2494           2496 542.5170
## 2495           2497 541.3149
## 2496           2498 540.3428
## 2497           2499 543.8335
## 2498           2500 543.6723

Expected value biaya transportasi bulanan si sulung adalah sebesar: (dalam ribu rupiah)

## [1] 542.1168

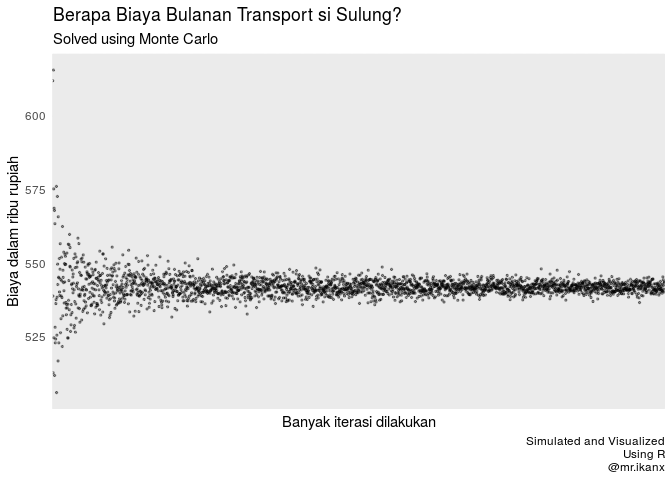
Jika kita lihat grafik di atas. semakin banyak saya melakukan iterasi, maka nilai hasil simulasinya akan konvergen ke satu nilai.

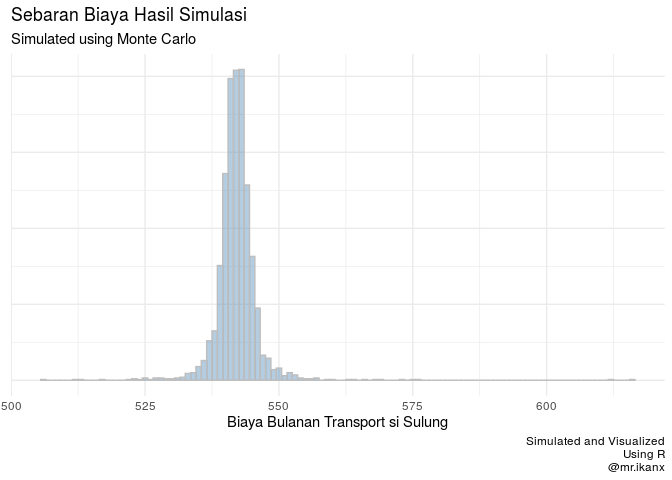
Oke, saya akan melakukan extra miles dengan melihat sebaran data biaya hasil simulasi.

Jadi hanya mengambil sumbu Y dari grafik di atas lalu membuat histogramnya.