Penjelasan Sederhana Tentang Beberapa Model Pada Teori Antrian

Mengantri itu adalah suatu aktivitas yang tidak kita senangi. Di satu sisi kita tidak ingin menunggu lama-lama namun di sisi lain kita ingin dilayani secara ramah, prima, dan baik.

Setiap kali mengantri di suatu tempat, saya selalu bertanya-tanya:

1. Berapa lama saya harus mengantri?
2. Berapa banyak orang yang mengantri?
3. Apa yang terjadi jika ada jalur antrian baru yang dibuka?

---

Pertanyaan-pertanyaan tersebut membuat saya teringat salah satu topik yang dulu sempat dibahas saat kuliah di matematika, yakni: teori antrian. Sayang sekali saya tidak mengambil mata kuliah tersebut tapi kali ini saya akan mencoba membahasnya tipis-tipis di blog ini.

Queueing Theory: Matematika di Balik Antrian

Queueing theory adalah cabang matematika terapan yang mempelajari aliran antrian, digunakan di supermarket, bandara, hingga jaringan komputer. Tujuannya adalah untuk menganalisis dan mengoptimalkan sistem antrian agar lebih efisien.

Beberapa konsep kunci dalam teori antrian bisa dituliskan sebagai berikut:

• Kedatangan (Arrival Rate - ): Rata-rata banyaknya orang yang masuk antrian pada rentang waktu tertentu.
  • Arrival rate mengikuti distribusi Poisson.
• Layanan (Service Rate - ): Rata-rata banyaknya orang yang dilayani per rentang waktu tertentu.
  • Nilai ini tidak terbatas pada distribusi tertentu.
  • Bisa jadi bernilai konstan atau dinamis mengikuti distribusi tertentu.
• Jumlah pelayan (servers): Berapa banyak pelayan yang bertugas.
  • Suatu sistem antrian bisa memiliki satu atau banyak server (single server / multi server).
• Intensitas traffic antrian (): Merupakan rasio dari arrival rate dan service rate.
  • Dituliskan secara matematis .
  • Nilai ini menentukan seberapa padat sistem antrian.
  • Jika , sistem antrian akan stabil (antrian akan terbatas).
  • Jika , sistem antrian akan terus memanjang tak terbatas.
• Variabilitas (): Ketidakpastian dalam waktu pelayanan (misal: ada konsumen yang membayar menggunakan uang koin sehingga membutuhkan waktu lebih lama).

Sekarang berbekal konsep kunci tersebut, mari kita telaah sistem antrian berdasarkan beberapa model berikut ini:

Model I - Model Antrian Sederhana (M/M/1)

Model M/M/1 menggambarkan situasi antrian saat hanya ada satu server yang bertugas melayani semua orang yang datang.

• “M” = Kedatangan pelanggan acak (Poisson). Nilainya mengikuti distribusi Poisson dengan tingkat kedatangan .
• “M” = Waktu pelayanan. Mengikuti distribusi eksponensial dengan tingkat pelayanan .
• “1” = 1 server.

Misalkan suatu minimarket yang buka selama 15 jam hanya memiliki satu kasir dengan:

1. Tingkat kedatangan pelanggan: 5 pelanggan per jam ().
2. Tingkat pelayanan: 8 pelanggan per jam ().

Dari parameter di atas, kita bisa menghitung intensitas traffic antrian sebagai berikut:

Kita bisa menyimpulkan bahwa sistem antrian akan stabil. Saya akan simulasikan antrian yang terjadi selama satu minggu (15 jam x 7 hari) di minimarket tersebut.

# Simulasi Antrian M/M/1

# Parameter
lambda   = 5     # Tingkat kedatangan (pelanggan per jam)
mu       = 8     # Tingkat pelayanan (pelanggan per jam)
sim_time = 15*7  # Waktu simulasi (jam)

Hasil Simulasi:

Rata-rata panjang antrian: 1.520439 

Utilisasi server (ρ simulasi): 0.782652 

Hasil Teoritis (M/M/1):

Faktor utilisasi (ρ): 0.625 

Jumlah pelanggan rata-rata dalam sistem (L): 1.666667 

Waktu rata-rata dalam sistem (W): 0.3333333 jam atau 20 menit

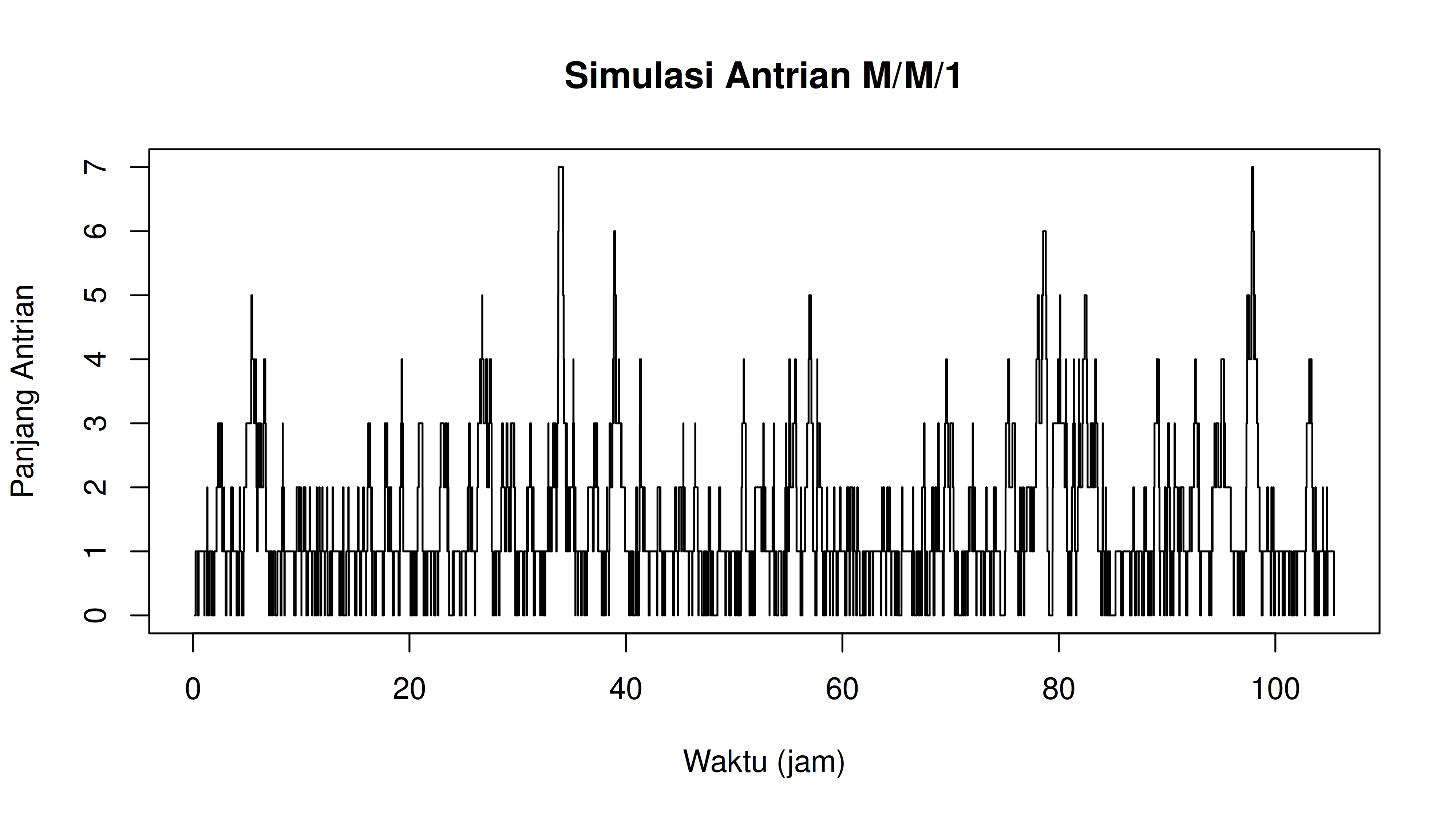
Kita bisa lihat dari simulasi tersebut bahwa kasir minimarket bisa memberikan layanan antrian yang terkendali. Walaupun sempat terjadi antrian panjang di rentang waktu tertentu tapi tak akan membengkak semakin besar.

Apa yang terjadi jika nilai ?

Coba kita simulasikan kembali:

# Simulasi Antrian M/M/1

# Parameter
lambda   = 5     # Tingkat kedatangan (pelanggan per jam)
mu       = 5     # Tingkat pelayanan (pelanggan per jam)
sim_time = 15*7  # Waktu simulasi (jam)

Hasil Simulasi:

Rata-rata panjang antrian: 11.12821 

Utilisasi server (ρ simulasi): 0.9924027 

Hasil Teoritis (M/M/1):

Faktor utilisasi (ρ): 1 

Jumlah pelanggan rata-rata dalam sistem (L): Inf 

Waktu rata-rata dalam sistem (W): Inf jam atau Inf menit

Terlihat bahwa antrian akan selalu ada dan tak ada tanda-tanda pelanggan akan selesai dilayani.

Sekarang saya akan eksplor sistem antrian lain saat ada multiple server.

Model II - Model Antrian Multiple Server (M/M/c)

Model M/M/c menggambarkan situasi antrian saat ada satu antrian tunggal yang dialirkan ke multiple server. Asumsi dasar dari model ini adalah tingkat pelayanan setiap server adalah sama (konsisten antar server).

Kita akan simulasikan sistem antrian di minimarket tadi jika ada tiga kasir yang melayani konsumen. Agar menarik, kita akan buat skenario seperti ini:

Skenario I: Underload yakni sumber daya berlebih, tapi minimarket sepi.

• Tingkat kedatangan pelanggan rendah 0.1 pelanggan per jam ().
• Ada sepuluh kasir dengan tingkat pelayanan masing-masing 10 pelanggan per jam ().

Total customers:
 5000
Missed customers:
 0
Mean waiting time:
 -4.7e-14
Mean response time:
 0.0999
Utilization factor:
 0.000990298398017608
Mean queue length:
 9.92e-12
Mean number of customers in system:
 0.0099

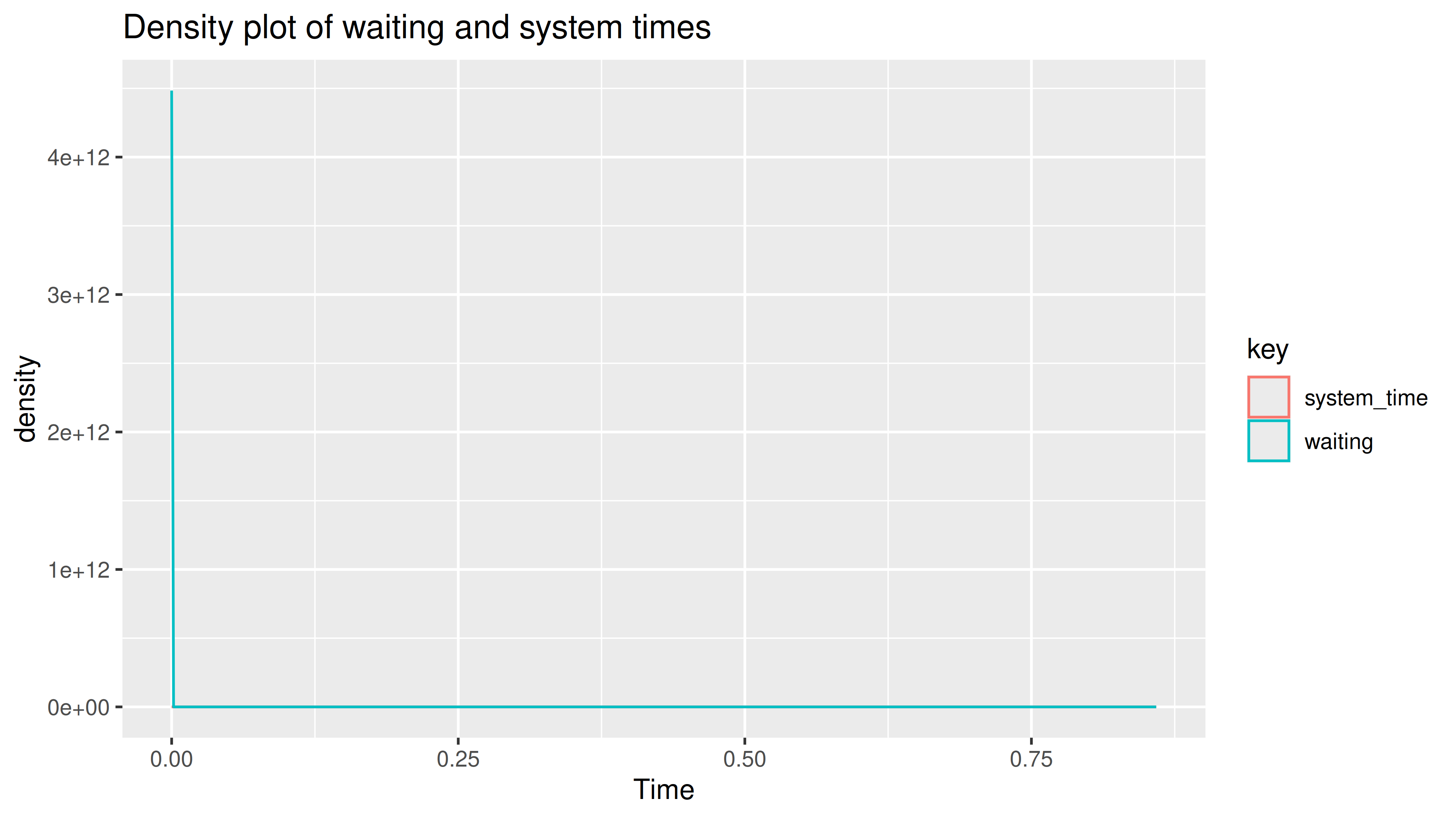
Hasilnya adalah sistem antrian selalu kosong. Hampir tidak ada antrian yang terbentuk.

Skenario II: Overload yakni sumber daya terbatas, minimarket ramai, dan server lamban.

• Tingkat kedatangan pelanggan tinggi 20 pelanggan per jam ().
• Ada dua kasir dengan tingkat pelayanan masing-masing 1 pelanggan per jam ().

Total customers:
 5000
Missed customers:
 0
Mean waiting time:
 1110
Mean response time:
 1120
Utilization factor:
 0.99951882209991
Mean queue length:
 2230
Mean number of customers in system:
 2230

Hasilnya adalah antrian tumbuh tak terbatas, waktu tunggu semakin lama, semua server selalu sibuk, dan sistem tidak stabil.

Skenario III: Critical load yakni sistem antrian berada di batas stabilitas.

• Tingkat kedatangan pelanggan 5 pelanggan per jam ().
• Ada lima kasir dengan tingkat pelayanan masing-masing 1 pelanggan per jam ().

Total customers:
 5000
Missed customers:
 0
Mean waiting time:
 4.29
Mean response time:
 5.29
Utilization factor:
 0.9815705615255
Mean queue length:
 21.1
Mean number of customers in system:
 26

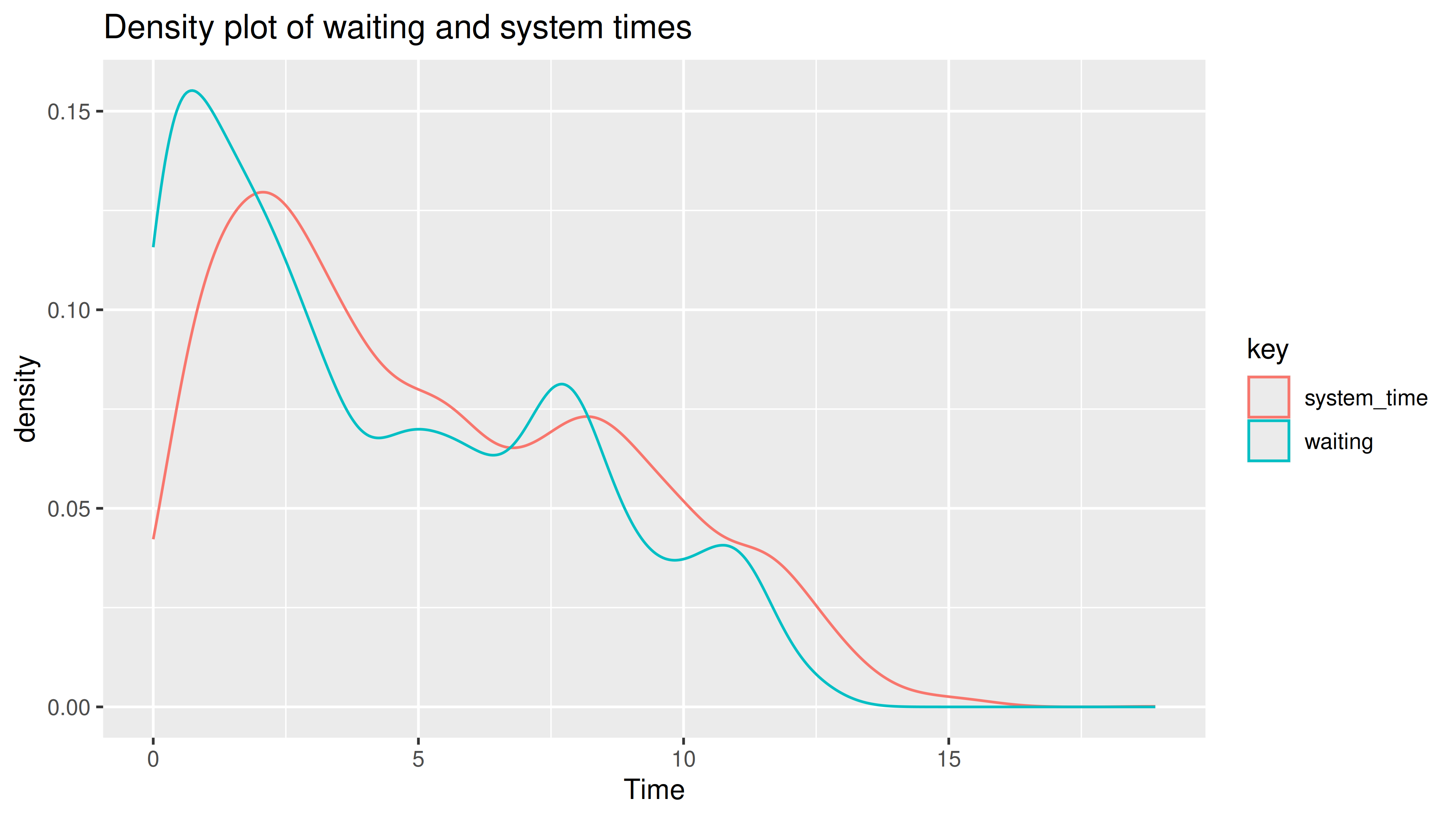
Berikut adalah komparasi ketiga skenarionya:

   Scenario Mean.Waiting.Time Mean.Queue.Length Utilization
1 Underload               0.0                 0       0.001
2  Overload           1 114.7             2 234       1.000
3  Critical               4.3                21       0.982

Masih ada beberapa model lagi yang bisa kita eksplor, jadi stay tuned ya.

Model III - Model Antrian General Multiple Server (M/G/c)

Model kedua di atas tidak memperhitungkan variasi yang terjadi antar layanan server. Karena server juga manusia yang kadang bisa cepat atau lambat. Model M/G/c adalah model antrian dengan karakteristik:

1. Kedatangan (M): Mengikuti proses Poisson dengan tingkat .
2. Pelayanan (G): Waktu pelayanan mengikuti distribusi umum (General) dengan mean: dan variansi .
3. server: Terdapat server paralel.

Perbedaan utama dengan M/M/c:

• M/M/c mengasumsikan waktu pelayanan eksponensial
• M/G/c lebih fleksibel dengan berbagai distribusi waktu pelayanan (normal, uniform, konstan, atau lainnya).

Contoh Aplikasi M/G/c:

1. Bandara (Check-in Counter):
   • Kedatangan penumpang: Poisson.
   • Waktu pelayanan: Distribusi normal (karena proses check-in relatif konsisten).
   • Banyak counter paralel.
2. Rumah Sakit (IGD):
   • Kedatangan pasien: Acak (Poisson).
   • Waktu pelayanan: Distribusi Weibull (beberapa kasus cepat, beberapa lama).
   • Beberapa dokter jaga.
3. Call Center:
   • Panggilan masuk: Poisson.
   • Durasi panggilan: Distribusi log-normal (banyak panggilan singkat, beberapa sangat panjang).
   • Banyak operator.

Berikut adalah contoh simulasi saat parameter:

1. , tingkat kedatangan (pelanggan/jam).
2. , tingkat pelayanan rata-rata (pelanggan/jam per server).
3. , variasi pelayanan.
4. , jumlah server.

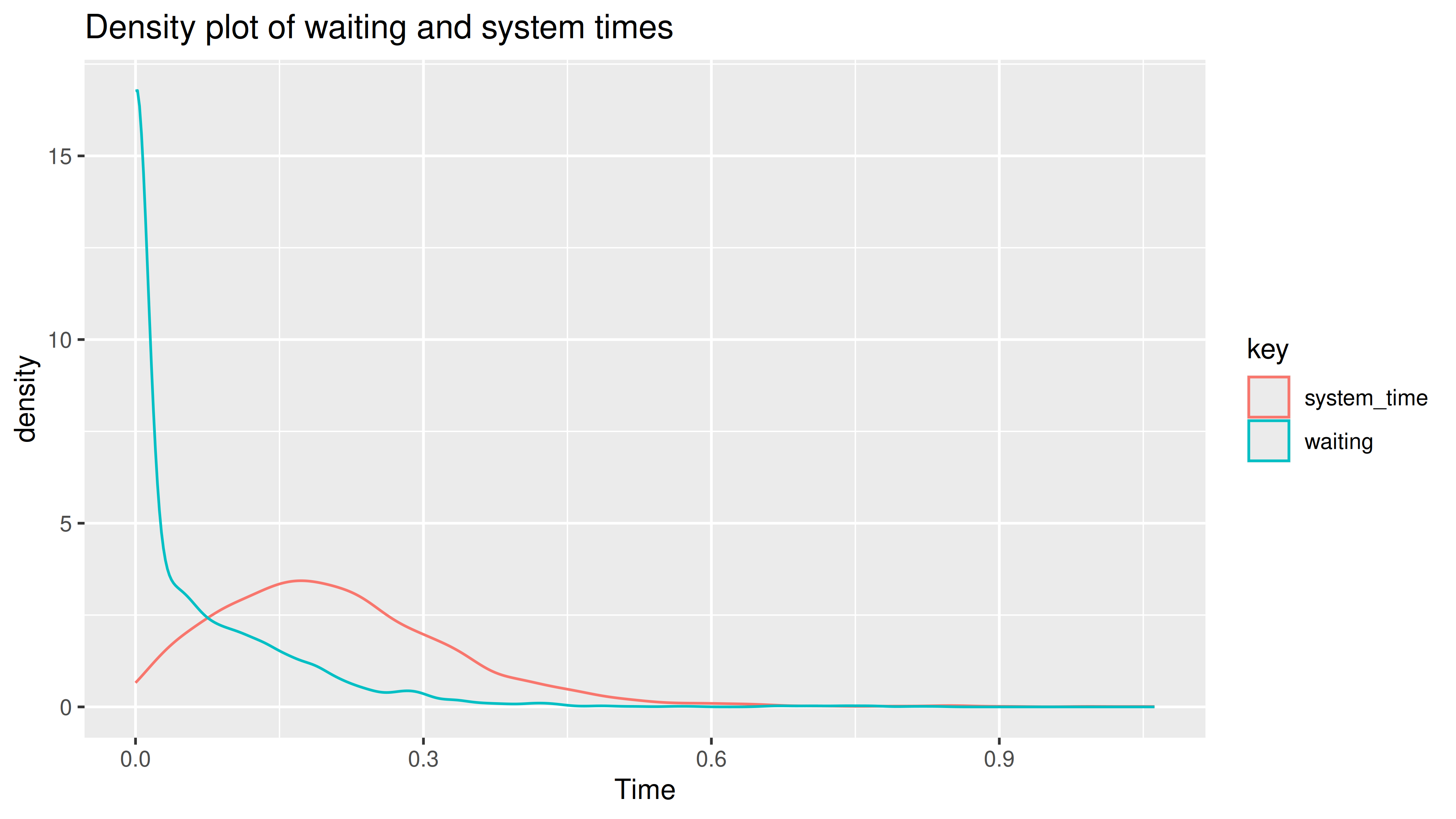
Total customers:
 3000
Missed customers:
 0
Mean waiting time:
 0.0596
Mean response time:
 0.21
Utilization factor:
 0.730933840247701
Mean queue length:
 0.87
Mean number of customers in system:
 3.06

Model IV - Model Antrian General Multiple Server with Capacity (M/G/c/K)

Model terakhir yang hendak saya bahas adalah pengembangan dari model sebelumnya. Salah satu pengembangan kuncinya adalah adanya kapasitas dari sistem antrian. Model M/G/c/K adalah model antrian yang lebih realistis dengan karakteristik:

1. Kedatangan (M): Mengikuti proses Poisson dengan tingkat .
2. Pelayanan (G): Waktu pelayanan mengikuti distribusi umum (General) dengan mean: dan variansi .
3. server: Terdapat server paralel.
4. Kapasitas (K): Kapasitas sistem terbatas (antrian + pelayanan ≤ K).

Perbedaan utama dengan M/G/c:

• M/G/c/K memiliki kapasitas terbatas (K).
• Pelanggan yang datang saat sistem penuh akan ditolak/dibuang (blocked).

Contoh Aplikasi M/G/c/K:

1. Call Center dengan Antrian Terbatas:
   • Maksimal 20 panggilan dalam sistem (15 menunggu + 5 sedang dilayani).
   • Panggilan baru ditolak jika sistem penuh.
2. Parkir Mobil:
   • Kapasitas 50 mobil.
   • Kedatangan acak, waktu parkir bervariasi.
   • Mobil ditolak jika parkir penuh.
3. Sistem ICU Rumah Sakit:
   • 10 tempat tidur ICU.
   • Kedatangan pasien emergensi acak.
   • Lama perawatan bervariasi.
   • Pasien dirujuk ke rumah sakit lain jika ICU penuh.

Sekarang kita akan lakukan simulasi dengan parameter berikut:

Berikut adalah contoh simulasi saat parameter:

1. , tingkat kedatangan (pelanggan/jam).
2. , tingkat pelayanan rata-rata (pelanggan/jam per server).
3. , variasi pelayanan.
4. , jumlah server.
5. , kapasitas sistem antrian.

=== Hasil Simulasi M/G/2/5 dengan simmer ===

Total kedatangan: 782 

Total dilayani: 774 

Total blocked: 8 

Probabilitas blocking: 0.01 

Rata-rata waktu tunggu: 0.061 jam

Rata-rata panjang antrian: 0.38 

Utilisasi server: 0.668 

---

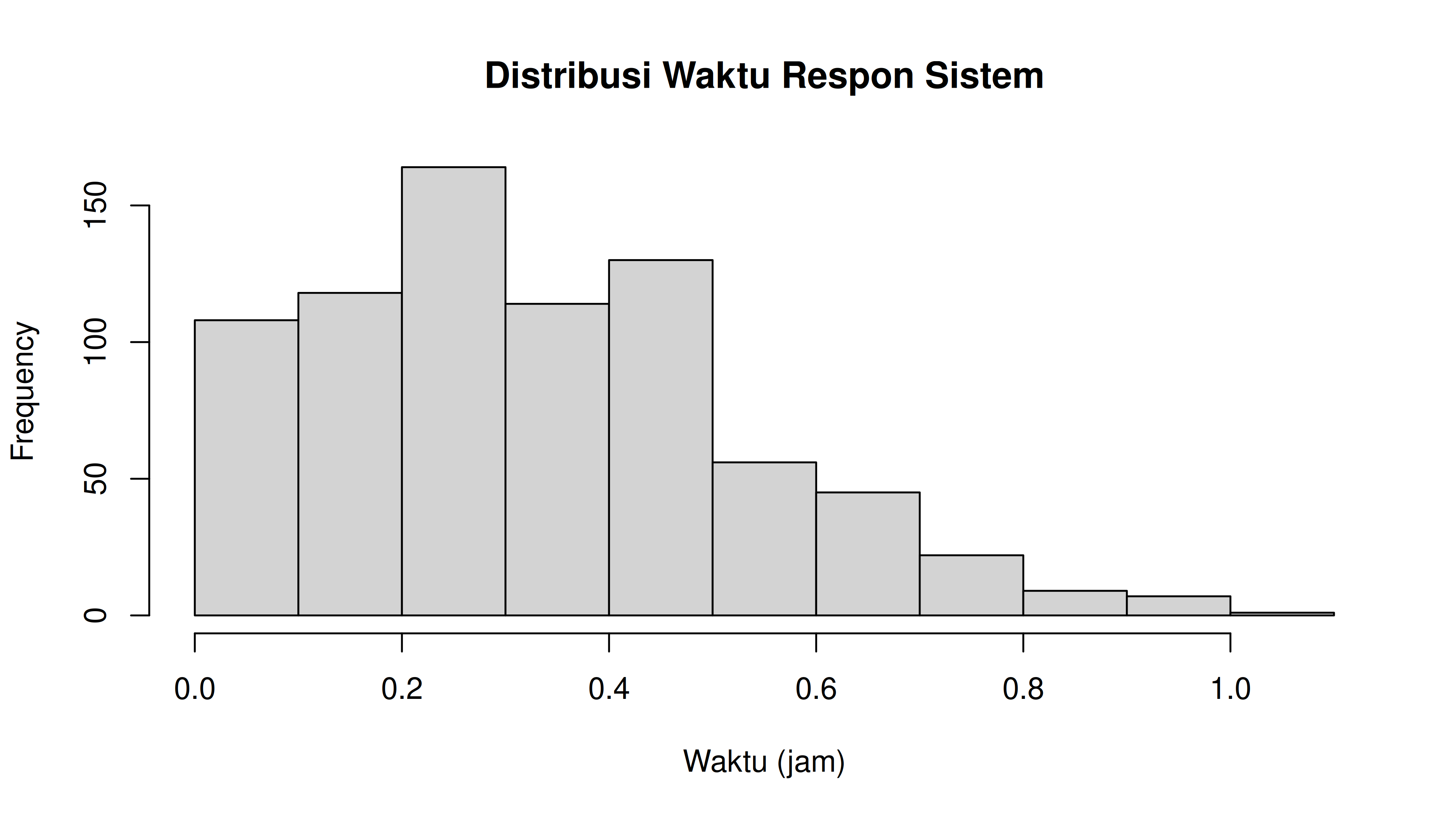
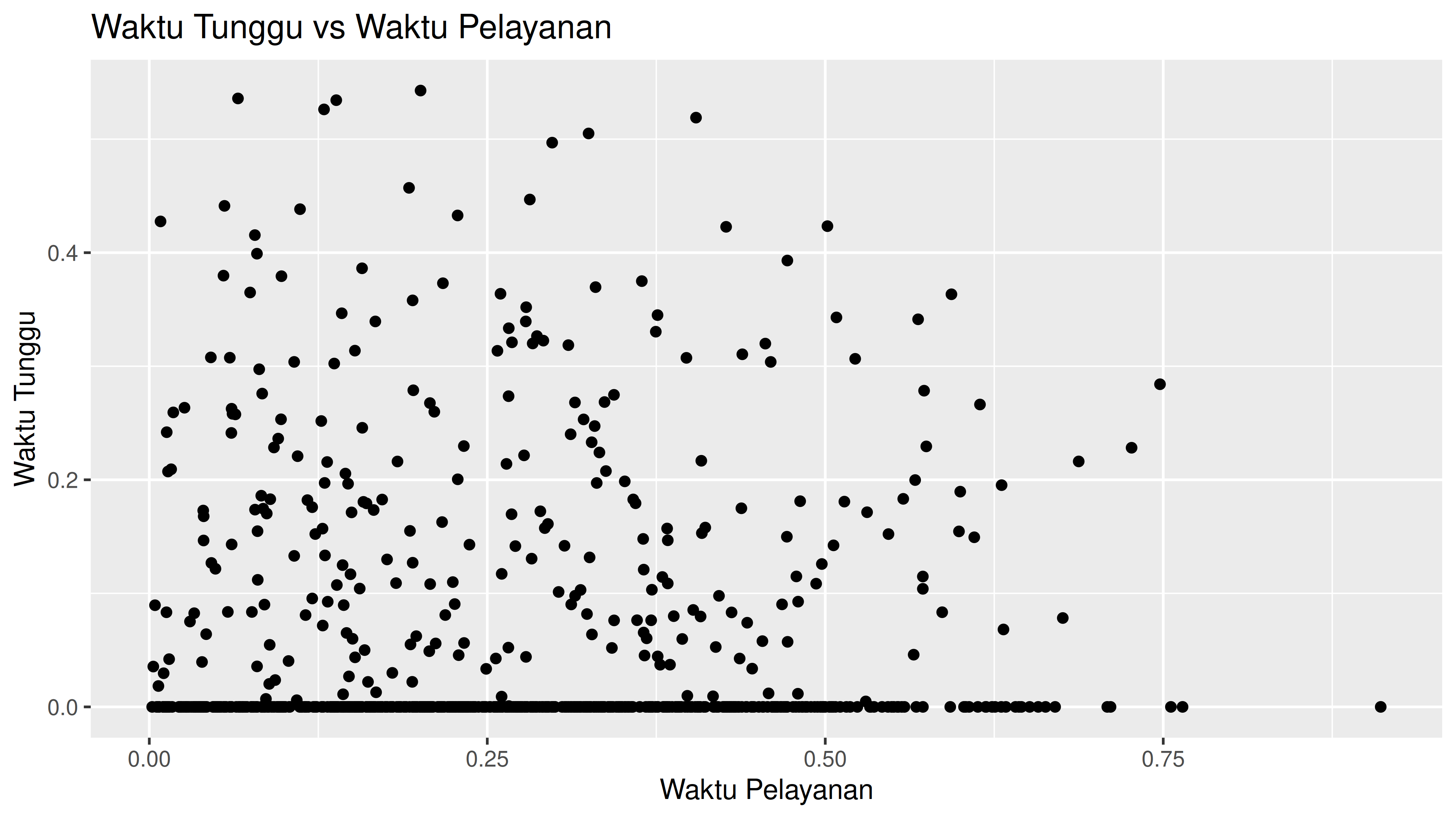
Apa faedahnya jika kita bisa memodelkan sistem antrian dengan teori antrian? Kita bisa melakukan beberapa hal berikut ini:

1. Optimasi Biaya Operasional

• Contoh: Supermarket menentukan jumlah optimal kasir.
• Manfaat:
  • Menyeimbangkan biaya server (kasir/staf) vs biaya antrian (customer dissatisfaction)
  • Mengidentifikasi titik optimal dimana penambahan server tidak lagi ekonomis
  • Studi kasus: Call center mengurangi 15% biaya operasional dengan model M/M/c

2. Peningkatan Kepuasan Pelanggan

• Metric: Waktu tunggu (Wq) dan panjang antrian (Lq)
• Aplikasi:
  • Restoran cepat saji mengatur jadwal karyawan berdasarkan prediksi antrian
  • Rumah sakit mengurangi waktu tunggu pasien IGD dari 60 menit menjadi 25 menit
• Data: Setiap 10% penurunan waktu tunggu meningkatkan NPS 5 poin (retail)

3. Manajemen Kapasitas yang Data-Driven

• Tools: Model M/M/c/K untuk sistem kapasitas terbatas
• Implementasi:
  • Parkir mal dengan 200 slot → model menentukan 95% probability tersedia slot
  • Bandara mengoptimalkan security check lanes
• Impact: Mengurangi lost sales 20% pada peak hours

Teori antrian memberikan framework kuantitatif untuk:

• Mengkonversi customer pain points (antrian) ke metrik terukur
• Mengevaluasi ROI penambahan sumber daya
• Membuat keputusan berbasis data bukan asumsi
• Memprediksi perilaku sistem dibawah berbagai kondisi

---

if you find this article helpful, support this blog by clicking the ads.