Tugas/Ujian Sains Komputasi: Algoritma dan Perancangan Software - Tugas I
Saya memutuskan untuk membuat satu kategori baru di blog saya, yakni: pembahasan soal dan ujian di Sains Komputasi ITB saat saya kuliah beberapa saat lalu. Pada tulisan yang pertama ini, saya akan membahas tugas pertama yang sayadapatkan saat masuk magister di Sains Komputasi, yakni dari mata kuliah Algorithm and Software Design.
Cekidot!
TASK 1
Soal
Construct a flowchat to solve factorial problem!
Jawab
Untuk memudahkan pembuatan algoritma, kita akan melihat kembali definisi dari faktorial sebagai berikut:
Dengan syarat
dan
berupa integer.
Namun perlu diperhatikan bahwa
.
Oleh karena itu, kita bisa menggunakan prinsip rekursif dengan algoritma dalam pseudocode berikut ini:
Algoritma dalam Pseudocode
INPUT n
IF n NOT INTEGER OR n < 0 STOP
IF n = 0 OR n = 1 RETURN 1
ELSE
DEFINE a = 1
FOR i 2:n
a = a*i
RETURN a
Bentuk flowchart dari pseudocode di atas adalah sebagai berikut:
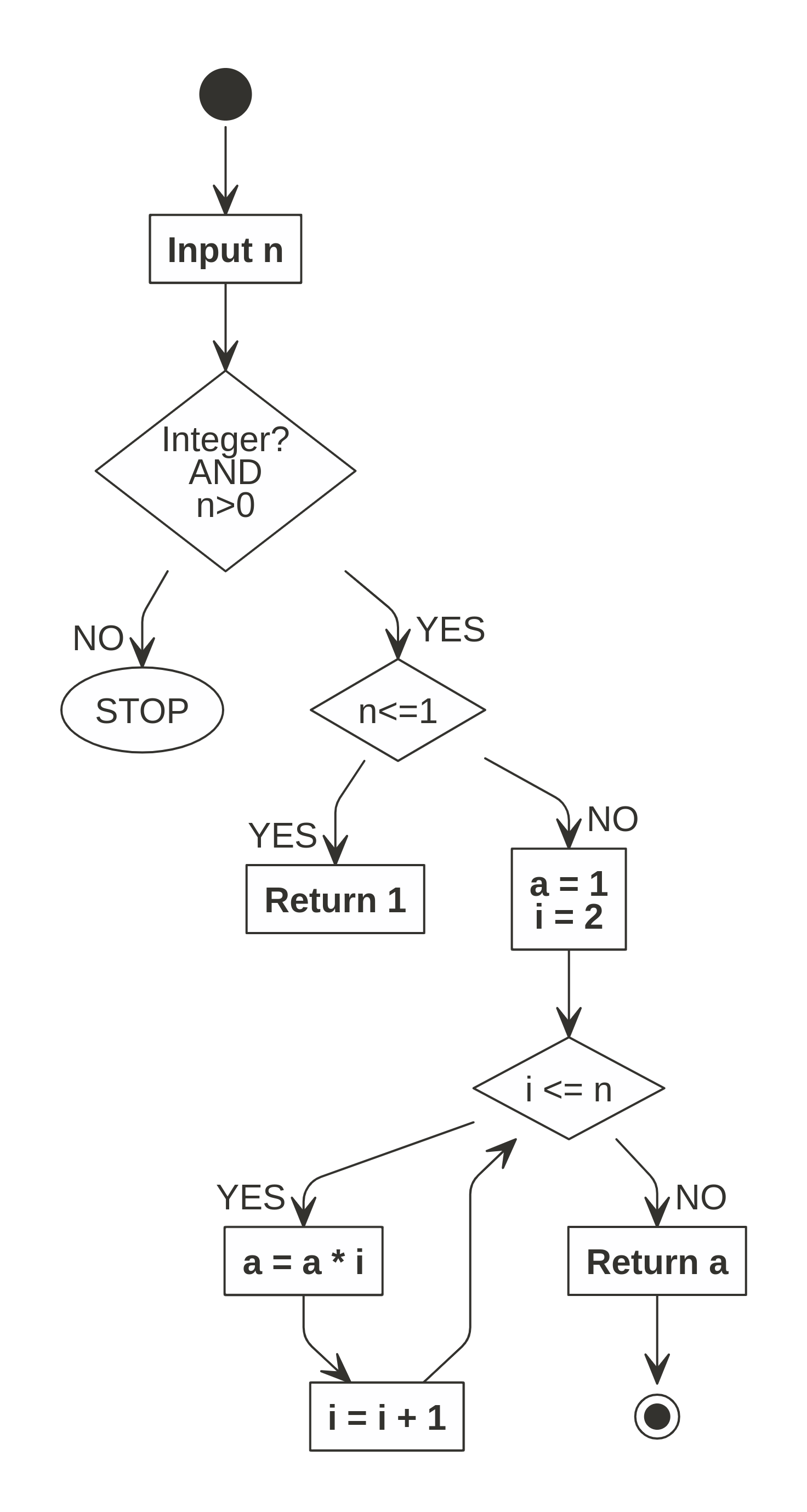
Flowchart Faktorial
R function
Sekarang algoritma di atas jika dibuat R function-nya adalah sebagai berikut:
f_torial = function(n){
# initial definition
hasil = 1
# conditional
if(n < 0){hasil = "n yang dimasukkan < 0"}
else if(n %in% c(0,1)){hasil = 1}
else{
for(i in 2:n){
hasil = hasil*i
}
}
# return output perhitungan
output = list(
`Input angka` = n,
`n!` = hasil
)
# print output
return(output)
}
Mari kita cek hasilnya dalam berbagai kondisi berikut:
f_torial(-2)
## $`Input angka`
## [1] -2
##
## $`n!`
## [1] "n yang dimasukkan < 0"
f_torial(0)
## $`Input angka`
## [1] 0
##
## $`n!`
## [1] 1
f_torial(1)
## $`Input angka`
## [1] 1
##
## $`n!`
## [1] 1
f_torial(4)
## $`Input angka`
## [1] 4
##
## $`n!`
## [1] 24
f_torial(7)
## $`Input angka`
## [1] 7
##
## $`n!`
## [1] 5040
f_torial(10)
## $`Input angka`
## [1] 10
##
## $`n!`
## [1] 3628800
TASK 2
Soal
Construct Pascal’s triangle!
Jawab
Segitiga pascal adalah “segitiga” yang barisnya dibangun dari penambahan baris di atasnya (dengan baris teratas adalah bilangan 1). Berikut adalah ilustrasinya:

Pascal Triangle
Bagaimana cara membuatnya?
- Baris
1berisi bilangan 1. - Baris
2berisi barisan bilangan dengan2elemen. Isinya adalah baris1di kanan dan kirinya. - Baris
3berisi barisan bilangan dengan3elemen. Isinya adalah baris2setelah kita tambahkan elemen baru di kanan dan kirinya. - Baris
nberisi barisan bilangan dengannelemen. Isinya adalah barisn-1setelah kita tambahkan elemen baru di kanan dan kirinya.
Algoritma dalam Pseudocode
INPUT n
x = 1
FOR i 2:n
x = (0,x) + (x,0)
OUTPUT x
R function
Berikut adalah fungsinya jika dibuat di R:
pascal = function(n){
# initial
x = 1
print(x)
for(i in 2:n){
x = c(0,x) + c(x,0)
print(x)
}
}
Mari kita coba dengan beberapa nilai:
pascal(4)
## [1] 1
## [1] 1 1
## [1] 1 2 1
## [1] 1 3 3 1
pascal(8)
## [1] 1
## [1] 1 1
## [1] 1 2 1
## [1] 1 3 3 1
## [1] 1 4 6 4 1
## [1] 1 5 10 10 5 1
## [1] 1 6 15 20 15 6 1
## [1] 1 7 21 35 35 21 7 1
